想通过石墨烯重新学习一下拓扑,以此来记录学习成果。
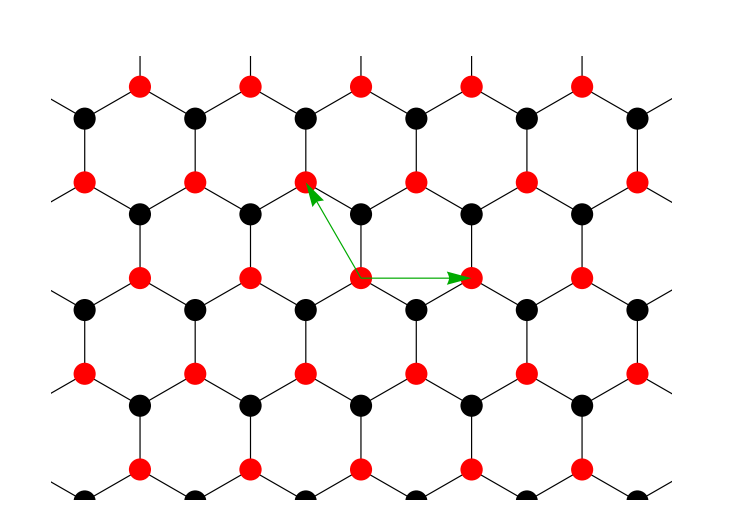
石墨烯的结构
石墨烯的元胞是六角蜂窝状的,它的基元包含两个原子,将红黑表示的位置放在一起,则表示它的一个基元。以水平和垂直方向建立直角坐标系,并将它的晶格常数(红黑位置的距离)设置为a,基矢为绿色箭头表示$\vec{v_1}=(\sqrt{3}a,0),\vec{v_2}=(-\sqrt{3}/2a,3/2a)$。若只考虑最紧邻位置间的hopping,那么实空间中的Hamiltonian为
\[H=-t\sum_{<i,j>}a_i^\dagger b_j - t\sum_{<i,j>}b_i^\dagger a_j\]$<i,j>$表示的是格点上最近邻的位置。先忘记上面说过的基元的概念,同时忽略图中黑红位置的区别,将所有的格点位置视为相同,那么可以发现每个格点都是有三个最近邻的,这就是石墨烯六角结构和平时经常使用正方点阵的一个区别,正方点阵每个格点都是有四个最近邻的(上下左右,而且它们是相互垂直的),石墨烯结构中则不然,三个最近邻位置的夹角是$120^o$,这三个最近邻的矢量表示为
\[\vec{e_1}=(0,a)\quad \vec{e_2}=(-\frac{\sqrt{3}}{2}a,-\frac{a}{2})\quad\vec{e_3}=(\frac{\sqrt{3}}{2}a,-\frac{a}{2})\]最近邻的三个基矢确定时候,可以将上面的Hamiltonian写成更加具体的一个形式
\[H=-t\sum_ia_\vec{r_i}^\dagger b_{\vec{r_i}+\vec{e_1}}-t\sum_ia_\vec{r_i}^\dagger b_{\vec{r_i}+\vec{e_2}}-t\sum_ia_\vec{r_i}^\dagger b_{\vec{r_i}+\vec{e_3}}+h.c\](h.c是前半部分的厄密共轭)
同样的,实空间格点上的算符,可以通过Fourier变换,变换到k空间,反过来也是可以的,变换关系为
\[a_k=\frac{1}{\sqrt{N}}\sum_ja_je^{i\vec{k}\cdot\vec{r} }\quad a_j=\frac{1}{\sqrt{N}}\sum_ka_ke^{-i\vec{k}\cdot\vec{r}}\] \[b_k=\frac{1}{\sqrt{N}}\sum_jb_je^{i\vec{k}\cdot\vec{r} }\quad b_j=\frac{1}{\sqrt{N}}\sum_kb_ke^{-i\vec{k}\cdot\vec{r}}\]利用这个变换关系式,可以将实空间的算符形式变换到k空间
\[-t\sum_ja_{\vec{r_j}}^\dagger b_{\vec{r_j}+\vec{e_1}}=-\frac{t}{N}\sum_j\sum_k\sum_{k'}a_k^\dagger e^{i\vec{k}\cdot\vec{r_j}}b_{k'}e^{-i\vec{k'}\cdot(\vec{r_j}+\vec{e_1})}=-t\sum_k\sum_{k'}a_k^\dagger b_{k'}e^{-i\vec{k'}\cdot\vec{e_1}}\frac{1}{N}\sum_je^{i(\vec{k}-\vec{k'})\cdot\vec{r_j}}\]利用$\delta$函数的关系:$\delta_{k,k’}=\frac{1}{N}\sum_je^{i(\vec{k}-\vec{k’})\cdot\vec{r_j}}$
上面的关系式可以化简为
\[-t\sum_k\sum_{k'}a_k^\dagger b_{k'}e^{-i\vec{k'}\cdot\vec{e_1}}\delta_{k.k'}=-t\sum_ka_k^\dagger b_ke^{-i\vec{k}\cdot{e_1}}\]其他部分的变化也完全相同,最后可以将实空间的Hamiltonian变换到动量空间
\[H=-t\sum_ka_k^\dagger b_k(e^{i\vec{k}\cdot\vec{e_1}}+e^{i\vec{k}\cdot\vec{e_2}}+e^{i\vec{k}\cdot\vec{e_3}})-t\sum_kb_k^\dagger a_k(e^{-i\vec{k}\cdot\vec{e_1}}+e^{-i\vec{k}\cdot\vec{e_2}}+e^{-i\vec{k}\cdot\vec{e_3}})\]以$a_k$和$b_k$为基矢,可以将这个k空间中的Hamiltonian写成一个2*2的矩阵形式,之后就可以通过对角化的方式求的H(k)的本征矢和本征值。
石墨烯Zigzag边界态计算
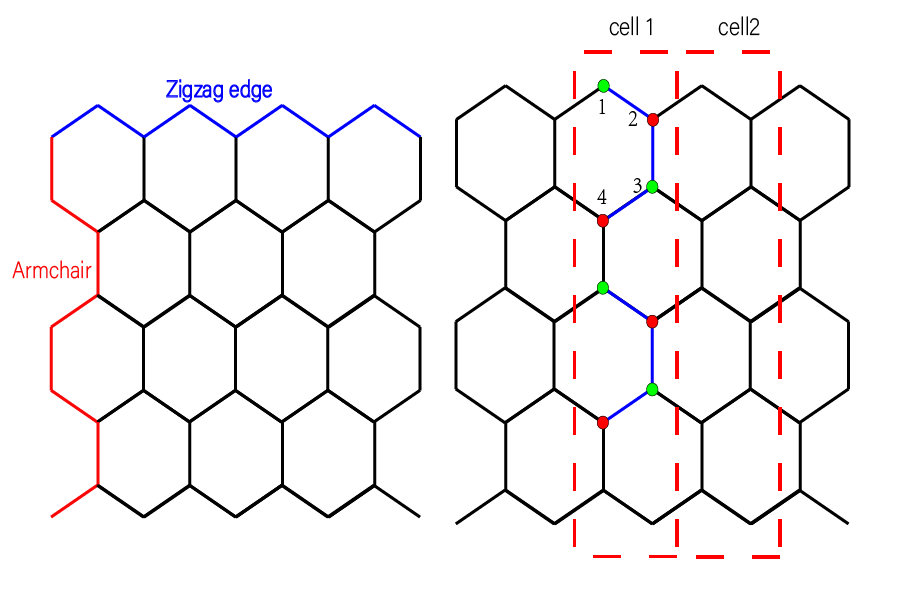
Graphene是个六角蜂窝状结构,它有两种边界:armchair和zigzag边界,如上图所示。以水平方向为x轴,竖直方向为y轴建立直角坐标系后,现在沿x方向取周期边界,y方向是开边界后,剩余的是一个zigzag边界,将哈密顿量沿x方向取周期,y方向取开边界则可以得到zigzag边界态。
右侧图中虚线框所示的是一个元胞,图中共框选出了两个“cell”,在一个cell中,沿y方向是开边界的,为了更方便的构造哈密顿量,再将一个cell的内部,分割成一些更小的重复单元,这些重复单元可以通过平移的方式组成这个基本的cell,入右图中蓝色标记所示,同时在每个位置上用一个数字来进行标记。将有编号的蓝色部分,沿y方向进行平移之后,就可以得到另外一个蓝色的重复结构。
在一个cell中,考虑最近邻格点之间的跃迁;先从一个cell中最小的重复结构来构建矩阵元(1<->2,2<->3,3<->4),这样cell内重复结构就可以完全构建,但是遗漏了这些重复结构之间的hopping(4<->5),所以在最后还需要将这个最小重复结构之间的hopping同样考虑进去;
在考虑完同一个cell内的情况之后,开始考虑cell之间的hopping(仅考虑最近零之间的hopping),同样以一个cell中的重复结构为基础,相邻元胞间(2<->1,3<->4)是满足条件的最近邻hopping,小的重复结构之中再没有满足相邻元胞之间最近邻hopping的点,所有的考虑到此结束
将上面考虑到的内容综合到一起之后,就可以得到在仅考虑最近邻hopping时Graphene的整个哈密顿量(x方向为周期边界,y方向为开边界)
clear;clc;
global N len t m0
N = 40;%一个元胞内的重复结构的数目
len = 4*N;
t = 1.0;
m0 = 0;
dlist = 300;
val = zeros(len,dlist);
klist = linspace(-2*pi,2*pi,dlist);
for i = 1:length(klist)
ham = f1(klist(i));
val(:,i) = eig(ham);
end
plot(klist,val)
xlabel('k_y')
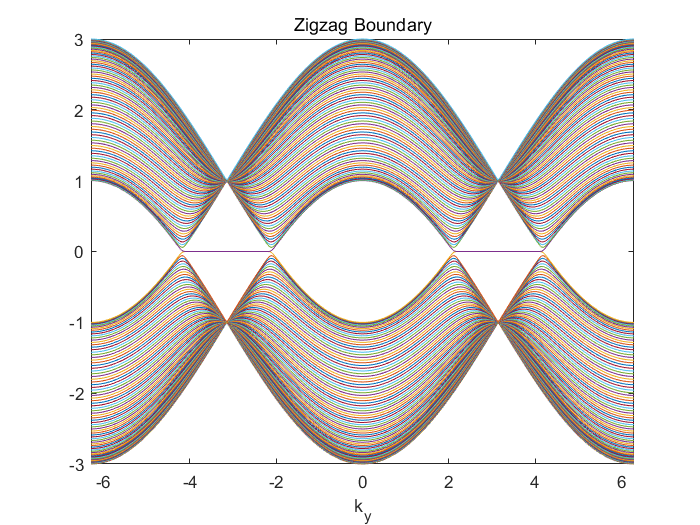
title('Zigzag Boundary')
axis([-2*pi 2*pi -3*t 3*t])
function ham = f1(kx)
global N t m0 len
ham = zeros(len,len);
for m = 0:N-1
% on-site mass term
ham(m*4+1,m*4+1) = m0;
ham(m*4+2,m*4+2) = -m0;
ham(m*4+3,m*4+3) = m0;
ham(m*4+4,m*4+4) = -m0;
% intra-cell hopping
%在实际考虑中可以将整个元胞当作一个压平的线,这样intra-cell就不用涉及到位相问题
%虽然从图形上看他们确实有不同的取向
ham(m*4+1,m*4+2) = t;
ham(m*4+2,m*4+1) = t;
ham(m*4+2,m*4+3) = t;
ham(m*4+3,m*4+2) = t;
ham(m*4+3,m*4+4) = t;
ham(m*4+4,m*4+3) = t;
end
for m = 1:N-1
% 在一个cell中,由于存在这相同的重复结构,所以这些重复的结构之间首尾相连处也应该存在这hopping
% 这样才能构成一个完整的元胞链
ham(m*4,m*4+1) = t;
ham(m*4+1,m*4) = t;
end
%----------------------------------------
% intra-cell 之间的问题已经考虑完全,现在开始考虑inter-cell之间的hopping
% 既然每一个cell被看作是一个点,那么现在cell与cell之间的hopping则就有位相了
% 相邻的两个cell之间会有两个位置是重叠在一起的,所以标号为1 的原子位置可以hopping到 标号为0的位置上
% 同理2--->3
% 一定要在原来的intre-cell的基础上加上inter-cell的hopping
for m = 0:N-1
ham(m*4+2,m*4+1) = ham(m*4+2,m*4+1)+t*exp(1i*kx);
ham(m*4+1,m*4+2) = ham(m*4+1,m*4+2)+t*exp(-1i*kx);
ham(m*4+3,m*4+4) = ham(m*4+3,m*4+4)+t*exp(-1i*kx);
ham(m*4+4,m*4+3) = ham(m*4+4,m*4+3)+t*exp(1i*kx);
end
end
石墨烯Armchair边界态计算
将上面对Zigzag边界态的分析,旋转90度之后,再对Armchair边界态分析一番,既可以得到Armchair边界态的哈密顿量
clear;clc;
global N len t m0
N = 40;%一个元胞内的重复结构的数目
len = 4*N;
t = 1.0;
m0 = 0;
dlist = 300;
val = zeros(len,dlist);
klist = linspace(-2*pi,2*pi,dlist);
for i = 1:length(klist)
ham = f1(klist(i));
val(:,i) = eig(ham);
end
plot(klist,val)
xlabel('k_y')
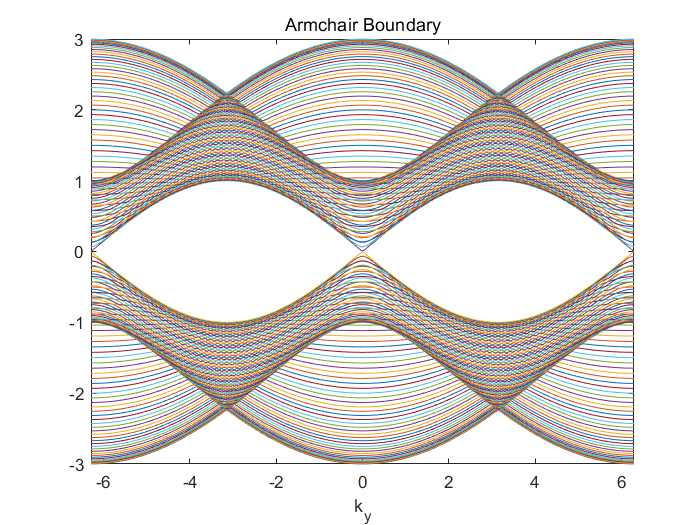
title('Armchair Boundary')
axis([-2*pi 2*pi -3*t 3*t])
%---------------------------------------------------
function ham = f1(kx)
global N t m0 len
ham = zeros(len,len);
for m = 0:N-1
% on-site mass term
ham(m*4+1,m*4+1) = m0;
ham(m*4+2,m*4+2) = -m0;
ham(m*4+3,m*4+3) = m0;
ham(m*4+4,m*4+4) = -m0;
%-- 相同的重复结构中hopping
ham(m*4+1,m*4+2) = t;
ham(m*4+2,m*4+1) = t;
ham(m*4+2,m*4+3) = t;
ham(m*4+3,m*4+2) = t;
ham(m*4+3,m*4+4) = t;
ham(m*4+4,m*4+3) = t;
end
% 相同的重复结构间hopping
% 在一个cell中,由于存在这相同的重复结构,所以这些重复的结构之间首尾相连处也应该存在这hopping
% 这样才能构成一个完整的元胞链
for m = 0:N-2
ham(m*4+2,(m+1)*4+1) = t;
ham((m+1)*4+1,m*4+2) = t;
ham(m*4+3,(m+1)*4+4) = t;
ham((m+1)*4+4,m*4+3) = t;
end
% inter-cell hopping
for m = 0:N-1
ham(m*4+1,m*4+4) = ham(m*4+1,m*4+4) + t*exp(1i*kx);
ham(m*4+4,m*4+1) = ham(m*4+4,m*4+1) + t*exp(-1i*kx);
end
% % extra intra-cell hopping
% ham(4*N-2,4*N+1) = t;
% ham(4*N+1,4*N-2) = t;
%
% ham(4*N-1,len) = t;
% ham(len,4*N-1) = t;
% % extra inter-cell hopping
% ham(4*N+1,len-1) = ham(4*N+1,len-1) + t*exp(1i*kx);
% ham(len-1,4*N+1) = ham(len-1,4*N+1) + t*exp(-1i*kx);
end
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |