超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]
非均匀配对前面考虑的电子配对在实空间以及动量空间中都是均匀的,接下来考虑序参量依赖于空间位置,将均匀$\Delta$推广到缓慢变化的$\Delta(\mathbf{r})$。考虑更一般的时空依赖...
超导自由能泛函(Ginzburg–Landau)推导[空间均匀配对]
超导自由能泛函(Ginzburg–Landau)推导考虑无自旋轨道耦合、无外场、各向同性普通金属的费米气体。动能项写成 H_0=\sum_{\mathbf{k},\sigma}\xi_{\ma...
超导中的Fulde-Ferrell 态与Larkin-Ovchinnikov态
超导中的Fulde-Ferrell 态与Larkin-Ovchinnikov态通常超导态中的库珀对是由动量相反的电子($k, \uparrow$)和($-k, \downarrow$)组成的,总...
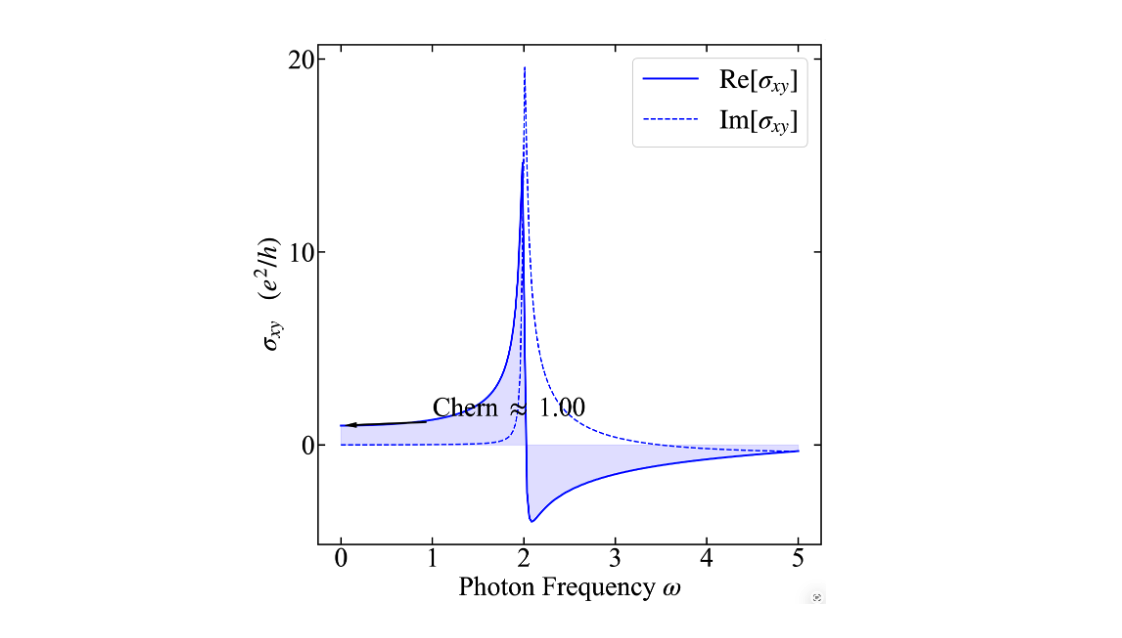
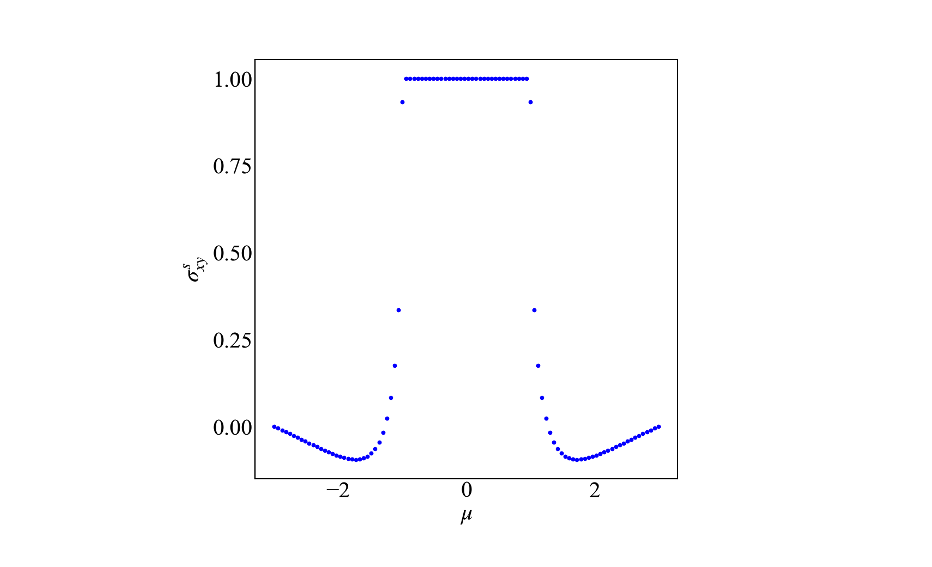
Kwant模拟half-BHZ模型计算Hall电导
简单整理一下用Kwant模拟half-BHZ模型计算Hall电导,帮助理解一下手性边界态。 12345678910111213141516171819202122232425262728293...
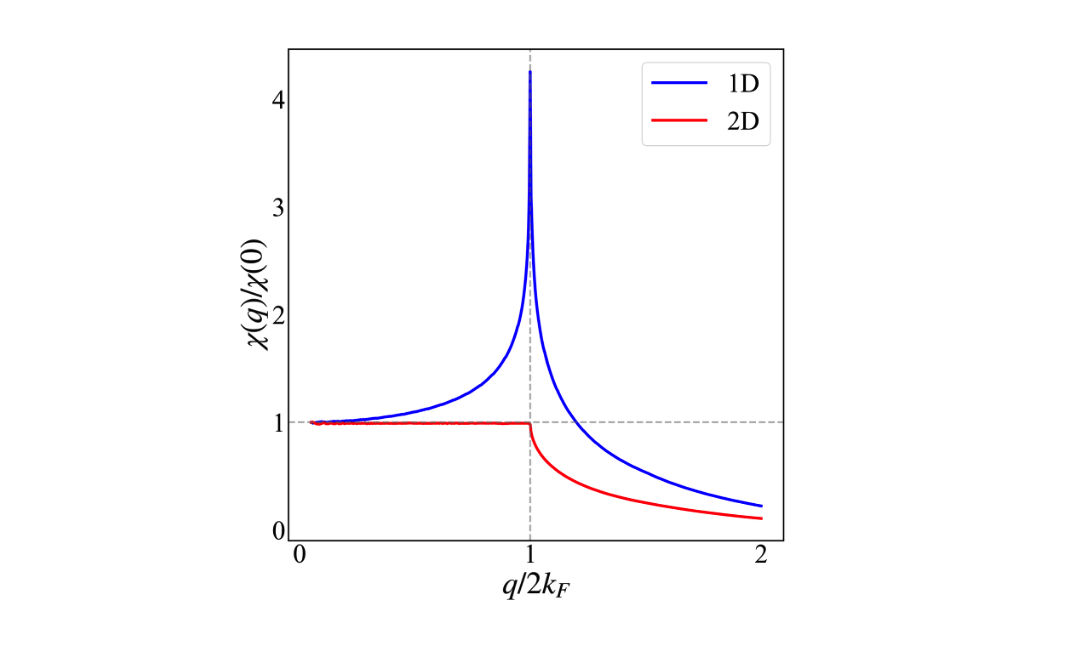
一维与二维体系的静态极化率(数值计算)
极化率计算公式为 \Pi(q) = \frac{1}{N} \sum_{k} \frac{f(\epsilon_k) - f(\epsilon_{k+q})}{\epsilon_k - \ep...
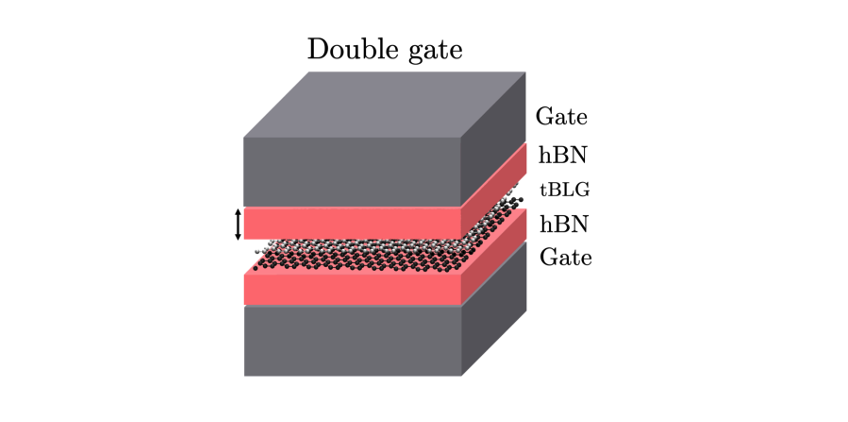
二维体系中的双栅屏蔽库仑势(Dual-gate-screened Coulomb potential)
双栅屏蔽库仑势假设有一个2D电子平面位于 $z=0$。在其上方 $z=d_s$ 和下方 $z=-d_s$ 处,各有一个接地(或电位恒定)的金属平面。电子层所在的介质介电常数为 $\epsilon...
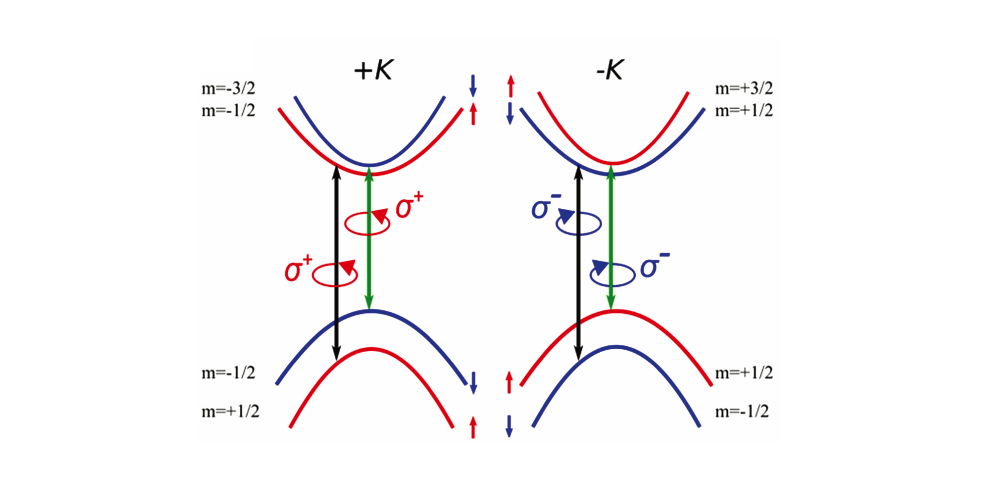
对称性约束光学跃迁
对称性约束光学跃迁在电偶极近似下,光学跃迁振幅由矩阵元决定 M_{if} = \langle \psi_f | \hat{H}' | \psi_i \rangle其中,$\hat{H}’$ 是...
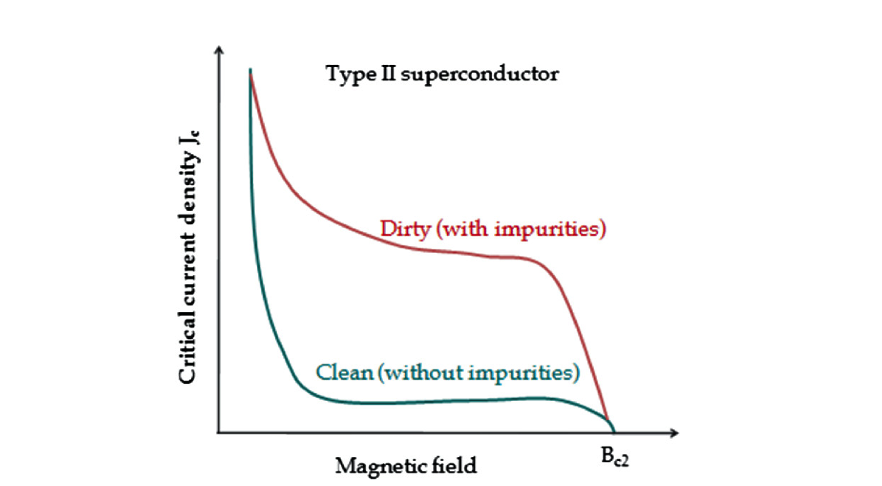
超导中的 Clean limit 与 Dirty limit
超导中的 Clean limit 与 Dirty limit在金属超导中,杂质/缺陷会导致弹性散射,用平均自由程$\ell$(或散射时间$\tau$)来刻画。超导凝聚的一个关键长度尺度是相干长度...


![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)