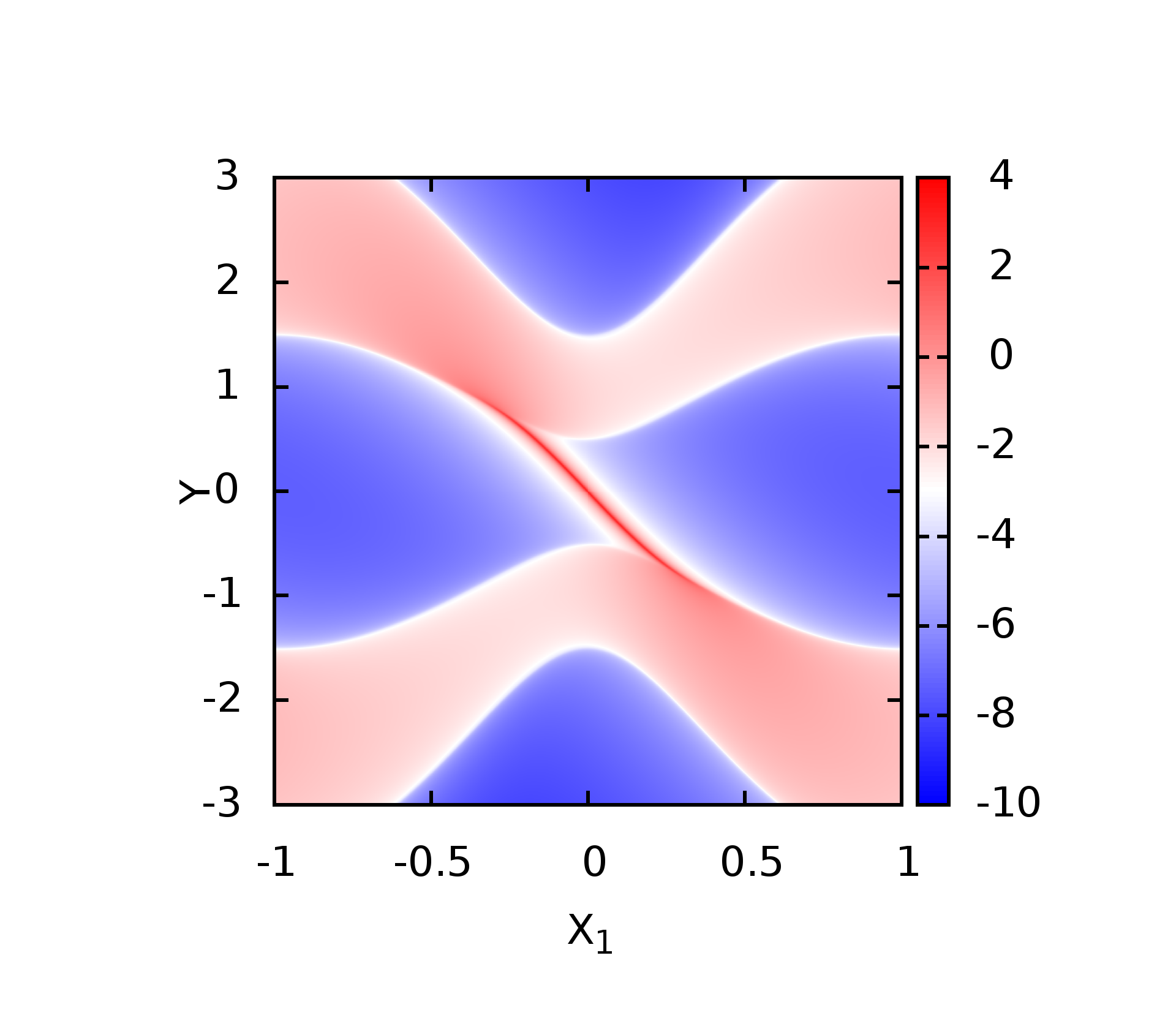
两种方法计算Chern Number
计算Chern数是最初学习拓扑物理都会遇到的问题,正好在假期空闲的时候自己学习了一下Chern数的数值计算方法,在博客上记录一下希望可以帮助到别人。
{:.info}
具体的计算方法和细节就不在这里说明了,只要是想学习计算Chern数的肯定了解它在凝聚态物理中的角色,而计算的细节也会在后面的参考文献中给出,只是展示一下结果。
Julia语言计算Chern number
Version1
这个方法是直接用定义直接计算的结果,但是可能会遇到波函数规范选择的问题,会导致结果有误,而具体的规范问题,我并不懂,所以一般我会选择第二种方法来计算,也就是后面参考文献中介绍的方法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74import Pkg
Pkg.add("LinearAlgebra")
Pkg.add("PyPlot")
using LinearAlgebra,PyPlot
function matSet(kx::Float64,ky::Float64)::Matrix{ComplexF64}
m0::Float64 = -1.0
t1::Float64 = 1.0
t2::Float64 = 1.0
t3::Float64 = 0.5
# 这里选取的是量子反常Hall效应的模型
ham = zeros(ComplexF64,2,2)
ham[1,1] = m0 + 2*t3*sin(kx) + 2*t3*sin(ky) + 2*t2*cos(kx + ky)
ham[2,2] = -(m0 + 2*t3*sin(kx) + 2*t3*sin(ky) + 2*t2*cos(kx + ky))
ham[1,2] = 2*t1*cos(kx) - 1im*2*t1*cos(ky)
ham[2,1] = conj(ham[1,2])
return ham
end
#--------------------------------------------------------------------------
function ux(kx::Float64,ky::Float64,ne::Int64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky))[:,1]
#-----
wx = eigvecs(matSet(kx + del,ky))[:,1]
#------
return w0'*wx/abs(w0'*wx)
end
#---------------------------------------------------------------------------
function uy(kx::Float64,ky::Float64,ne::Int64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky))[:,1]
#-----
wy = eigvecs(matSet(kx,ky + del))[:,1]
#------
return w0'*wy/abs(w0'*wy)
end
#---------------------------------------------------------------------------
function img1(xlist::Array{Float64},ylist::Array{Float64},zlist::Array{ComplexF64})
zlist = map(imag,zlist)
#p1 = scatter(xlist,ylist,zlist*20,c=zlist*0.1,edgecolors="b",cmap="Reds")
p1 = scatter(xlist,ylist,zlist*200,c=zlist,cmap="Reds")
colorbar(p1)
xlabel("kx")
ylabel("ky")
title("Berry Curvature")
savefig("Berry Curature.png",bbox_inches="tight",dpi=60)
end
#----------------------------------------------------------------------------
function main(ne::Int64)
del::Float64 = pi/ne
kx::Float64 = 0.0
ky::Float64 = 0.0
flux::ComplexF64 = 0.0 + 0.0im
chern_num::ComplexF64 = 0.0 + 0.0im
kxlist = Float64[]
kylist = Float64[]
flist = ComplexF64[]
for m1 = -ne:ne
kx = m1*pi/ne
for m2 = -ne:ne
append!(kxlist,kx)
ky = m2*pi/ne
append!(kylist,ky)
flux = log((ux(kx,ky,ne)*uy(kx + del,ky,ne))/(ux(kx,ky + del,ne)*uy(kx,ky,ne)))
append!(flist,flux)
chern_num = chern_num + flux
end
end
img1(kxlist,kylist,flist)
return round(real(chern_num/(2.0*pi*1im)))
end
#--------------------------------------------
main(100)
Version2
1 | using LinearAlgebra,PyPlot |
Python Version
在这里要声明,Python版本的是我从关济寰的网站上复制过来的,必须声明一下版权问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64import numpy as np
import matplotlib.pyplot as plt
from math import * # 引入pi, cos等
import time
def hamiltonian(kx, ky): # 量子反常霍尔QAH模型(该参数对应的陈数为2)
t1 = 1.0
t2 = 1.0
t3 = 0.5
m = -1.0
matrix = np.zeros((2, 2))*(1+0j)
matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
matrix[1, 1] = -matrix[0,0]
return matrix
def main():
start_clock = time.time()
n = 50 # 积分密度
delta = 1e-9 # 求导的偏离量
chern_number = 0 # 陈数初始化
for kx in np.linspace(-pi, pi, n):
for ky in np.linspace(-pi, pi, n):
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 价带波函数([0]即代表取的是填充的能带波函数)
# print(np.argsort(np.real(eigenvalue))[0]) # 排序索引(从小到大)
# print(eigenvalue) # 排序前的本征值
# print(np.sort(np.real(eigenvalue))) # 排序后的本征值(从小到大)
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx的波函数
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离ky的波函数
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx和ky的波函数
# 价带的波函数的贝里联络(berry connection) # 求导后内积
A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta) # 贝里联络Ax(x分量)
A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta) # 贝里联络Ay(y分量)
A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta) # 略偏离ky的贝里联络Ax
A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta) # 略偏离kx的贝里联络Ay
# 贝里曲率(berry curvature)
F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta
# 陈数(chern number)
chern_number = chern_number + F*(2*pi/n)**2
chern_number = chern_number/(2*pi*1j)
print('Chern number = ', chern_number)
end_clock = time.time()
print('CPU执行时间(min)=', (end_clock-start_clock)/60)
if __name__ == '__main__':
main()
Julia调用Python计算Chern 数
1 | # Package import which required |
Julia 并行版
1 | using DelimitedFiles |
参考文献
- Chern Numbers in Discretized Brillouin Zone
- Numerical determination of Chern numbers and critical exponents for Anderson localization in tight-binding and related models
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |