看文献的时候，经常会遇到哈密顿量通常使用Pauli矩阵写出来，然后告诉你基矢的形式，但是每个人的习惯不同就会使的同一个哈密顿量可以有不同形式的写法，恰好这个问题也困扰我很久，所以正好借此将这个基矢的形式问题搞明白。
{:.success}

普通形式

基矢选择为$\Psi_{\mathbf{k}}=\left(c_{a, \mathbf{k} \uparrow}, c_{b, \mathbf{k} \uparrow}, c_{a, \mathbf{k} \downarrow}, c_{b, \mathbf{k} \downarrow}, c_{a,-\mathbf{k} \uparrow}^{\dagger}, c_{b,-\mathbf{k} \uparrow}^{\dagger}, c_{a,-\mathbf{k} \downarrow}^{\dagger}, c_{b,-\mathbf{k} \downarrow}^{\dagger}\right)^{T}$

$
H(\mathbf{k})= M(\mathbf{k}) \sigma_{z} \tau_{z}+A_{x} \sin k_{x} \sigma_{x} s_{z}+A_{y} \sin k_{y} \sigma_{y} \tau_{z}
+\Delta(\mathbf{k}) s_{y} \tau_{y}-\mu \tau_{z}
$

这里$\sigma,s,\tau$代表的是不同自由度的Pauli矩阵(轨道(a,b) 自旋($\uparrow,\downarrow$) 粒子空穴)，它们之间是直积的形式(学物理为了偷懒，一般都直接省略直积符号，所以不熟悉的话就会认为是矩阵相乘了，这一点一定要搞清楚)

这里做直积展开也是有要求的，并不是按照任意的自由度顺序进行的，而是和基矢的表达息息相关，所以这也就是这篇博客的主要目的，完全搞清楚到底基矢选择和Hamiltonian构建如何一一对应

从上面的基矢中可以得到这样的一个信息:轨道(a,b) 是离的最近的，即你所看到的任意相邻的算符都是不同轨道；接下来就是自旋($\uparrow,\downarrow$)，相同的自旋之间相隔有1个算符；最后就是particle-hole形式了，相同轨道相同自旋的粒子算符和空穴算符相隔3个算符，在明确了上面的关系后，那么直积的顺序也就明了了(不明白矩阵直积一定先要看一下，不然这段话你可能在图像上不是很清晰)，直积的顺序是$\tau\otimes s\otimes \sigma$，按照这样的顺序将上面哈密顿量中的每一项写出来，就可以得到正确的形式了。

小技巧

上面所讲的都是一个流程化的东西，只要你看到的哈密顿量是按照上面形式写的，你就可以完全follow上面的内容，把你的哈密顿量写出来。但是也有其它的方法可以让你将上面的哈密顿量正确的写出来。

首先忘记关于基矢的选择，完全不关心基矢到底是怎么样的，从$H({\mathbf{k}})$中你唯一可以得到的是这个哈密顿量有三个内部自由度(轨道$\sigma$，自旋s，粒子空穴$\tau$)。以第一项$M({\mathbf{k}})\sigma_z\tau_z$为例，可以看到它的不同轨道的$M({\mathbf{k}})$是相反的($\sigma_z$一个元素为+1，另一个为-1，且很明显这一项中不同轨道是没有耦合的)，由于这一项中自旋Pauli矩阵为$s_0$ ，所以这一项不同自旋的取值是相同的，即就是这一项自旋简并$s_0$，不同轨道反号$\sigma_z$，粒子部分与空穴部分反号$\tau_z$。 剩余的所有项也是按照这样的逻辑分析，比如$\sigma_x$说明两个轨道是要耦合的，且$C^\dagger_{a}C_{b}=C^\dagger_bC_a$，这里的等号是这两项前面的值相等，请不要误认为是算符相等。

接下来构建矩阵的时候，你的基矢可以根据自己的喜好随意排列比如$\Psi^\dagger=(c^\dagger_{ka\uparrow},c^\dagger_{-ka\uparrow},c^\dagger_{kb\uparrow},c^\dagger_{-kb\uparrow},c_{ka\downarrow},c_{-ka\downarrow},c_{kb\downarrow},c_{-kb\downarrow})$，你只需要在对应的矩阵元位置上，算符组合后的系数满足上面的分析即可，这样的方式得到的结果和上面标准的流程是完全相同的。

上面使用的哈密顿量是来自于下面这篇文献，感兴趣可以试试这两种方案

复杂形式

和简单形式一样，哈密顿量同样是用Pauli矩阵写的，但是这时候基矢里面也会混入Pauli算符，所以如果按照上面标准的流程，哈密顿量就不是那么直接的可以写出来。

此时的基矢为$\hat{C_\mathbf{k}}=(c_\mathbf{k},-i s_{y} c_{-\mathbf{k}}^{\dagger})^T$,$c_\mathbf{k}=(c_{\mathbf{k}a\uparrow},c_{\mathbf{k}b\uparrow},c_{\mathbf{k}a\downarrow},c_{\mathbf{k}b\downarrow})^T$，在这里Pauli矩阵的分析还是和上面一样的，包括直积的顺序，唯一不同的就是这时候基矢中存在Pauli矩阵，不用慌，存在那就将它作用就可以，这里同样采用了简写形式，轨道的$\sigma_0$并没有写出来，故完整的形式应该是$-is_y\sigma_0$，将这个4*4的矩阵作用到基矢上可以得到完整的形式$\hat{C_\mathbf{k}}=(c_{\mathbf{k}a\uparrow},c_{\mathbf{k}b\uparrow},c_{\mathbf{k}a\downarrow},c_{\mathbf{k}b\downarrow},-c^\dagger_{\mathbf{-k}a\downarrow},-c^\dagger_{-\mathbf{k}b\downarrow},c^\dagger_{\mathbf{-k}a\uparrow},c^\dagger_{-\mathbf{k}b\uparrow})$

这时候会发现基矢中出现了负号，展开之后好像又可以用上面简单形式介绍的标准流程了，这是个坑，我已经踩过了。这个时候构建矩阵，你需要把基矢中的负号吸收到矩阵中的元素中去，从而才能保证你进行的是上面的标准流程，否则结果是错了，以这个哈密顿量为例，进行实际操作看看。

方法1

首先可以分析到Pauli矩阵直积的顺序:$\tau\otimes s\otimes\sigma $，这首先将$H({\mathbf{k}})$写成矩阵形式为(我把化学势略去了)

上面这是不考虑基矢中的负号构建的Hamiltonian矩阵，可以尝试去算一下这中形式下的边界态(y方向开边界，x方向是周期的)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
!   https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.227001
!   直接以哈密顿量的形式构建矩阵，并未考虑基矢的形式，结果与文章不符合
!   编译命令为 ifort -mkl file-name.f90
    module pub
    implicit none
    integer xn,N
    parameter(xn = 50,N = xn*8)
    real,parameter::pi = 3.1415926535
    complex,parameter::im = (0.0,1.0)  !虚数单位
    complex::Ham(N,N) = 0
!=================================
    real m0   !Driac mass
    real tx,ty
    real lamx,lamy
    real del0
    real h  ! Zeeman field
    complex::g1(8,8) = 0
    complex::g2(8,8) = 0
    complex::g3(8,8) = 0
    complex::g4(8,8) = 0
    complex::g5(8,8) = 0
!================MKL===============
    integer::lda = N
    integer,parameter::lwmax=2*N+N**2
    real,allocatable::w(:)
    complex,allocatable::work(:)
    real,allocatable::rwork(:)
    integer,allocatable::iwork(:)
    integer lwork   ! at least 2*N+N**2
    integer lrwork    ! at least 1 + 5*N +2*N**2
    integer liwork   ! at least 3 +5*N
    integer info
end module pub
!================= PROGRAM START ============================
    program ex01
    use pub
    integer m,l,i
    real ky
    !=====================
    allocate(w(N))
    allocate(work(lwmax))
    allocate(rwork(1+5*N+2*N**2))
    allocate(iwork(3+5*N))
    !--------------------------
    m0 = 1.0
    tx = 1.0
    ty = 1.0
    lamx = 1.0
    lamy = 1.0
    del0 = 0.4
    h = 0.4
    call band()
    stop 
    end program
!========================================================================
    subroutine band()
    use pub
    real ky,dk
    dk = 0.01*pi
    open(20,file="x-open.dat")
    do ky = -pi,pi,dk
        call openx(ky)
        write(20,999)ky/pi,(w(i),i = 1,N)
    end do
    close(20)
999 format(401f11.6)
    end subroutine band
!======================== Pauli Matrix driect product============================
    subroutine Pauli()
    use pub
!=== Matrix settinf =====
    g1(1,5) = 1 ! del0
    g1(2,6) = 1
    g1(3,7) = 1
    g1(4,8) = 1
    g1(5,1) = 1
    g1(6,2) = 1
    g1(7,3) = 1
    g1(8,4) = 1 
!======
    g2(1,1) = 1  ! kesi0
    g2(2,2) = -1
    g2(3,3) = 1
    g2(4,4) = -1
    g2(5,5) = -1
    g2(6,6) = 1
    g2(7,7) = -1
    g2(8,8) = 1
!======
    g3(1,2) = -im !Lam_y
    g3(2,1) = im
    g3(3,4) = -im
    g3(4,3) = im
    g3(5,6) = im
    g3(6,5) = -im
    g3(7,8) = im
    g3(8,7) = -im
!======
    g4(1,3) = 1 ! h
    g4(2,4) = 1
    g4(3,1) = 1
    g4(4,2) = 1
    g4(5,7) = 1
    g4(6,8) = 1
    g4(7,5) = 1
    g4(8,6) = 1
!============
    g5(1,2) = 1 ! lam_x
    g5(2,1) = 1
    g5(3,4) = -1
    g5(4,3) = -1
    g5(5,6) = -1
    g5(6,5) = -1
    g5(7,8) = 1
    g5(8,7) = 1
    return
    end subroutine Pauli
!==========================================================
    subroutine openx(ky)
    use pub
    real ky
    integer m,l,k
    call Pauli()
    Ham = 0
    !=================== Non-diag Term========================
    do k = 0,xn-1
        if (k == 0) then
            do m = 1,8
                do l = 1,8
                    Ham(m,l) = 2*lamy*sin(ky)*g3(m,l) + (m0 - 2*ty*cos(ky))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(m,l + 8) = -im*lamx*g5(m,l) - tx*g2(m,l)
                end do
            end do
        elseif ( k == xn-1 ) then
            do m = 1,8
                do l = 1,8
                    Ham(k*8 + m,k*8 + l) = 2*lamy*sin(ky)*g3(m,l) + (m0 - 2*ty*cos(ky))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(k*8 + m,k*8 + l-8) = im*lamx*g5(m,l) - tx*g2(m,l)
                end do
            end do
        else
            do m = 1,8
                do l = 1,8
                    Ham(k*8 + m,k*8 + l) = 2*lamy*sin(ky)*g3(m,l) + (m0 - 2*ty*cos(ky))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(k*8 + m,k*8 + l+8) = -im*lamx*g5(m,l) - tx*g2(m,l)
                    Ham(k*8 + m,k*8 + l-8) = im*lamx*g5(m,l) - tx*g2(m,l)
                end do
            end do
        end if
    end do
    call ishermitian()
    call eigsol()
    end subroutine openx
!============================================================
    subroutine ishermitian()
    use pub
    integer i,j
    do i = 1,N
        do j = 1,N
            if (Ham(i,j) .ne. conjg(Ham(j,i)))then
                open(160,file = 'hermitian.dat')
                ccc = ccc +1
                write(160,*)i,j
                write(160,*)Ham(i,j)
                write(160,*)Ham(j,i)
                write(160,*)"===================="
                stop
            end if
        end do
    end do
    close(160)
    return
    end subroutine ishermitian
!================= 矩阵本征值求解 ==============
    subroutine eigSol()
    use pub
    lwork = -1
    liwork = -1
    lrwork = -1
    call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    lwork = min(2*N+N**2, int( work( 1 ) ) )
    lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
    liwork = min(3+5*N, iwork( 1 ) )
    call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    if( info .GT. 0 ) then
        open(110,file="mes.txt",status="unknown")
        write(110,*)'The algorithm failed to compute eigenvalues.'
        close(110)
    end if
    open(120,file="eigval.dat",status="unknown")
    do m = 1,N
        write(120,*)m,w(m)
    end do
    close(120)
    return
    end subroutine eigSol

结果如下

png

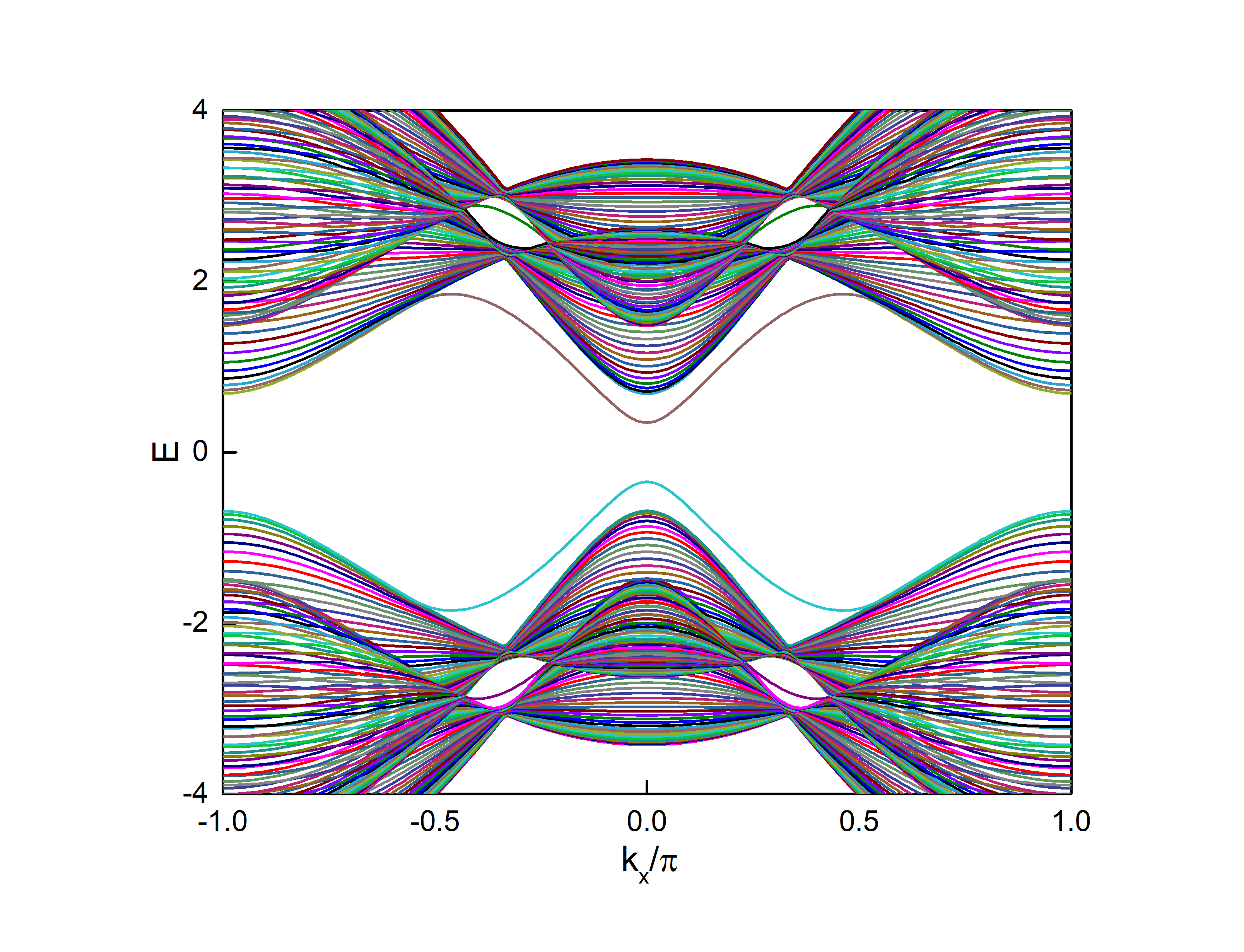
这个结果是错误的，在同样的参数下与文章并不一致，所以记住上面的做法是错误的。

方法2

显然，忽略了基矢中的负号是个错误的选择，那么怎么把这个负号放回去。哈密顿量的矩阵是按照这个的方式构造的，上面按个错误的方法，我们只是简单的算了这里面的$H({\mathbf{k}})$，所以正确的做法是此时看基矢中哪些项的组合会又额外的负号，需要将这个负号吸收进如矩阵中，具体的过程自己算一下矩阵的乘法就完全明白了，这里就不赘述了，直接上结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
!   https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.227001
!   考虑基矢的形式
    module pub
    implicit none
    integer xn,N
    parameter(xn = 50,N = xn*8)
    real,parameter::pi = 3.1415926535
    complex,parameter::im = (0.0,1.0)  !虚数单位
    complex::Ham(N,N)
!=================================
    real tx,ty,lamx,lamy,m0,del0,h
    complex::g1(8,8) = 0
    complex::g2(8,8) = 0
    complex::g3(8,8) = 0
    complex::g4(8,8) = 0
    complex::g5(8,8) = 0
!================MKL===============
    integer::lda = N
    integer,parameter::lwmax=2*N+N**2
    real,allocatable::w(:)
    complex,allocatable::work(:)
    real,allocatable::rwork(:)
    integer,allocatable::iwork(:)
    integer lwork   ! at least 2*N+N**2
    integer lrwork    ! at least 1 + 5*N +2*N**2
    integer liwork   ! at least 3 +5*N
    integer info
end module pub
!================= PROGRAM START ============================
    program ex01
    use pub
    integer m,l,i
    real kx
    !=====================
    allocate(w(N))
    allocate(work(lwmax))
    allocate(rwork(1+5*N+2*N**2))
    allocate(iwork(3+5*N))
    !--------------------------
    m0 = 1.0
    tx = 1.0
    ty = 1.0
    lamx = 1.0
    lamy = 1.0
    del0 = 0.4
    h = 0.4
    call band()
    stop 
    end program
!========================================================================
    subroutine band()
    use pub
    real kx,dk
    dk = 0.01*pi
    open(20,file="y-open.dat")
    do kx = -pi,pi,dk
        call openy(kx)
        write(20,999)kx/pi,(w(i),i = 1,N)
    end do
    close(20)
999 format(401f11.6)
    end subroutine band
!======================== Pauli Matrix driect product============================
    subroutine Pauli()
    use pub
!=== Matrix settinf =====
    g1(1,5) = -1 ! del0
    g1(2,6) = -1
    g1(3,7) = 1
    g1(4,8) = 1
    g1(5,1) = -1
    g1(6,2) = -1
    g1(7,3) = 1
    g1(8,4) = 1 
!======
    g2(1,1) = 1  ! kesi0
    g2(2,2) = -1
    g2(3,3) = 1
    g2(4,4) = -1
    g2(5,5) = -1
    g2(6,6) = 1
    g2(7,7) = -1
    g2(8,8) = 1
!======
    g3(1,2) = -im !Lam_y
    g3(2,1) = im
    g3(3,4) = -im
    g3(4,3) = im
    g3(5,6) = im
    g3(6,5) = -im
    g3(7,8) = im
    g3(8,7) = -im
!======
    g4(1,3) = 1 ! h
    g4(2,4) = 1
    g4(3,1) = 1
    g4(4,2) = 1
    g4(5,7) = -1
    g4(6,8) = -1
    g4(7,5) = -1
    g4(8,6) = -1
!============
    g5(1,2) = 1 ! lam_x
    g5(2,1) = 1
    g5(3,4) = -1
    g5(4,3) = -1
    g5(5,6) = -1
    g5(6,5) = -1
    g5(7,8) = 1
    g5(8,7) = 1
    return
    end subroutine Pauli
!==========================================================
    subroutine openy(kx)
    use pub
    real kx
    integer m,l,k
    call Pauli()
    Ham = 0
    !=================== Non-diag Term========================
    do k = 0,xn-1
        if (k == 0) then
            do m = 1,8
                do l = 1,8
                    Ham(m,l) = 2*lamx*sin(kx)*g5(m,l) + (m0 - 2*tx*cos(kx))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(m,l + 8) = -im*lamy*g3(m,l) - ty*g2(m,l)
                end do
            end do
        elseif ( k == xn-1 ) then
            do m = 1,8
                do l = 1,8
                    Ham(k*8 + m,k*8 + l) = 2*lamx*sin(kx)*g5(m,l) + (m0 - 2*tx*cos(kx))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(k*8 + m,k*8 + l - 8) = im*lamy*g3(m,l) - ty*g2(m,l)
                end do
            end do
        else
            do m = 1,8
                do l = 1,8
                    Ham(k*8 + m,k*8 + l) = 2*lamy*sin(kx)*g5(m,l) + (m0 - 2*tx*cos(kx))*g2(m,l) + del0*g1(m,l) + h*g4(m,l)
                    Ham(k*8 + m,k*8 + l + 8) = -im*lamx*g3(m,l) - ty*g2(m,l)
                    Ham(k*8 + m,k*8 + l - 8) = im*lamx*g3(m,l) - ty*g2(m,l)
                end do
            end do
        end if
    end do
    call ishermitian()
    call eigsol()
    end subroutine openy
!============================================================
    subroutine ishermitian()
    use pub
    integer i,j
    do i = 1,N
        do j = 1,N
            if (Ham(i,j) .ne. conjg(Ham(j,i)))then
                open(160,file = 'hermitian.dat')
                ccc = ccc +1
                write(160,*)i,j
                write(160,*)Ham(i,j)
                write(160,*)Ham(j,i)
                write(160,*)"===================="
                stop
            end if
        end do
    end do
    close(160)
    return
    end subroutine ishermitian
!================= 矩阵本征值求解 ==============
    subroutine eigSol()
    use pub
    lwork = -1
    liwork = -1
    lrwork = -1
    call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    lwork = min(2*N+N**2, int( work( 1 ) ) )
    lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
    liwork = min(3+5*N, iwork( 1 ) )
    call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    if( info .GT. 0 ) then
        open(110,file="mes.txt",status="unknown")
        write(110,*)'The algorithm failed to compute eigenvalues.'
        close(110)
    end if
    open(120,file="eigval.dat",status="unknown")
    do m = 1,N
        write(120,*)m,w(m)
    end do
    close(120)
    return
    end subroutine eigSol

png

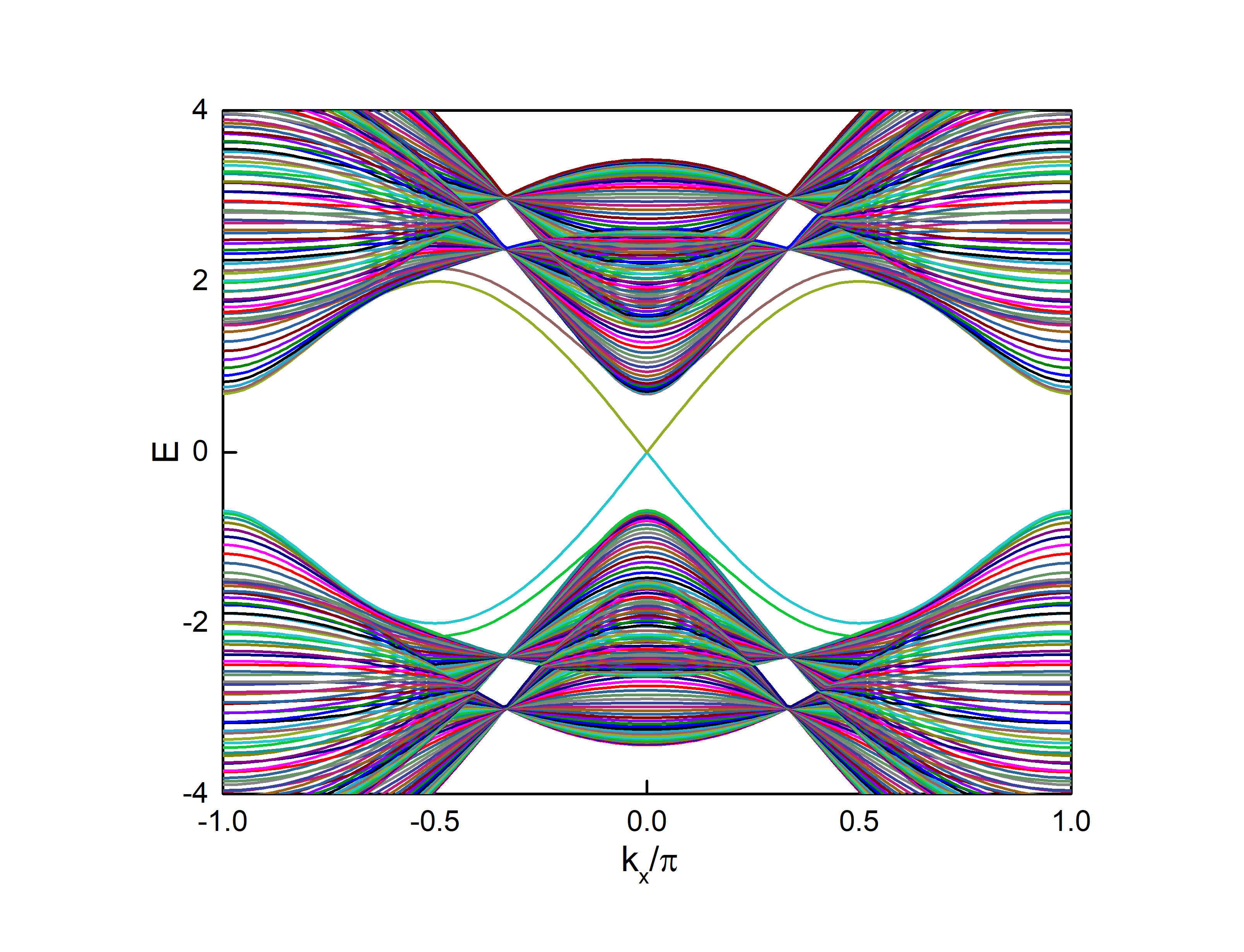
上面的结果和文章中完全符合，这里的内容是参考下面的文章

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
{:.info}

QR Code

Email

yxliphy@gmail.com