平时在做紧束缚模型的时候，都是在n*n的点阵上进行的，但是有时候可能也需要在三角形或者平行四边形样式的点阵上去计算一些性质，正好趁手头空闲就把这个做了一下，还是非常的简单。
{:.info}

正方+三角

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
program e1
implicit none
integer kn
real pi,dk
complex im
parameter(kn = 10,pi = 3.1415926535,im = (0.0,1.0))
integer m1,m2,m3
real t1,t2
complex re1,re2
call cpu_time(t1) ! 获取当前系统时间
open(12,file="squ.dat")
open(13,file="tri.dat")
do m1 = 1,kn
	do m2 = m1,m1+10
		write(12,*)m1,m2,sqrt(1.0*m1+m2)
	end do
end do
!----------------------------
do m1 = 1,kn
	do m2 = 1,m1
		write(13,*)m1,m2,sqrt(1.0*m1+m2)
	end do
end do
close(12)
close(13)
call cpu_time(t2)
stop
end program e1

png{:width=”330px”,:height=”495px”}png{:width=”330px”,:height=”495px”}

六边形区域

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! Graphene BZ plot
    module pub
    implicit none
    complex,parameter::im = (0.0,1.0) 
    real,parameter::pi = 3.14159265359
    integer n0  ! n0 边形
    real r0     ! 外接圆半径
    end module pub
!========== PROGRAM START ==========================
    program sol
    use pub
    call BZ()
    stop
    end program sol
!===================================================
    subroutine BZ()
    use pub
    real dx,dy,d0
    d0 = 0.01
    open(20,file="graphene-BZ.dat")
    do dx = -1.0,-0.5,d0
        do dy = -sqrt(3.0)*dx - sqrt(3.0),sqrt(3.0)*dx + sqrt(3.0),d0
            write(20,*)dx,dy,cos(sin(dx*dy))
        end do
    end do
    do dx = -0.5,0.5,d0
        do dy = -sqrt(3.0)/2.0,sqrt(3.0)/2,d0
            write(20,*)dx,dy,cos(sin(dx*dy))
        end do
    end do
    do dx = 0.5,1.0,d0
        do dy = sqrt(3.0)*dx - sqrt(3.0),-sqrt(3.0)*dx + sqrt(3.0),d0
            write(20,*)dx,dy,cos(sin(dx*dy))
        end do
    end do
    return  
    end subroutine BZ

绘图程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
set encoding iso_8859_1
#set terminal  postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced  font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1920
set output 'density.png'
set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
#set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
#set size ratio -1
set size 1,1 # 图片比列
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-1:1]
set yrange [-1:1]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'hex.dat' u 1:2:3 w pm3d
#splot 'sq45.dat' u 1:2:3 w pm3d

png

正方旋转$45^o$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! Graphene BZ plot
    module pub
    implicit none
    complex,parameter::im = (0.0,1.0) 
    real,parameter::pi = 3.14159265359
    end module pub
!========== PROGRAM START ==========================
    program sol
    use pub
    call sq45()
    stop
    end program sol
!============================================================================
    subroutine sq45()
    use pub
    real dx,dy,d0,ang,k0,b0
    real nx
    nx = 10.0
    ang = pi/4.0
    d0 = 0.1
    k0 = 2*sin(ang)  ! 斜率
    b0 = k0*nx    ! 截距
    
    open(22,file="sq45.dat")
    do dx = -nx,0.0,d0
        do dy = -(k0*dx + b0),k0*dx + b0,d0
            write(22,*)dx,dy,cos(dx*dy)
        end do
        write(22,*)""
    end do
    do dx = 0.0,nx,d0
        do dy = -(-k0*dx + b0),-k0*dx + b0,d0
            write(22,*)dx,dy,cos(dx*dy)
        end do
        write(22,*)""
    end do
    close(22)
    return
    end subroutine sq45

因为撒点太密的话,数据文件会会比较大,此时推荐使用gnuplot绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
set encoding iso_8859_1
#set terminal  postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced  font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1920
set output 'density.png'
set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
#set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
#set size ratio -1
set size 1,1 # 图片比列
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-10:10]
set yrange [-15:15]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'sq45.dat' u 1:2:3 w pm3d

png

三角形点阵哈密顿量

最近遇到要在一个三角形点阵上计算一些内容,需要构建哈密顿量,主要的想法就是将三角形点阵上的index搞清楚,然后构建对应格点上哈密顿量,代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! H(k)=(m0 + tx cos kx + ty cos ky) + ax sin kx + ay sin ky
    module pub
    implicit none
    integer xn,yn,N,len2
    parameter(xn = 30,yn = 30,N = yn*(yn + 1)/2*8,len2 = yn*(yn + 1)/2)
    complex,parameter::im = (0.0,1.0) 
    real,parameter::pi = 3.14159265359
    complex Ham(N,N) 
    integer bry(4,len2)
    real m0,mu,omega,tx,ty,del0,delx,dely,ax,ay,h0  
!-------------------lapack parameter----------------------------------------
    integer::lda = N
    integer,parameter::lwmax = 2*N + N**2
    real,allocatable::w(:)
    complex*8,allocatable::work(:)
    real,allocatable::rwork(:)
    integer,allocatable::iwork(:)
    integer lwork   
    integer lrwork    
    integer liwork   
    integer info
    end module pub
!========== PROGRAM START ==========================
    program sol
    use pub
    !================ Physics memory allocate =================
    allocate(w(N))
    allocate(work(lwmax))
    allocate(rwork(1 + 5*N + 2*N**2))
    allocate(iwork(3 + 5*N))
    !--------------------
    m0 = 1.5   
    tx = 1.0  
    ty = -1.0 
    mu = 0 
    ax = 1.0 
    ay = 1.0
    omega = 0   ! LDOS
    !------------- D(k) = D0 + D_x cos(k_x) + D_y cos(k_y) -
    del0 = 0
    delx = 0.2
    dely = -delx
    call cut()
    ! call matset()
    call ldos(0.0)
    
    stop
    end program sol
!===========================================================
    subroutine boundary2()
    use pub
    integer i,ix,iy
    bry = 0
    do iy = 1,yn  
        do ix = 1,iy 
            i = iy*(iy - 1)/2 + ix
            bry(1,i) = i + 1    ! right hopping
            if(ix.eq.iy)bry(1,i) = bry(1,i) - iy     
            bry(2,i) = i - 1    ! left hopping
            if(ix.eq.1)bry(2,i) = bry(2,i) + iy      
            bry(3,i) = i + iy   ! up hopping
            if(iy.eq.yn)bry(3,i) = (ix + 1)*ix/2
            bry(4,i)= i - (iy - 1)    ! down hopping
            if(iy.eq.ix)bry(4,i) = yn*(yn - 1)/2 + ix
        enddo
    enddo
    open(10,file="index.dat")
    do iy = 1,yn
        do ix = 1,iy
            i = iy*(iy - 1)/2 + ix
            write(10,999)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
        end do
    end do
    close(10)
999format(7I8)
    return
    end subroutine boundary2
!==========================================================
    subroutine cut()
    use pub
    integer ix,iy
    call boundary2()
    do iy = 1,yn  
        do ix = 1,iy 
            i = iy*(iy - 1)/2 + ix
            Ham(i , i) = m0 - mu
            Ham(len2 + i , len2 + i) = -m0 - mu 
            Ham(len2*2 + i , len2*2 + i) = -m0 - mu 
            Ham(len2*3 + i , len2*3 + i) = m0 - mu 
            Ham(len2*4 + i , len2*4 + i) = -m0 + mu  
            Ham(len2*5 + i , len2*5 + i) = m0 + mu 
            Ham(len2*6 + i , len2*6 + i) = m0 + mu 
            Ham(len2*7 + i , len2*7 + i) = -m0 + mu  
            !----------------------------------------------------------
            !(1,1)
            if (ix.ne.iy)Ham(i,bry(1,i)) = tx/2.0
            if (ix.ne.1)Ham(i,bry(2,i)) = tx/2.0
            if (iy.ne.yn)Ham(i,bry(3,i)) = ty/2.0
            if (iy.ne.ix)Ham(i,bry(4,i)) = ty/2.0 


            ! if(ix.ne.iy)write(11,*)iy,ix,i,bry(1,i)
            ! if(ix.ne.1)write(12,*)iy,ix,i,bry(2,i)
            ! if(iy.ne.yn)write(13,*)iy,ix,i,bry(3,i)
            ! if(iy.ne.1)write(14,*)iy,ix,i,bry(4,i)
            !(2,2)
            if (ix.ne.iy)Ham(len2 + i, len2 + bry(1,i)) = -tx/2.0
            if (ix.ne.1)Ham(len2 + i, len2 + bry(2,i)) = -tx/2.0
            if (iy.ne.yn)Ham(len2 + i, len2 + bry(3,i)) = -ty/2.0
            if (iy.ne.ix)Ham(len2 + i, len2 + bry(4,i)) = -ty/2.0
            !(3,3)
            if (ix.ne.iy)Ham(len2*2 + i, len2*2 + bry(1,i)) = -tx/2.0
            if (ix.ne.1)Ham(len2*2 + i, len2*2 + bry(2,i)) = -tx/2.0
            if (iy.ne.yn)Ham(len2*2 + i, len2*2 + bry(3,i)) = -ty/2.0
            if (iy.ne.ix)Ham(len2*2 + i, len2*2 + bry(4,i)) = -ty/2.0
            !(4,4)
            if (ix.ne.iy)Ham(len2*3 + i, len2*3 + bry(1,i)) = tx/2.0
            if (ix.ne.1)Ham(len2*3 + i, len2*3 + bry(2,i)) = tx/2.0
            if (iy.ne.yn)Ham(len2*3 + i, len2*3 + bry(3,i)) = ty/2.0
            if (iy.ne.ix)Ham(len2*3 + i, len2*3 + bry(4,i)) = ty/2.0
            !(5,5)
            if (ix.ne.iy)Ham(len2*4 + i, len2*4 + bry(1,i)) = -tx/2.0
            if (ix.ne.1)Ham(len2*4 + i, len2*4 + bry(2,i)) = -tx/2.0
            if (iy.ne.yn)Ham(len2*4 + i, len2*4 + bry(3,i)) = -ty/2.0
            if (iy.ne.ix)Ham(len2*4 + i, len2*4 + bry(4,i)) = -ty/2.0
            !(6,6)
            if (ix.ne.iy)Ham(len2*5 + i, len2*5 + bry(1,i)) = tx/2.0
            if (ix.ne.1)Ham(len2*5 + i, len2*5 + bry(2,i)) = tx/2.0
            if (iy.ne.yn)Ham(len2*5 + i, len2*5 + bry(3,i)) = ty/2.0
            if (iy.ne.ix)Ham(len2*5 + i, len2*5 + bry(4,i)) = ty/2.0
            !(7,7)
            if (ix.ne.iy)Ham(len2*6 + i, len2*6 + bry(1,i)) = tx/2.0
            if (ix.ne.1)Ham(len2*6 + i, len2*6 + bry(2,i)) = tx/2.0
            if (iy.ne.yn)Ham(len2*6 + i, len2*6 + bry(3,i)) = ty/2.0
            if (iy.ne.ix)Ham(len2*6 + i, len2*6 + bry(4,i)) = ty/2.0
            !(8,8)
            if (ix.ne.iy)Ham(len2*7 + i, len2*7 + bry(1,i)) = -tx/2.0
            if (ix.ne.1)Ham(len2*7 + i, len2*7 + bry(2,i)) = -tx/2.0
            if (iy.ne.yn)Ham(len2*7 + i, len2*7 + bry(3,i)) = -ty/2.0
            if (iy.ne.ix)Ham(len2*7 + i, len2*7 + bry(4,i)) = -ty/2.0
            !=========================================================
            !(1,2)
            if (ix.ne.iy)Ham(i, len2 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(i, len2 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(i, len2 + bry(3,i)) = -im*ay/(2.0*im)
            if (iy.ne.ix)Ham(i, len2 + bry(4,i)) = im*ay/(2.0*im)
            !(2,1)
            if (ix.ne.iy)Ham(len2 + i,bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2 + i,bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2 + i,bry(3,i)) = im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2 + i,bry(4,i)) = -im*ay/(2.0*im)
            !(3,4)
            if (ix.ne.iy)Ham(len2*2 + i, len2*3 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*2 + i, len2*3 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*2 + i, len2*3 + bry(3,i)) = -im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*2 + i, len2*3 + bry(4,i)) = im*ay/(2.0*im)
            !(4,3)
            if (ix.ne.iy)Ham(len2*3 + i, len2*2 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*3 + i, len2*2 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*3 + i, len2*2 + bry(3,i)) = im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*3 + i, len2*2 + bry(4,i)) = -im*ay/(2.0*im)
            !(5,6)
            if (ix.ne.iy)Ham(len2*4 + i, len2*5 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*4 + i, len2*5 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*4 + i, len2*5 + bry(3,i)) = im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*4 + i, len2*5 + bry(4,i)) = -im*ay/(2.0*im)
            !(6,5)
            if (ix.ne.iy)Ham(len2*5 + i, len2*4 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*5 + i, len2*4 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*5 + i, len2*4 + bry(3,i)) = -im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*5 + i, len2*4 + bry(4,i)) = im*ay/(2.0*im)
            !(7.8)
            if (ix.ne.iy)Ham(len2*6 + i, len2*7 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*6 + i, len2*7 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*6 + i, len2*7 + bry(3,i)) = im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*6 + i, len2*7 + bry(4,i)) = -im*ay/(2.0*im)
            !(8,7)
            if (ix.ne.iy)Ham(len2*7 + i, len2*6 + bry(1,i)) = ax/(2.0*im)
            if (ix.ne.1)Ham(len2*7 + i, len2*6 + bry(2,i)) = -ax/(2.0*im)
            if (iy.ne.yn)Ham(len2*7 + i, len2*6 + bry(3,i)) = -im*ay/(2.0*im)
            if (iy.ne.ix)Ham(len2*7 + i, len2*6 + bry(4,i)) = im*ay/(2.0*im)
            !============================================
            !(1,7)
            Ham(i, len2*6 + i) = -del0
            if (ix.ne.iy)Ham(i, len2*6 + bry(1,i)) = -delx
            if (ix.ne.1)Ham(i, len2*6 + bry(2,i)) = -delx
            if (iy.ne.yn)Ham(i, len2*6 + bry(3,i)) = -dely
            if (iy.ne.ix)Ham(i, len2*6 + bry(4,i)) = -dely
            !(2,8)
            Ham(len2 + i, len2*7 + i) = -del0
            if (ix.ne.iy)Ham(len2 + i, len2*7 + bry(1,i)) = -delx
            if (ix.ne.1)Ham(len2 + i, len2*7 + bry(2,i)) = -delx
            if (iy.ne.yn)Ham(len2 + i, len2*7 + bry(3,i)) = -dely
            if (iy.ne.ix)Ham(len2 + i, len2*7 + bry(4,i)) = -dely
            !(3,5)
            Ham(len2*2 + i, len2*4 + i) = del0
            if (ix.ne.iy)Ham(len2*2 + i, len2*4 + bry(1,i)) = delx
            if (ix.ne.1)Ham(len2*2 + i, len2*4 + bry(2,i)) = delx
            if (iy.ne.yn)Ham(len2*2 + i, len2*4 + bry(3,i)) = dely
            if (iy.ne.ix)Ham(len2*2 + i, len2*4 + bry(4,i)) = dely
            !(4,6)
            Ham(len2*3 + i, len2*5 + i) = del0
            if (ix.ne.iy)Ham(len2*3 + i, len2*5 + bry(1,i)) = delx
            if (ix.ne.1)Ham(len2*3 + i, len2*5 + bry(2,i)) = delx
            if (iy.ne.yn)Ham(len2*3 + i, len2*5 + bry(3,i)) = dely
            if (iy.ne.ix)Ham(len2*3 + i, len2*5 + bry(4,i)) = dely
            !(7,1)
            Ham(len2*6 + i,i) = -del0 
            if (ix.ne.iy)Ham(len2*6 + i,bry(1,i)) = -delx
            if (ix.ne.1)Ham(len2*6 + i,bry(2,i)) = -delx
            if (iy.ne.yn)Ham(len2*6 + i,bry(3,i)) = -dely
            if (iy.ne.ix)Ham(len2*6 + i,bry(4,i)) = -dely
            !(8,2)
            Ham(len2*7 + i,len2 + i) = -del0
            if (ix.ne.iy)Ham(len2*7 + i, len2 + bry(1,i)) = -delx
            if (ix.ne.1)Ham(len2*7 + i, len2 + bry(2,i)) = -delx
            if (iy.ne.yn)Ham(len2*7 + i, len2 + bry(3,i)) = -dely
            if (iy.ne.ix)Ham(len2*7 + i, len2 + bry(4,i)) = -dely
            !(5,3)
            Ham(len2*4 + i,len2*2 + i) = del0
            if (ix.ne.iy)Ham(len2*4 + i, len2*2 + bry(1,i)) = delx
            if (ix.ne.1)Ham(len2*4 + i, len2*2 + bry(2,i)) = delx
            if (iy.ne.yn)Ham(len2*4 + i, len2*2 + bry(3,i)) = dely
            if (iy.ne.ix)Ham(len2*4 + i, len2*2 + bry(4,i)) = dely
            !(6,4)
            Ham(len2*5 + i,len*3 + i) = del0
            if (ix.ne.iy)Ham(len2*5 + i, len2*3 + bry(1,i)) = delx
            if (ix.ne.1)Ham(len2*5 + i, len2*3 + bry(2,i)) = delx
            if (iy.ne.yn)Ham(len2*5 + i, len2*3 + bry(3,i)) = dely
            if (iy.ne.ix)Ham(len2*5 + i, len2*3 + bry(4,i)) = dely
        end do
    end do
    !--------------------------------------
    call isHermitian()
    call eigsol()
    return
    end subroutine
!===========================Local Density of State=============================
    subroutine ldos(omg)
    use pub
    integer m,l1,k,l2
    real s,omg
    real,external::delta
    open(12,file="ldos.dat") 
    do l1 = 1,yn
        do l2 = 1,l1
            k = l1*(l1 - 1)/2 + l2
            s = 0
            do m=1,N
                s = s + delta(w(m) - omg)*(abs(Ham(k , m))**2 + abs(Ham(k + len2 , m))**2)&
                + delta(w(m) - omg)*(abs(Ham(k + len2*6 , m))**2 + abs(Ham(k + len2*7 , m))**2)
            end do
            write(12,*)l1,l2,s
        end do
    end do
    close(12)
    return
    end subroutine ldos
!======================================================================
    real function delta(x)
    real x
    real::gamma = 0.001
    delta = 1.0/3.1415926535*gamma/(x*x + gamma*gamma)
    end function delta
!============================================================
    subroutine isHermitian()
    use pub
    integer i,j
    do i = 1,N
        do j = 1,N
            if (Ham(i,j) .ne. conjg(Ham(j,i)))then
                open(160,file = 'hermitian.dat')
                write(160,*)i,j
                write(160,*)Ham(i,j)
                write(160,*)Ham(j,i)
                write(*,*)"Hamiltonian is not Hermitian"
                stop      
            end if
        end do
    end do
    close(160)
    return
    end subroutine isHermitian
!================= Hermitain Matrices solve ==============
    subroutine eigsol(input)
    use pub
    integer m
    lwork = -1
    liwork = -1
    lrwork = -1
    call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    lwork = min(2*N+N**2, int( work( 1 ) ) )
    lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
    liwork = min(3+5*N, iwork( 1 ) )
    call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
    if( info .GT. 0 ) then
        open(110,file="mes.dat",status="unknown")
        write(110,*)'The algorithm failed to compute eigenvalues.'
        close(110)
    end if
    open(120,file = "eigval.dat") 
    do m = 1,N
        write(120,*)m,w(m)
    end do
    close(120)
    return
    end subroutine eigsol

这里重要的部分就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
subroutine boundary2()
use pub
integer i,ix,iy
bry = 0
do iy = 1,yn  
    do ix = 1,iy 
        i = iy*(iy - 1)/2 + ix
        bry(1,i) = i + 1    ! right hopping
        if(ix.eq.iy)bry(1,i) = bry(1,i) - iy     
        bry(2,i) = i - 1    ! left hopping
        if(ix.eq.1)bry(2,i) = bry(2,i) + iy      
        bry(3,i) = i + iy   ! up hopping
        if(iy.eq.yn)bry(3,i) = (ix + 1)*ix/2
        bry(4,i)= i - (iy - 1)    ! down hopping
        if(iy.eq.ix)bry(4,i) = yn*(yn - 1)/2 + ix
    enddo
enddo
open(10,file="index.dat")
do iy = 1,yn
    do ix = 1,iy
        i = iy*(iy - 1)/2 + ix
        write(10,999)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
    end do
end do
close(10)
999format(7I8)
return
end subroutine boundary2

这里就构建了一个下三角点阵,而且使用了周期边界条件.

png

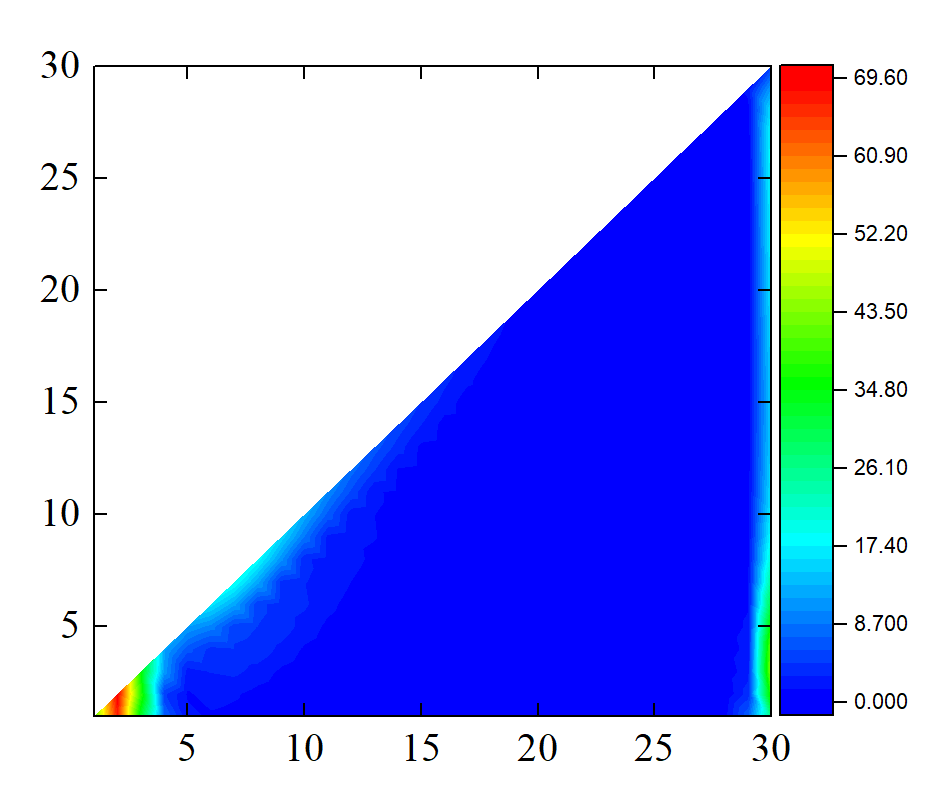
矩形点阵哈密顿量格点

这里尝试构建开边界条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
    module pub
    implicit none
    integer yn,xn,yn1,len2,N
    real pi
    complex im 
    parameter(yn = 10,yn1 = 10,len2 = yn*yn,N = len2 + 2*yn*(yn + 1)/2,pi=3.1415926535,im = (0.0,1.0))
    integer bry(4,len2 + 2*yn*(yn + 1)/2)
    real tx,ty,ax,ay
    complex Ham(N,N)
    end module pub
!=================================================
    program sol
    use pub
    tx = 1.0
    ty = 1.0
    ax = 1.0
    ay = 1.0
    write(*,*)N
    write(*,*)tx,ty,ax,ay,im
    call matset()
    end program sol
!===================================================
    subroutine lattice()
    ! 开边界条件
    use pub
    integer ix,iy,i
    i = 0
    ! ! 下三角
    do iy = 1,yn1  
        do ix = 1,iy 
            ! i = iy*(iy - 1)/2 + ix
            i = i + 1
            bry(1,i) = i + 1    ! right hopping
            if(ix.eq.iy)bry(1,i) = 0  
            bry(2,i) = i - 1    ! left hopping
            if(ix.eq.1)bry(2,i) = 0
            bry(3,i) = i + iy   ! up hopping
            if(iy.eq.yn1)bry(3,i) = 0
            bry(4,i)= i - (iy - 1)    ! down hopping
            if(iy.eq.ix)bry(4,i) = 0
        enddo
    enddo
    ! ! 矩形
    do iy = 1,yn
        do ix = 1,yn
            ! i = yn1*(yn1 + 1)/2 + (iy - 1)*yn + ix
            i = i + 1 
            bry(1,i) = i + 1    !right hopping
            if(ix.eq.xn)bry(1,i) = 0
            bry(2,i) = i - 1    !left hopping
            if(ix.eq.xn)bry(2,i) = 0
            bry(3,i) = i + yn   !up hopping
            if(iy.eq.yn)bry(3,i) = 0
            bry(4,i) = i - yn   !down hopping
            if(iy.eq.1)bry(4,i) = 0
        end do
    end do
    ! ! 上三角
    ! i = yn1*(yn1 + 1)/2 + yn*yn
    ! i = 0
    do iy = 1,yn
        do ix = 1,yn - (iy - 1)
            i = i + 1
            bry(1,i) = i + 1  ! right hopping
            if(ix.eq.yn - (iy - 1))bry(1,i) = 0
            bry(2,i) = i - 1  ! left hopping
            if(ix.eq.1)bry(2,i) = 0
            bry(3,i) = i + yn - iy  ! up hopping
            if(iy.eq.ix)bry(3,i) = 0
            bry(4,i) = i - (yn - iy) ! down hopping
            if(iy.eq.1)bry(4,i) = 0 
        end do
    end do
    open(10,file="pall.dat")
    do i = 1,N
        write(10,888)i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
    end do
    close(10)
888 format(8I8)
    return  
    end subroutine lattice
!=========================================================================
    subroutine matset()
    use pub
    integer i
    call lattice()
    do i = 1,N
        if(bry(1,i).ne.0)ham(i,bry(1,i)) = ax/(2.0*im)
        if(bry(2,i).ne.0)ham(i,bry(2,i)) = -ax/(2.0*im)
        if(bry(3,i).ne.0)ham(i,bry(3,i)) = im*ay/(2.0*im)
        if(bry(4,i).ne.0)ham(i,bry(4,i)) = -im*ay/(2.0*im)
    end do
    !-------------------------------------
    call isHermitian()
    return
    end subroutine 
!============================================================
    subroutine isHermitian()
    use pub
    integer i,j
    do i = 1,N
        do j = 1,N
            if (Ham(i,j) .ne. conjg(Ham(j,i)))then
                open(160,file = 'hermitian.dat')
                write(160,*)i,j
                write(160,*)Ham(i,j)
                write(160,*)Ham(j,i)
                write(*,*)"Hamiltonian is not Hermitian"
                stop      
            end if
        end do
    end do
    close(160)
    return
    end subroutine isHermitian

这里想再利用同样的方式构造矩形点阵的哈密顿量,先进行了简单的尝试(尝试周期性边界条件),暂时未完成.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
module pub
implicit none
integer yn,xn,yn1,len2
parameter(yn = 10,yn1 = 10,len2 = yn*yn)
integer bry(4,len2 + 2*yn*(yn + 1)/2)
end module pub
!=================================================
    program sol
    use pub
    call lattice()
    end program sol
!===================================================
    subroutine lattice()
    use pub
    integer ix,iy,i
    ! ! 下三角
    ! do iy = 1,yn1  
    !     do ix = 1,iy 
    !         i = iy*(iy - 1)/2 + ix
    !         bry(1,i) = i + 1    ! right hopping
    !         if(ix.eq.iy)bry(1,i) = bry(1,i) - iy     
    !         bry(2,i) = i - 1    ! left hopping
    !         if(ix.eq.1)bry(2,i) = bry(2,i) + iy      
    !         bry(3,i) = i + iy   ! up hopping
    !         if(iy.eq.yn1)bry(3,i) = (ix + 1)*ix/2
    !         bry(4,i)= i - (iy - 1)    ! down hopping
    !         if(iy.eq.ix)bry(4,i) = yn1*(yn1 - 1)/2 + ix
    !     enddo
    ! enddo
    ! ! 矩形
    ! do iy = 1,yn
    !     do ix = 1,yn
    !         i = yn1*(yn1 + 1)/2 + (iy - 1)*yn + ix
    !         bry(1,i) = i + 1    !right hopping
    !         if(ix.eq.xn)bry(1,i) = bry(1,i) - xn
    !         bry(2,i) = i - 1    !left hopping
    !         if(ix.eq.xn)bry(2,i) = bry(2,i) + xn
    !         bry(3,i) = i + yn   !up hopping
    !         if(iy.eq.yn)bry(3,i) = bry(3,i) - len2
    !         bry(4,i) = i - yn   !down hopping
    !         if(iy.eq.1)bry(4,i) = bry(4,i) + len2
    !     end do
    ! end do
    ! ! 上三角
    ! i = yn1*(yn1 + 1)/2 + yn*yn
    
    do iy = 1,yn
        do ix = 1,yn - (iy - 1)
            i = i + 1
            bry(1,i) = i + 1  ! right hopping
            if(ix.eq.yn - iy - 1)bry(1,i) = bry(1,i) - (yn - iy) + 1
            bry(2,i) = i - 1  ! left hopping
            if(ix.eq.1)bry(2,i) = bry(2,i) + (yn - iy) + 1
            bry(3,i) = i + yn - iy  ! up hopping
            if(iy.eq.ix)bry(3,i) = bry(3,i) - (yn - iy) + (ix-iy)*(yn - iy)
            bry(4,i) = i - (yn - iy) ! down hopping
            if(iy.eq.1)bry(4,i) = i + yn*(yn + 1)/2 - (yn - iy - 1)*(yn - iy + 1 + 1)/2 + 1 
        end do
    end do
    open(10,file="up_triangle.dat")
    i = 0
    do iy = 1,yn
        do ix = 1,yn - (iy - 1)
            i = i + 1
            write(10,888)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
        end do
    end do
    close(10)
888 format(8I8)
    return  
    end subroutine lattice

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
{:.info}

QR Code

Email

yxliphy@gmail.com