平时在做紧束缚模型的时候,都是在n*n的点阵上进行的,但是有时候可能也需要在三角形或者平行四边形样式的点阵上去计算一些性质,正好趁手头空闲就把这个做了一下,还是非常的简单。
正方+三角
program e1
implicit none
integer kn
real pi,dk
complex im
parameter(kn = 10,pi = 3.1415926535,im = (0.0,1.0))
integer m1,m2,m3
real t1,t2
complex re1,re2
call cpu_time(t1) ! 获取当前系统时间
open(12,file="squ.dat")
open(13,file="tri.dat")
do m1 = 1,kn
do m2 = m1,m1+10
write(12,*)m1,m2,sqrt(1.0*m1+m2)
end do
end do
!----------------------------
do m1 = 1,kn
do m2 = 1,m1
write(13,*)m1,m2,sqrt(1.0*m1+m2)
end do
end do
close(12)
close(13)
call cpu_time(t2)
stop
end program e1
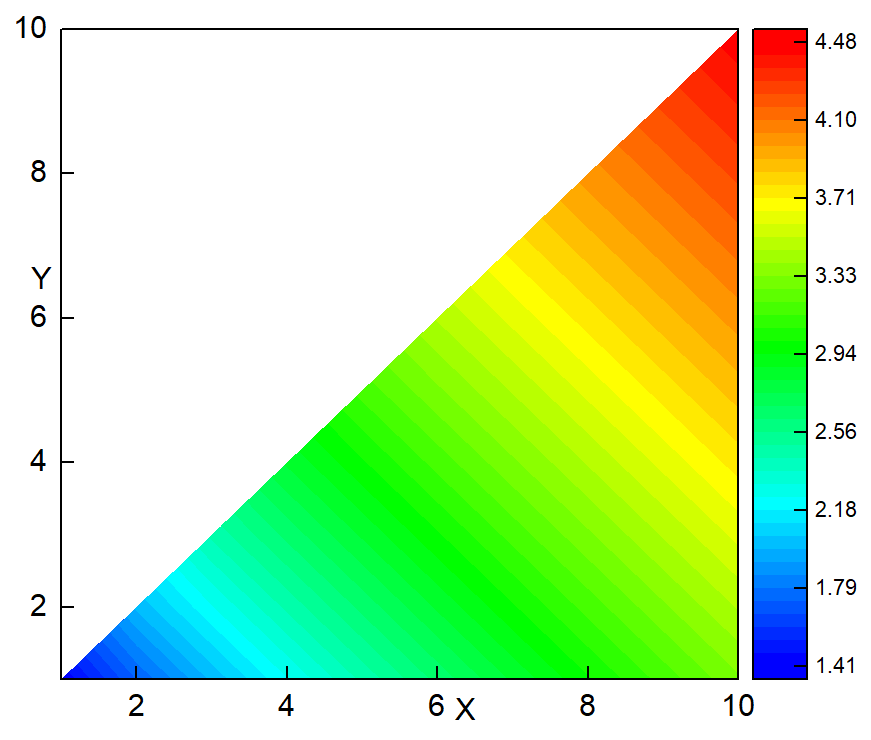
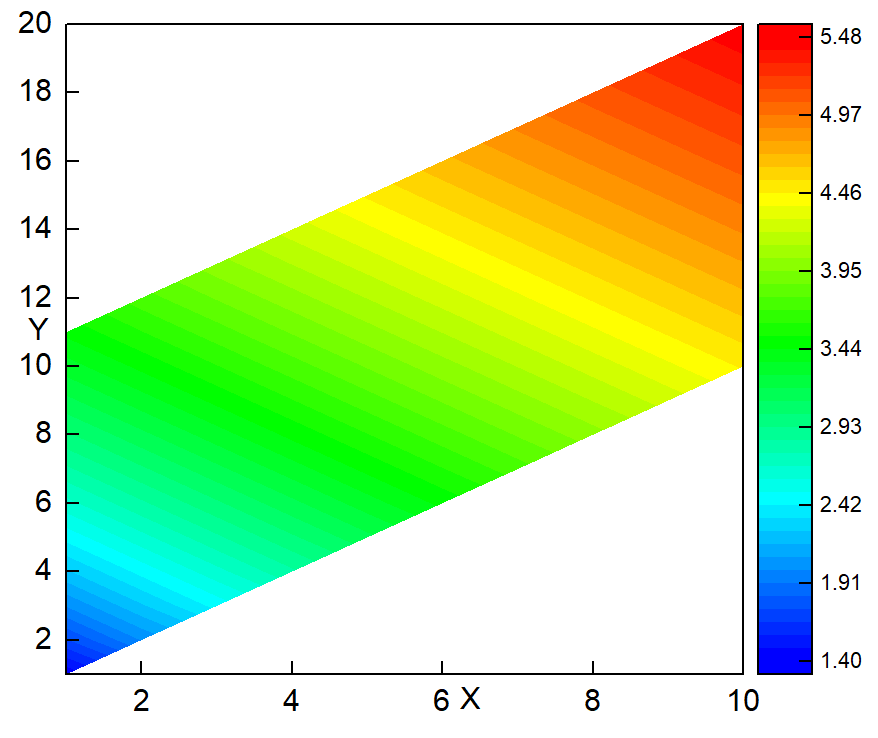
六边形区域
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! Graphene BZ plot
module pub
implicit none
complex,parameter::im = (0.0,1.0)
real,parameter::pi = 3.14159265359
integer n0 ! n0 边形
real r0 ! 外接圆半径
end module pub
!========== PROGRAM START ==========================
program sol
use pub
call BZ()
stop
end program sol
!===================================================
subroutine BZ()
use pub
real dx,dy,d0
d0 = 0.01
open(20,file="graphene-BZ.dat")
do dx = -1.0,-0.5,d0
do dy = -sqrt(3.0)*dx - sqrt(3.0),sqrt(3.0)*dx + sqrt(3.0),d0
write(20,*)dx,dy,cos(sin(dx*dy))
end do
end do
do dx = -0.5,0.5,d0
do dy = -sqrt(3.0)/2.0,sqrt(3.0)/2,d0
write(20,*)dx,dy,cos(sin(dx*dy))
end do
end do
do dx = 0.5,1.0,d0
do dy = sqrt(3.0)*dx - sqrt(3.0),-sqrt(3.0)*dx + sqrt(3.0),d0
write(20,*)dx,dy,cos(sin(dx*dy))
end do
end do
return
end subroutine BZ
绘图程序
set encoding iso_8859_1
#set terminal postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1920
set output 'density.png'
set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
#set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
#set size ratio -1
set size 1,1 # 图片比列
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-1:1]
set yrange [-1:1]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'hex.dat' u 1:2:3 w pm3d
#splot 'sq45.dat' u 1:2:3 w pm3d
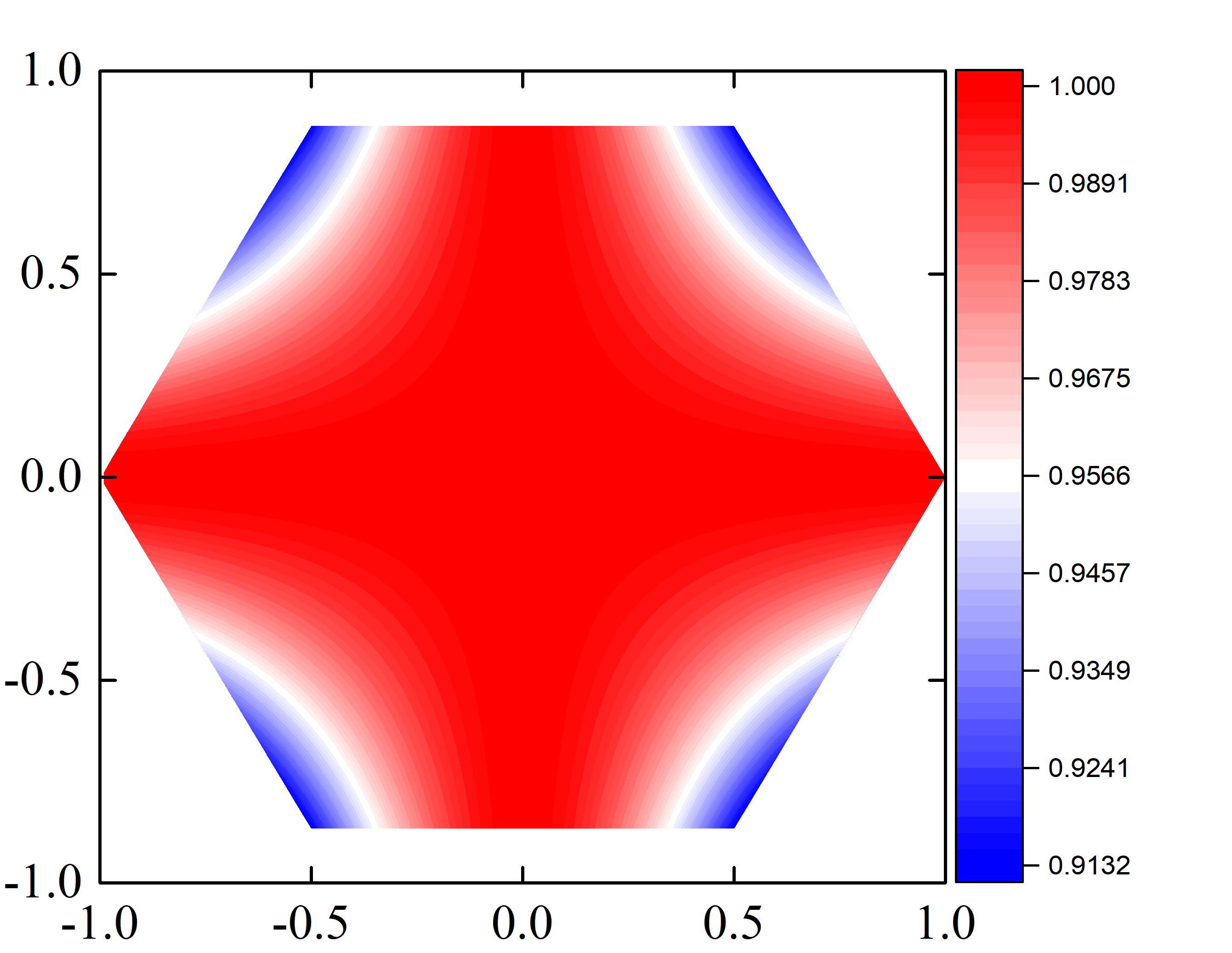
正方旋转$45^o$
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! Graphene BZ plot
module pub
implicit none
complex,parameter::im = (0.0,1.0)
real,parameter::pi = 3.14159265359
end module pub
!========== PROGRAM START ==========================
program sol
use pub
call sq45()
stop
end program sol
!============================================================================
subroutine sq45()
use pub
real dx,dy,d0,ang,k0,b0
real nx
nx = 10.0
ang = pi/4.0
d0 = 0.1
k0 = 2*sin(ang) ! 斜率
b0 = k0*nx ! 截距
open(22,file="sq45.dat")
do dx = -nx,0.0,d0
do dy = -(k0*dx + b0),k0*dx + b0,d0
write(22,*)dx,dy,cos(dx*dy)
end do
write(22,*)""
end do
do dx = 0.0,nx,d0
do dy = -(-k0*dx + b0),-k0*dx + b0,d0
write(22,*)dx,dy,cos(dx*dy)
end do
write(22,*)""
end do
close(22)
return
end subroutine sq45
因为撒点太密的话,数据文件会会比较大,此时推荐使用gnuplot绘图
set encoding iso_8859_1
#set terminal postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1920
set output 'density.png'
set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
#set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
#set size ratio -1
set size 1,1 # 图片比列
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-10:10]
set yrange [-15:15]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'sq45.dat' u 1:2:3 w pm3d
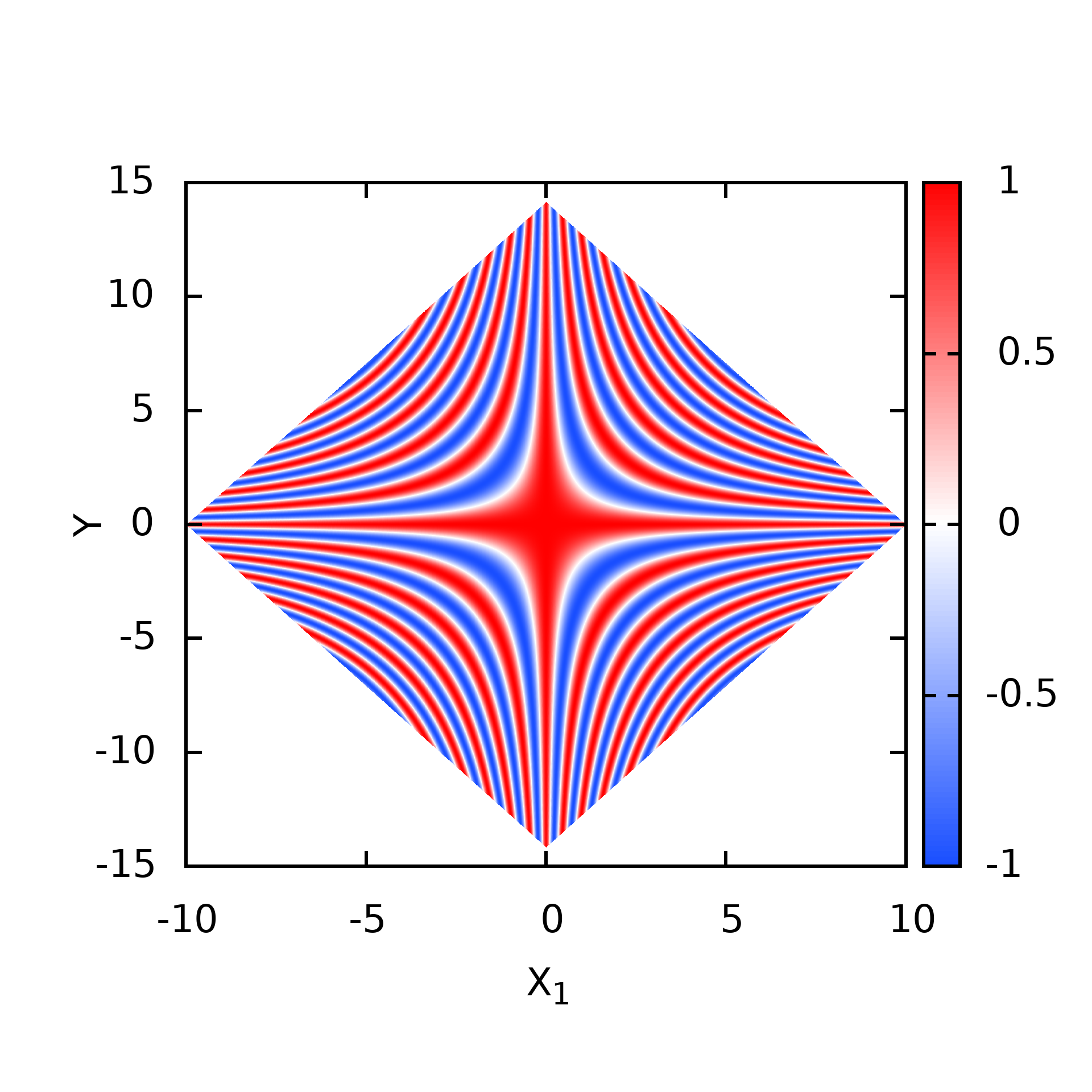
三角形点阵哈密顿量
最近遇到要在一个三角形点阵上计算一些内容,需要构建哈密顿量,主要的想法就是将三角形点阵上的index搞清楚,然后构建对应格点上哈密顿量,代码如下
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! H(k)=(m0 + tx cos kx + ty cos ky) + ax sin kx + ay sin ky
module pub
implicit none
integer xn,yn,N,len2
parameter(xn = 30,yn = 30,N = yn*(yn + 1)/2*8,len2 = yn*(yn + 1)/2)
complex,parameter::im = (0.0,1.0)
real,parameter::pi = 3.14159265359
complex Ham(N,N)
integer bry(4,len2)
real m0,mu,omega,tx,ty,del0,delx,dely,ax,ay,h0
!-------------------lapack parameter----------------------------------------
integer::lda = N
integer,parameter::lwmax = 2*N + N**2
real,allocatable::w(:)
complex*8,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork
integer lrwork
integer liwork
integer info
end module pub
!========== PROGRAM START ==========================
program sol
use pub
!================ Physics memory allocate =================
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1 + 5*N + 2*N**2))
allocate(iwork(3 + 5*N))
!--------------------
m0 = 1.5
tx = 1.0
ty = -1.0
mu = 0
ax = 1.0
ay = 1.0
omega = 0 ! LDOS
!------------- D(k) = D0 + D_x cos(k_x) + D_y cos(k_y) -
del0 = 0
delx = 0.2
dely = -delx
call cut()
! call matset()
call ldos(0.0)
stop
end program sol
!===========================================================
subroutine boundary2()
use pub
integer i,ix,iy
bry = 0
do iy = 1,yn
do ix = 1,iy
i = iy*(iy - 1)/2 + ix
bry(1,i) = i + 1 ! right hopping
if(ix.eq.iy)bry(1,i) = bry(1,i) - iy
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = bry(2,i) + iy
bry(3,i) = i + iy ! up hopping
if(iy.eq.yn)bry(3,i) = (ix + 1)*ix/2
bry(4,i)= i - (iy - 1) ! down hopping
if(iy.eq.ix)bry(4,i) = yn*(yn - 1)/2 + ix
enddo
enddo
open(10,file="index.dat")
do iy = 1,yn
do ix = 1,iy
i = iy*(iy - 1)/2 + ix
write(10,999)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
end do
end do
close(10)
999format(7I8)
return
end subroutine boundary2
!==========================================================
subroutine cut()
use pub
integer ix,iy
call boundary2()
do iy = 1,yn
do ix = 1,iy
i = iy*(iy - 1)/2 + ix
Ham(i , i) = m0 - mu
Ham(len2 + i , len2 + i) = -m0 - mu
Ham(len2*2 + i , len2*2 + i) = -m0 - mu
Ham(len2*3 + i , len2*3 + i) = m0 - mu
Ham(len2*4 + i , len2*4 + i) = -m0 + mu
Ham(len2*5 + i , len2*5 + i) = m0 + mu
Ham(len2*6 + i , len2*6 + i) = m0 + mu
Ham(len2*7 + i , len2*7 + i) = -m0 + mu
!----------------------------------------------------------
!(1,1)
if (ix.ne.iy)Ham(i,bry(1,i)) = tx/2.0
if (ix.ne.1)Ham(i,bry(2,i)) = tx/2.0
if (iy.ne.yn)Ham(i,bry(3,i)) = ty/2.0
if (iy.ne.ix)Ham(i,bry(4,i)) = ty/2.0
! if(ix.ne.iy)write(11,*)iy,ix,i,bry(1,i)
! if(ix.ne.1)write(12,*)iy,ix,i,bry(2,i)
! if(iy.ne.yn)write(13,*)iy,ix,i,bry(3,i)
! if(iy.ne.1)write(14,*)iy,ix,i,bry(4,i)
!(2,2)
if (ix.ne.iy)Ham(len2 + i, len2 + bry(1,i)) = -tx/2.0
if (ix.ne.1)Ham(len2 + i, len2 + bry(2,i)) = -tx/2.0
if (iy.ne.yn)Ham(len2 + i, len2 + bry(3,i)) = -ty/2.0
if (iy.ne.ix)Ham(len2 + i, len2 + bry(4,i)) = -ty/2.0
!(3,3)
if (ix.ne.iy)Ham(len2*2 + i, len2*2 + bry(1,i)) = -tx/2.0
if (ix.ne.1)Ham(len2*2 + i, len2*2 + bry(2,i)) = -tx/2.0
if (iy.ne.yn)Ham(len2*2 + i, len2*2 + bry(3,i)) = -ty/2.0
if (iy.ne.ix)Ham(len2*2 + i, len2*2 + bry(4,i)) = -ty/2.0
!(4,4)
if (ix.ne.iy)Ham(len2*3 + i, len2*3 + bry(1,i)) = tx/2.0
if (ix.ne.1)Ham(len2*3 + i, len2*3 + bry(2,i)) = tx/2.0
if (iy.ne.yn)Ham(len2*3 + i, len2*3 + bry(3,i)) = ty/2.0
if (iy.ne.ix)Ham(len2*3 + i, len2*3 + bry(4,i)) = ty/2.0
!(5,5)
if (ix.ne.iy)Ham(len2*4 + i, len2*4 + bry(1,i)) = -tx/2.0
if (ix.ne.1)Ham(len2*4 + i, len2*4 + bry(2,i)) = -tx/2.0
if (iy.ne.yn)Ham(len2*4 + i, len2*4 + bry(3,i)) = -ty/2.0
if (iy.ne.ix)Ham(len2*4 + i, len2*4 + bry(4,i)) = -ty/2.0
!(6,6)
if (ix.ne.iy)Ham(len2*5 + i, len2*5 + bry(1,i)) = tx/2.0
if (ix.ne.1)Ham(len2*5 + i, len2*5 + bry(2,i)) = tx/2.0
if (iy.ne.yn)Ham(len2*5 + i, len2*5 + bry(3,i)) = ty/2.0
if (iy.ne.ix)Ham(len2*5 + i, len2*5 + bry(4,i)) = ty/2.0
!(7,7)
if (ix.ne.iy)Ham(len2*6 + i, len2*6 + bry(1,i)) = tx/2.0
if (ix.ne.1)Ham(len2*6 + i, len2*6 + bry(2,i)) = tx/2.0
if (iy.ne.yn)Ham(len2*6 + i, len2*6 + bry(3,i)) = ty/2.0
if (iy.ne.ix)Ham(len2*6 + i, len2*6 + bry(4,i)) = ty/2.0
!(8,8)
if (ix.ne.iy)Ham(len2*7 + i, len2*7 + bry(1,i)) = -tx/2.0
if (ix.ne.1)Ham(len2*7 + i, len2*7 + bry(2,i)) = -tx/2.0
if (iy.ne.yn)Ham(len2*7 + i, len2*7 + bry(3,i)) = -ty/2.0
if (iy.ne.ix)Ham(len2*7 + i, len2*7 + bry(4,i)) = -ty/2.0
!=========================================================
!(1,2)
if (ix.ne.iy)Ham(i, len2 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(i, len2 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(i, len2 + bry(3,i)) = -im*ay/(2.0*im)
if (iy.ne.ix)Ham(i, len2 + bry(4,i)) = im*ay/(2.0*im)
!(2,1)
if (ix.ne.iy)Ham(len2 + i,bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2 + i,bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2 + i,bry(3,i)) = im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2 + i,bry(4,i)) = -im*ay/(2.0*im)
!(3,4)
if (ix.ne.iy)Ham(len2*2 + i, len2*3 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*2 + i, len2*3 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*2 + i, len2*3 + bry(3,i)) = -im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*2 + i, len2*3 + bry(4,i)) = im*ay/(2.0*im)
!(4,3)
if (ix.ne.iy)Ham(len2*3 + i, len2*2 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*3 + i, len2*2 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*3 + i, len2*2 + bry(3,i)) = im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*3 + i, len2*2 + bry(4,i)) = -im*ay/(2.0*im)
!(5,6)
if (ix.ne.iy)Ham(len2*4 + i, len2*5 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*4 + i, len2*5 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*4 + i, len2*5 + bry(3,i)) = im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*4 + i, len2*5 + bry(4,i)) = -im*ay/(2.0*im)
!(6,5)
if (ix.ne.iy)Ham(len2*5 + i, len2*4 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*5 + i, len2*4 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*5 + i, len2*4 + bry(3,i)) = -im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*5 + i, len2*4 + bry(4,i)) = im*ay/(2.0*im)
!(7.8)
if (ix.ne.iy)Ham(len2*6 + i, len2*7 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*6 + i, len2*7 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*6 + i, len2*7 + bry(3,i)) = im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*6 + i, len2*7 + bry(4,i)) = -im*ay/(2.0*im)
!(8,7)
if (ix.ne.iy)Ham(len2*7 + i, len2*6 + bry(1,i)) = ax/(2.0*im)
if (ix.ne.1)Ham(len2*7 + i, len2*6 + bry(2,i)) = -ax/(2.0*im)
if (iy.ne.yn)Ham(len2*7 + i, len2*6 + bry(3,i)) = -im*ay/(2.0*im)
if (iy.ne.ix)Ham(len2*7 + i, len2*6 + bry(4,i)) = im*ay/(2.0*im)
!============================================
!(1,7)
Ham(i, len2*6 + i) = -del0
if (ix.ne.iy)Ham(i, len2*6 + bry(1,i)) = -delx
if (ix.ne.1)Ham(i, len2*6 + bry(2,i)) = -delx
if (iy.ne.yn)Ham(i, len2*6 + bry(3,i)) = -dely
if (iy.ne.ix)Ham(i, len2*6 + bry(4,i)) = -dely
!(2,8)
Ham(len2 + i, len2*7 + i) = -del0
if (ix.ne.iy)Ham(len2 + i, len2*7 + bry(1,i)) = -delx
if (ix.ne.1)Ham(len2 + i, len2*7 + bry(2,i)) = -delx
if (iy.ne.yn)Ham(len2 + i, len2*7 + bry(3,i)) = -dely
if (iy.ne.ix)Ham(len2 + i, len2*7 + bry(4,i)) = -dely
!(3,5)
Ham(len2*2 + i, len2*4 + i) = del0
if (ix.ne.iy)Ham(len2*2 + i, len2*4 + bry(1,i)) = delx
if (ix.ne.1)Ham(len2*2 + i, len2*4 + bry(2,i)) = delx
if (iy.ne.yn)Ham(len2*2 + i, len2*4 + bry(3,i)) = dely
if (iy.ne.ix)Ham(len2*2 + i, len2*4 + bry(4,i)) = dely
!(4,6)
Ham(len2*3 + i, len2*5 + i) = del0
if (ix.ne.iy)Ham(len2*3 + i, len2*5 + bry(1,i)) = delx
if (ix.ne.1)Ham(len2*3 + i, len2*5 + bry(2,i)) = delx
if (iy.ne.yn)Ham(len2*3 + i, len2*5 + bry(3,i)) = dely
if (iy.ne.ix)Ham(len2*3 + i, len2*5 + bry(4,i)) = dely
!(7,1)
Ham(len2*6 + i,i) = -del0
if (ix.ne.iy)Ham(len2*6 + i,bry(1,i)) = -delx
if (ix.ne.1)Ham(len2*6 + i,bry(2,i)) = -delx
if (iy.ne.yn)Ham(len2*6 + i,bry(3,i)) = -dely
if (iy.ne.ix)Ham(len2*6 + i,bry(4,i)) = -dely
!(8,2)
Ham(len2*7 + i,len2 + i) = -del0
if (ix.ne.iy)Ham(len2*7 + i, len2 + bry(1,i)) = -delx
if (ix.ne.1)Ham(len2*7 + i, len2 + bry(2,i)) = -delx
if (iy.ne.yn)Ham(len2*7 + i, len2 + bry(3,i)) = -dely
if (iy.ne.ix)Ham(len2*7 + i, len2 + bry(4,i)) = -dely
!(5,3)
Ham(len2*4 + i,len2*2 + i) = del0
if (ix.ne.iy)Ham(len2*4 + i, len2*2 + bry(1,i)) = delx
if (ix.ne.1)Ham(len2*4 + i, len2*2 + bry(2,i)) = delx
if (iy.ne.yn)Ham(len2*4 + i, len2*2 + bry(3,i)) = dely
if (iy.ne.ix)Ham(len2*4 + i, len2*2 + bry(4,i)) = dely
!(6,4)
Ham(len2*5 + i,len*3 + i) = del0
if (ix.ne.iy)Ham(len2*5 + i, len2*3 + bry(1,i)) = delx
if (ix.ne.1)Ham(len2*5 + i, len2*3 + bry(2,i)) = delx
if (iy.ne.yn)Ham(len2*5 + i, len2*3 + bry(3,i)) = dely
if (iy.ne.ix)Ham(len2*5 + i, len2*3 + bry(4,i)) = dely
end do
end do
!--------------------------------------
call isHermitian()
call eigsol()
return
end subroutine
!===========================Local Density of State=============================
subroutine ldos(omg)
use pub
integer m,l1,k,l2
real s,omg
real,external::delta
open(12,file="ldos.dat")
do l1 = 1,yn
do l2 = 1,l1
k = l1*(l1 - 1)/2 + l2
s = 0
do m=1,N
s = s + delta(w(m) - omg)*(abs(Ham(k , m))**2 + abs(Ham(k + len2 , m))**2)&
+ delta(w(m) - omg)*(abs(Ham(k + len2*6 , m))**2 + abs(Ham(k + len2*7 , m))**2)
end do
write(12,*)l1,l2,s
end do
end do
close(12)
return
end subroutine ldos
!======================================================================
real function delta(x)
real x
real::gamma = 0.001
delta = 1.0/3.1415926535*gamma/(x*x + gamma*gamma)
end function delta
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(160,file = 'hermitian.dat')
write(160,*)i,j
write(160,*)Ham(i,j)
write(160,*)Ham(j,i)
write(*,*)"Hamiltonian is not Hermitian"
stop
end if
end do
end do
close(160)
return
end subroutine isHermitian
!================= Hermitain Matrices solve ==============
subroutine eigsol(input)
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(110,file="mes.dat",status="unknown")
write(110,*)'The algorithm failed to compute eigenvalues.'
close(110)
end if
open(120,file = "eigval.dat")
do m = 1,N
write(120,*)m,w(m)
end do
close(120)
return
end subroutine eigsol
这里重要的部分就是
subroutine boundary2()
use pub
integer i,ix,iy
bry = 0
do iy = 1,yn
do ix = 1,iy
i = iy*(iy - 1)/2 + ix
bry(1,i) = i + 1 ! right hopping
if(ix.eq.iy)bry(1,i) = bry(1,i) - iy
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = bry(2,i) + iy
bry(3,i) = i + iy ! up hopping
if(iy.eq.yn)bry(3,i) = (ix + 1)*ix/2
bry(4,i)= i - (iy - 1) ! down hopping
if(iy.eq.ix)bry(4,i) = yn*(yn - 1)/2 + ix
enddo
enddo
open(10,file="index.dat")
do iy = 1,yn
do ix = 1,iy
i = iy*(iy - 1)/2 + ix
write(10,999)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
end do
end do
close(10)
999format(7I8)
return
end subroutine boundary2
这里就构建了一个下三角点阵,而且使用了周期边界条件.
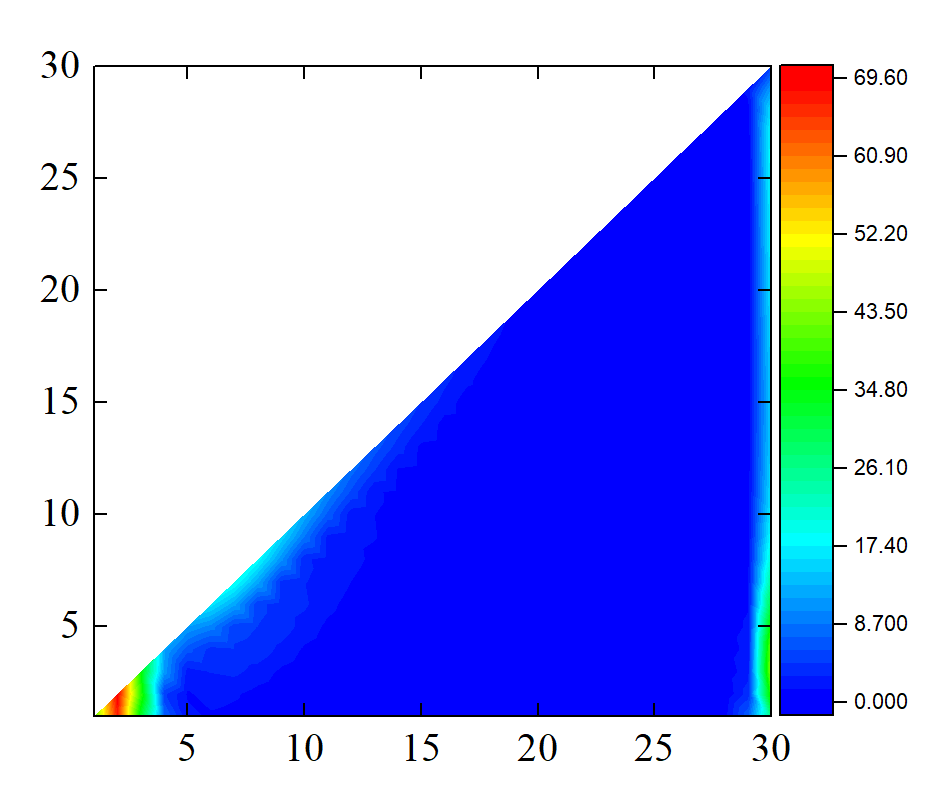
矩形点阵哈密顿量格点
这里尝试构建开边界条件
module pub
implicit none
integer yn,xn,yn1,len2,N
real pi
complex im
parameter(yn = 10,yn1 = 10,len2 = yn*yn,N = len2 + 2*yn*(yn + 1)/2,pi=3.1415926535,im = (0.0,1.0))
integer bry(4,len2 + 2*yn*(yn + 1)/2)
real tx,ty,ax,ay
complex Ham(N,N)
end module pub
!=================================================
program sol
use pub
tx = 1.0
ty = 1.0
ax = 1.0
ay = 1.0
write(*,*)N
write(*,*)tx,ty,ax,ay,im
call matset()
end program sol
!===================================================
subroutine lattice()
! 开边界条件
use pub
integer ix,iy,i
i = 0
! ! 下三角
do iy = 1,yn1
do ix = 1,iy
! i = iy*(iy - 1)/2 + ix
i = i + 1
bry(1,i) = i + 1 ! right hopping
if(ix.eq.iy)bry(1,i) = 0
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = 0
bry(3,i) = i + iy ! up hopping
if(iy.eq.yn1)bry(3,i) = 0
bry(4,i)= i - (iy - 1) ! down hopping
if(iy.eq.ix)bry(4,i) = 0
enddo
enddo
! ! 矩形
do iy = 1,yn
do ix = 1,yn
! i = yn1*(yn1 + 1)/2 + (iy - 1)*yn + ix
i = i + 1
bry(1,i) = i + 1 !right hopping
if(ix.eq.xn)bry(1,i) = 0
bry(2,i) = i - 1 !left hopping
if(ix.eq.xn)bry(2,i) = 0
bry(3,i) = i + yn !up hopping
if(iy.eq.yn)bry(3,i) = 0
bry(4,i) = i - yn !down hopping
if(iy.eq.1)bry(4,i) = 0
end do
end do
! ! 上三角
! i = yn1*(yn1 + 1)/2 + yn*yn
! i = 0
do iy = 1,yn
do ix = 1,yn - (iy - 1)
i = i + 1
bry(1,i) = i + 1 ! right hopping
if(ix.eq.yn - (iy - 1))bry(1,i) = 0
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = 0
bry(3,i) = i + yn - iy ! up hopping
if(iy.eq.ix)bry(3,i) = 0
bry(4,i) = i - (yn - iy) ! down hopping
if(iy.eq.1)bry(4,i) = 0
end do
end do
open(10,file="pall.dat")
do i = 1,N
write(10,888)i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
end do
close(10)
888 format(8I8)
return
end subroutine lattice
!=========================================================================
subroutine matset()
use pub
integer i
call lattice()
do i = 1,N
if(bry(1,i).ne.0)ham(i,bry(1,i)) = ax/(2.0*im)
if(bry(2,i).ne.0)ham(i,bry(2,i)) = -ax/(2.0*im)
if(bry(3,i).ne.0)ham(i,bry(3,i)) = im*ay/(2.0*im)
if(bry(4,i).ne.0)ham(i,bry(4,i)) = -im*ay/(2.0*im)
end do
!-------------------------------------
call isHermitian()
return
end subroutine
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(160,file = 'hermitian.dat')
write(160,*)i,j
write(160,*)Ham(i,j)
write(160,*)Ham(j,i)
write(*,*)"Hamiltonian is not Hermitian"
stop
end if
end do
end do
close(160)
return
end subroutine isHermitian
这里想再利用同样的方式构造矩形点阵的哈密顿量,先进行了简单的尝试(尝试周期性边界条件),暂时未完成.
module pub
implicit none
integer yn,xn,yn1,len2
parameter(yn = 10,yn1 = 10,len2 = yn*yn)
integer bry(4,len2 + 2*yn*(yn + 1)/2)
end module pub
!=================================================
program sol
use pub
call lattice()
end program sol
!===================================================
subroutine lattice()
use pub
integer ix,iy,i
! ! 下三角
! do iy = 1,yn1
! do ix = 1,iy
! i = iy*(iy - 1)/2 + ix
! bry(1,i) = i + 1 ! right hopping
! if(ix.eq.iy)bry(1,i) = bry(1,i) - iy
! bry(2,i) = i - 1 ! left hopping
! if(ix.eq.1)bry(2,i) = bry(2,i) + iy
! bry(3,i) = i + iy ! up hopping
! if(iy.eq.yn1)bry(3,i) = (ix + 1)*ix/2
! bry(4,i)= i - (iy - 1) ! down hopping
! if(iy.eq.ix)bry(4,i) = yn1*(yn1 - 1)/2 + ix
! enddo
! enddo
! ! 矩形
! do iy = 1,yn
! do ix = 1,yn
! i = yn1*(yn1 + 1)/2 + (iy - 1)*yn + ix
! bry(1,i) = i + 1 !right hopping
! if(ix.eq.xn)bry(1,i) = bry(1,i) - xn
! bry(2,i) = i - 1 !left hopping
! if(ix.eq.xn)bry(2,i) = bry(2,i) + xn
! bry(3,i) = i + yn !up hopping
! if(iy.eq.yn)bry(3,i) = bry(3,i) - len2
! bry(4,i) = i - yn !down hopping
! if(iy.eq.1)bry(4,i) = bry(4,i) + len2
! end do
! end do
! ! 上三角
! i = yn1*(yn1 + 1)/2 + yn*yn
do iy = 1,yn
do ix = 1,yn - (iy - 1)
i = i + 1
bry(1,i) = i + 1 ! right hopping
if(ix.eq.yn - iy - 1)bry(1,i) = bry(1,i) - (yn - iy) + 1
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = bry(2,i) + (yn - iy) + 1
bry(3,i) = i + yn - iy ! up hopping
if(iy.eq.ix)bry(3,i) = bry(3,i) - (yn - iy) + (ix-iy)*(yn - iy)
bry(4,i) = i - (yn - iy) ! down hopping
if(iy.eq.1)bry(4,i) = i + yn*(yn + 1)/2 - (yn - iy - 1)*(yn - iy + 1 + 1)/2 + 1
end do
end do
open(10,file="up_triangle.dat")
i = 0
do iy = 1,yn
do ix = 1,yn - (iy - 1)
i = i + 1
write(10,888)iy,ix,i,bry(1,i),bry(2,i),bry(3,i),bry(4,i)
end do
end do
close(10)
888 format(8I8)
return
end subroutine lattice
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |