PythonTB学习笔记
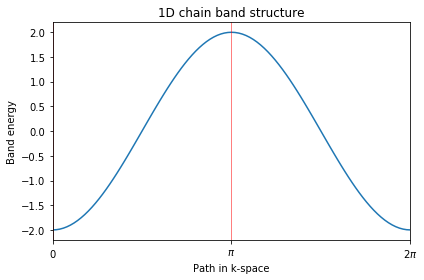
简单一维模型求解
1 | #!/usr/bin/env python |
Path in 1D BZ defined by nodes at [0. 0.5 1. ]
二维模型求解
1 | #!/usr/bin/env python |
----- k_path report begin ----------
real-space lattice vectors
[[1. 0.]
[0. 1.]]
k-space metric tensor
[[1. 0.]
[0. 1.]]
internal coordinates of nodes
[[0. 0. ]
[0. 0.5]
[0.5 0.5]
[0. 0. ]]
reciprocal-space lattice vectors
[[1. 0.]
[0. 1.]]
cartesian coordinates of nodes
[[0. 0. ]
[0. 0.5]
[0.5 0.5]
[0. 0. ]]
list of segments:
length = 0.5 from [0. 0.] to [0. 0.5]
length = 0.5 from [0. 0.5] to [0.5 0.5]
length = 0.70711 from [0.5 0.5] to [0. 0.]
node distance list: [0. 0.5 1. 1.70711]
node index list: [ 0 88 176 300]
----- k_path report end ------------
---------------------------------------
starting calculation
---------------------------------------
Calculating bands...
Plotting bandstructure...
Done.
1 | #!/usr/bin/env python |
Path in 1D BZ defined by nodes at [-0.5 0. 0.5]
---------------------------------------
starting calculation
---------------------------------------
Calculating bands...
Plotting bandstructure...
Done.
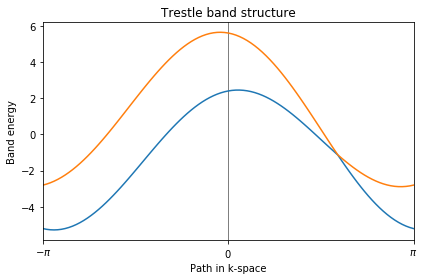
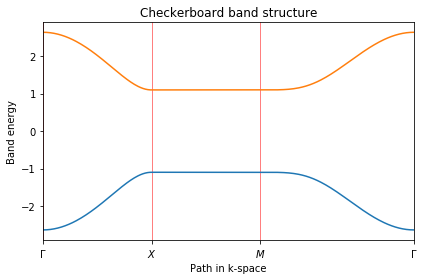
从能带的计算结果就可以看到,在构建模型的时候,每个元胞中是有两个轨道的,如果认为每个轨道来自不同的原子的话,也就是每个元胞中都是由2个原子的
1 | #!/usr/bin/env python |
---------------------------------------
starting calculation
---------------------------------------
Calculating bands...
Band energies
Done.
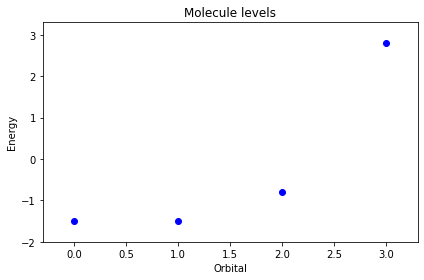
从计算结果也可以清楚的看到,一个分子中,也可以认为是一个元胞中有4个TB轨道,所以对于单分子进行求解之后,也就只有4个能量本征值
Graphene model
1 | #!/usr/bin/env python |
----- k_path report begin ----------
real-space lattice vectors
[[1. 0. ]
[0.5 0.86603]]
k-space metric tensor
[[ 1.33333 -0.66667]
[-0.66667 1.33333]]
internal coordinates of nodes
[[0. 0. ]
[0.66667 0.33333]
[0.5 0.5 ]
[0. 0. ]]
reciprocal-space lattice vectors
[[ 1. -0.57735]
[ 0. 1.1547 ]]
cartesian coordinates of nodes
[[0. 0. ]
[0.66667 0. ]
[0.5 0.28868]
[0. 0. ]]
list of segments:
length = 0.66667 from [0. 0.] to [0.66667 0.33333]
length = 0.33333 from [0.66667 0.33333] to [0.5 0.5]
length = 0.57735 from [0.5 0.5] to [0. 0.]
node distance list: [0. 0.66667 1. 1.57735]
node index list: [ 0 51 76 120]
----- k_path report end ------------
---------------------------------------
starting calculation
---------------------------------------
Calculating bands...
Done.
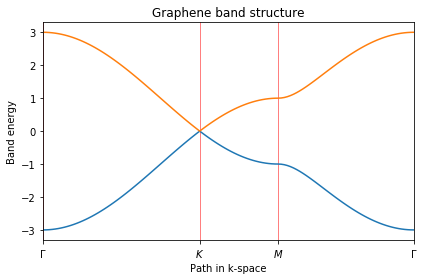
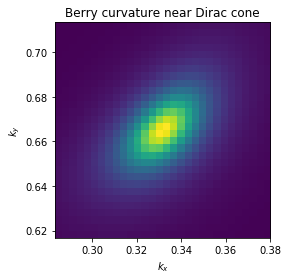
Berry phase around Dirac cone in graphene
1 | #!/usr/bin/env python |
Berry phase along circle with radius: 0.05
centered at k-point: [0.33333333 0.66666667]
for band 0 equals : 2.068204018990522
for band 1 equals : -2.068204018990522
for both bands equals: 3.469446951953614e-17
Berry flux on square patch with length: 0.1
centered at k-point: [0.33333333 0.66666667]
for band 0 equals : 2.179216480131516
for band 1 equals : -2.1792164801315166
for both bands equals: 3.308776163370093e-16
Done.
One-dimensional cycle of 1D tight-binding model
1 | #!/usr/bin/env python |
Berry flux in k-lambda space: -6.283185307179586
Done.
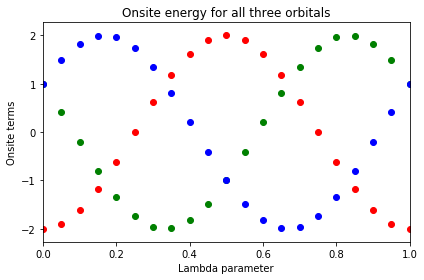
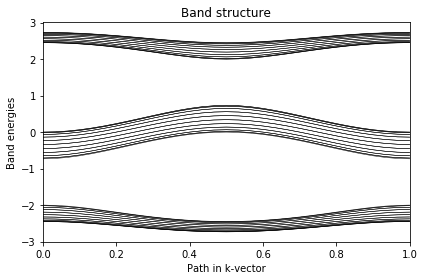
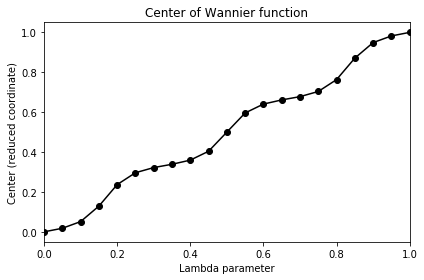
One-dimensional cycle on a finite 1D chain
1 | #!/usr/bin/env python |
Chern numbers for rising fillings
Band 0 = 1.00
Bands 0,1 = -1.00
Bands 0,1,2 = -0.00
Chern numbers for individual bands
Band 0 = 1.00
Band 1 = -2.00
Band 2 = 1.00
Done.
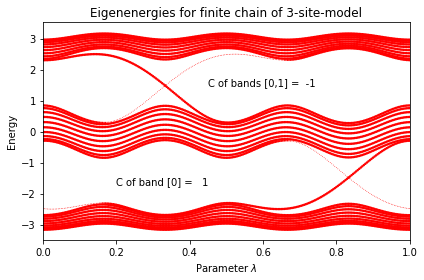
Haldane model
1 | #!/usr/bin/env python |
----- k_path report begin ----------
real-space lattice vectors
[[1. 0. ]
[0.5 0.86603]]
k-space metric tensor
[[ 1.33333 -0.66667]
[-0.66667 1.33333]]
internal coordinates of nodes
[[0. 0. ]
[0.66667 0.33333]
[0.5 0.5 ]
[0.33333 0.66667]
[0. 0. ]]
reciprocal-space lattice vectors
[[ 1. -0.57735]
[ 0. 1.1547 ]]
cartesian coordinates of nodes
[[0. 0. ]
[0.66667 0. ]
[0.5 0.28868]
[0.33333 0.57735]
[0. 0. ]]
list of segments:
length = 0.66667 from [0. 0.] to [0.66667 0.33333]
length = 0.33333 from [0.66667 0.33333] to [0.5 0.5]
length = 0.33333 from [0.5 0.5] to [0.33333 0.66667]
length = 0.66667 from [0.33333 0.66667] to [0. 0.]
node distance list: [0. 0.66667 1. 1.33333 2. ]
node index list: [ 0 33 50 67 100]
----- k_path report end ------------
---------------------------------------
starting DOS calculation
---------------------------------------
Calculating DOS...
Plotting DOS...
Done.
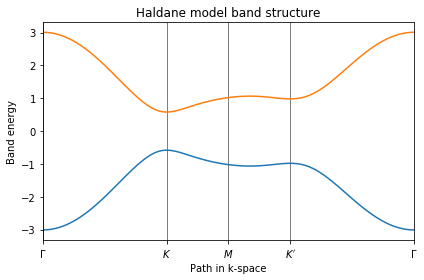
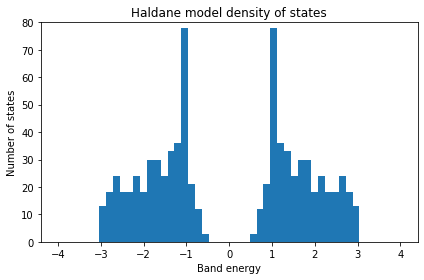
Finite Haldane model
1 | #!/usr/bin/env python |
Done.
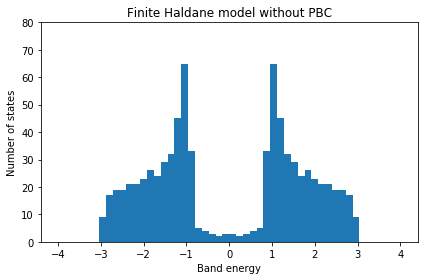
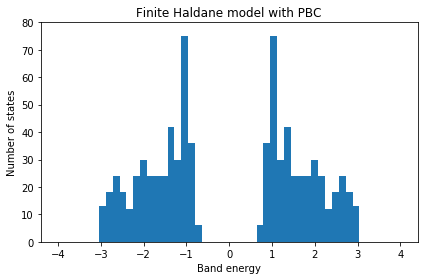
Edge states
1 | #!/usr/bin/env python |
Done.
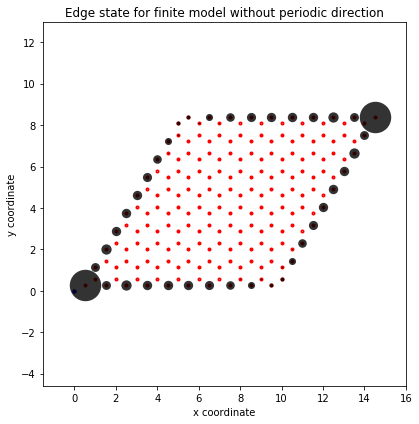

Berry phases in Haldane model
1 | #!/usr/bin/env python |
Using approach #1
Berry flux= -6.283185307179586
Using approach #2
Berry flux= -6.283185307179586
Done.
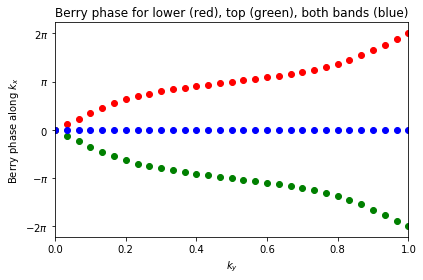
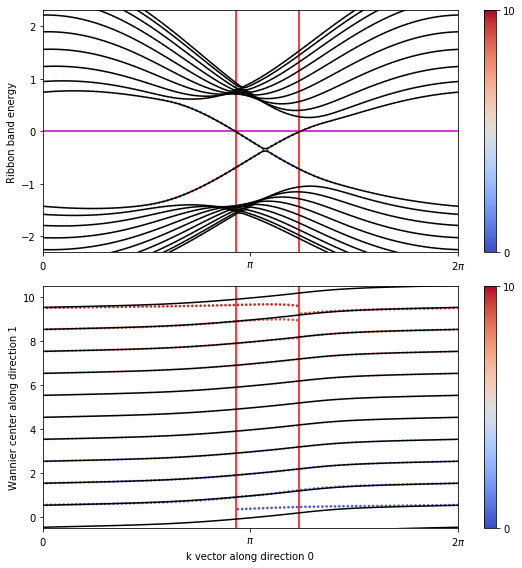
Hybrid Wannier centers in Haldane model
1 | #!/usr/bin/env python |
Done.
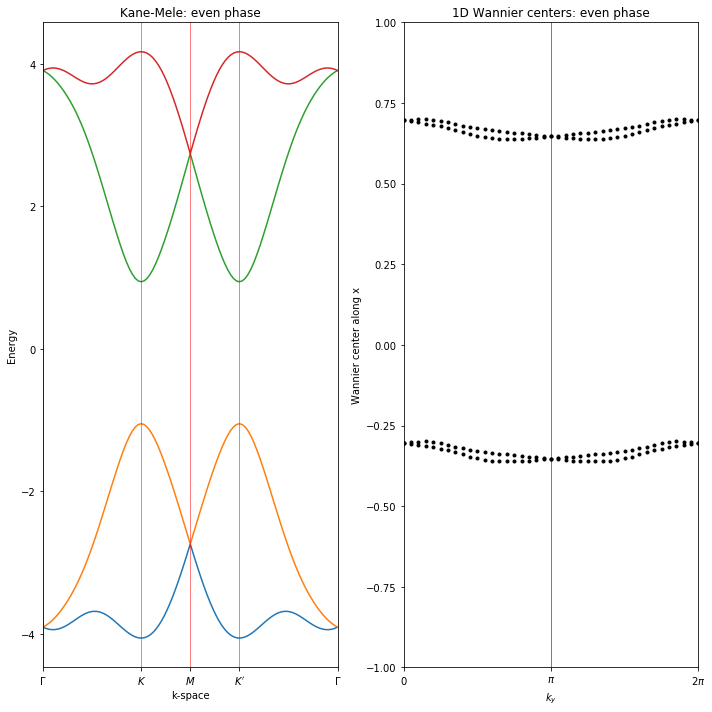
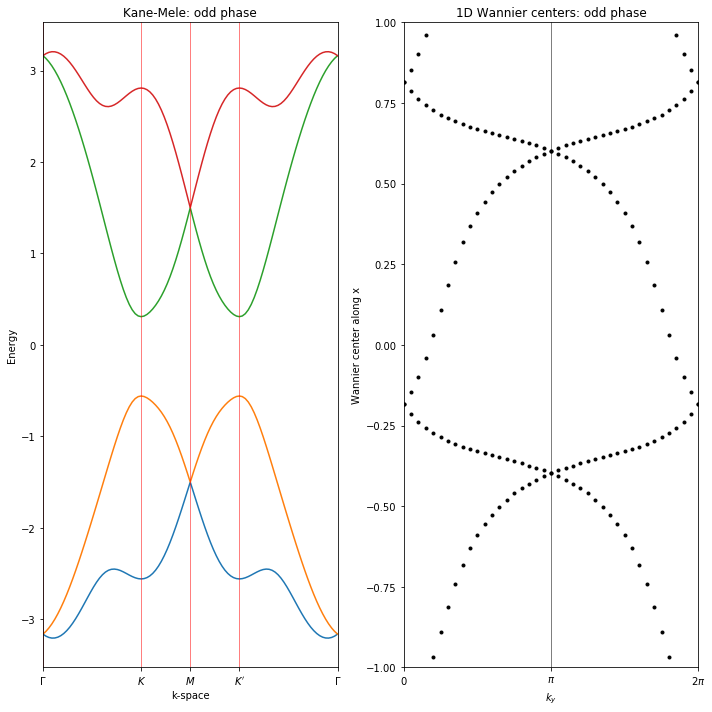
Kane-Mele model using spinor features
1 | #!/usr/bin/env python |
Done.
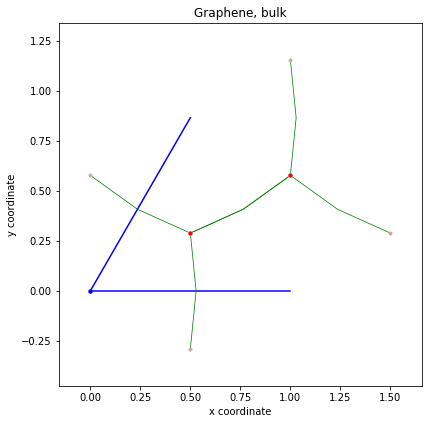
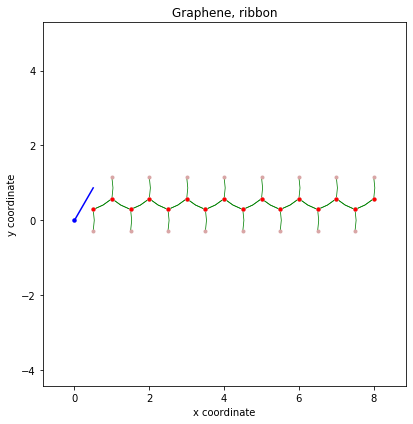
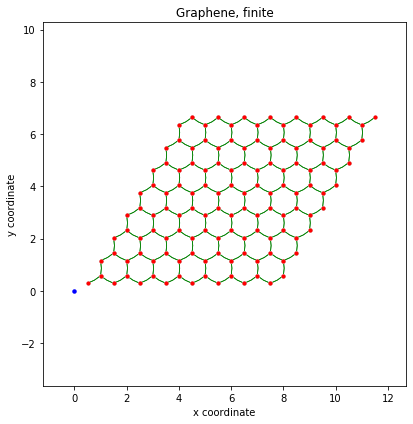
Visualization example
1 | #!/usr/bin/env python |
Done.
鉴于该网站分享的大都是学习笔记,作者水平有限,若发现有问题可以发邮件给我
- yxliphy@gmail.com
也非常欢迎喜欢分享的小伙伴投稿
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Yu-Xuan's Blog!
评论







![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

