Chern Insulator边界态及Chern数计算
虽然之前也整理了如何计算Chern数和$Z_2$拓扑不变量,但是对于最简单的Chern Insulator却没有认真的研究过,最近在做一些和反常量子霍尔相关的一些内容,就正好把这个最简单的Chern绝缘体模型的边界态以及Chern数计算的结果整理到一起.
{:.info}
边界态计算
Chern Insulator的哈密顿量非常简单
在这里写成$(m_0-t_x\cos(k_x)+t_y\cos(k_y))$的形式是为了破坏旋转对称性,这样的画采用cylinder geometry(一个方向开边界,一个方向周期)画能带图的时候,就会发现$x$方向和$y$方向的边界态一个出现的$k_{x/y}=0$,另外一个方向的边界态出现在$k_{y/x}=\pi$的位置上,如下图所示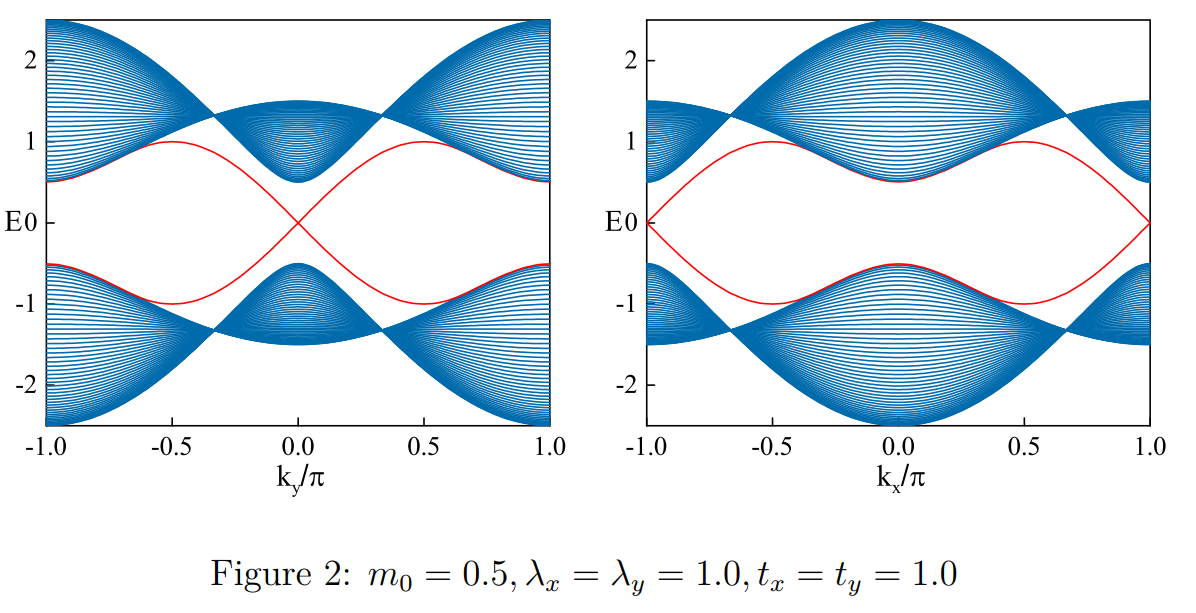
计算代码如下,之前算这东西吸怪用Fortran了,所以就一直沿用原来的习惯了,不好改过来1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192! Author: YuXuanLi
! Email:yxli406@gmail.com
module pub
implicit none
integer yn,kn,hnn
parameter(yn = 50,kn = 60,hnn = 2)
integer,parameter::N = yn*hnn
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0)
complex::Ham(N,N) = 0
complex g1(hnn,hnn),g2(hnn,hnn),g3(hnn,hnn)
!=================================
real m0,tx,ty,lamx,lamy
!================cheevd===============
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork
integer lrwork
integer liwork
integer info
end module pub
!============================================================
program sol
use pub
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
!------------------------------------
m0 = 0.5
tx = 1.0
ty = -1.0
lamx = 1.0
lamy = 1.0
call main1()
stop
end program sol
!============================================================
subroutine main1()
use pub
integer m1
real k
open(3,file="openx-m1.dat")
open(4,file="openy-m1.dat")
do m1 = -kn,kn
k = pi*m1/kn
call openx(k)
write(3,999)k/pi,(w(i),i = 1,N)
call openy(k)
write(4,999)k/pi,(w(i),i = 1,N)
end do
close(3)
close(4)
999 format(201f11.6)
end subroutine main1
!============================================================
subroutine openx(ky)
use pub
real ky
call pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hnn
do l = 1,hnn
Ham(m,l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(m,l + hnn) = tx/2.0*g3(m,l) + lamx/(2*im)*g1(m,l)
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hnn
do l = 1,hnn
Ham(k*hnn + m,k*hnn + l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = tx/2.0*g3(m,l) - lamx/(2*im)*g1(m,l)
end do
end do
else
do m = 1,hnn
do l = 1,hnn ! k start from 1,matrix block from 2th row
Ham(k*hnn + m,k*hnn + l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(k*hnn + m,k*hnn + l + hnn) = tx/2.0*g3(m,l) + lamx/(2*im)*g1(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = tx/2.0*g3(m,l) - lamx/(2*im)*g1(m,l)
end do
end do
end if
end do
!------------------------
call isHermitian()
call eigsol()
return
end subroutine openx
!============================================================
subroutine openy(kx)
use pub
real kx
call pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hnn
do l = 1,hnn
Ham(m,l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(m,l + hnn) = lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hnn
do l = 1,hnn
Ham(k*hnn + m,k*hnn + l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = -lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
else
do m = 1,hnn
do l = 1,hnn ! k start from 1,matrix block from 2th row
Ham(k*hnn + m,k*hnn + l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(k*hnn + m,k*hnn + l + hnn) = lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = -lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
end if
end do
!------------------------
call isHermitian()
call eigsol()
return
end subroutine openy
!============================================================
subroutine pauli()
use pub
g1(1,hnn) = 1
g1(2,1) = 1
!-----------------
g2(1,hnn) = -im
g2(2,1) = im
!---------------
g3(1,1) = 1
g3(2,2) = -1
end subroutine pauli
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(16,file = 'hermitian.dat')
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
write(16,*)"===================="
write(*,*)"Ham isn't Hermitian"
stop
end if
end do
end do
close(16)
return
end subroutine isHermitian
!================= 矩阵本征值求解 ==============
subroutine eigSol()
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.dat",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine eigSol
Chern Number计算
陈数的计算公式在这里就不赘述了,模型也有了,直接上代码和结果,具体想看到底是怎么算Chern的,可以参考两种方法计算Chern Number这篇文章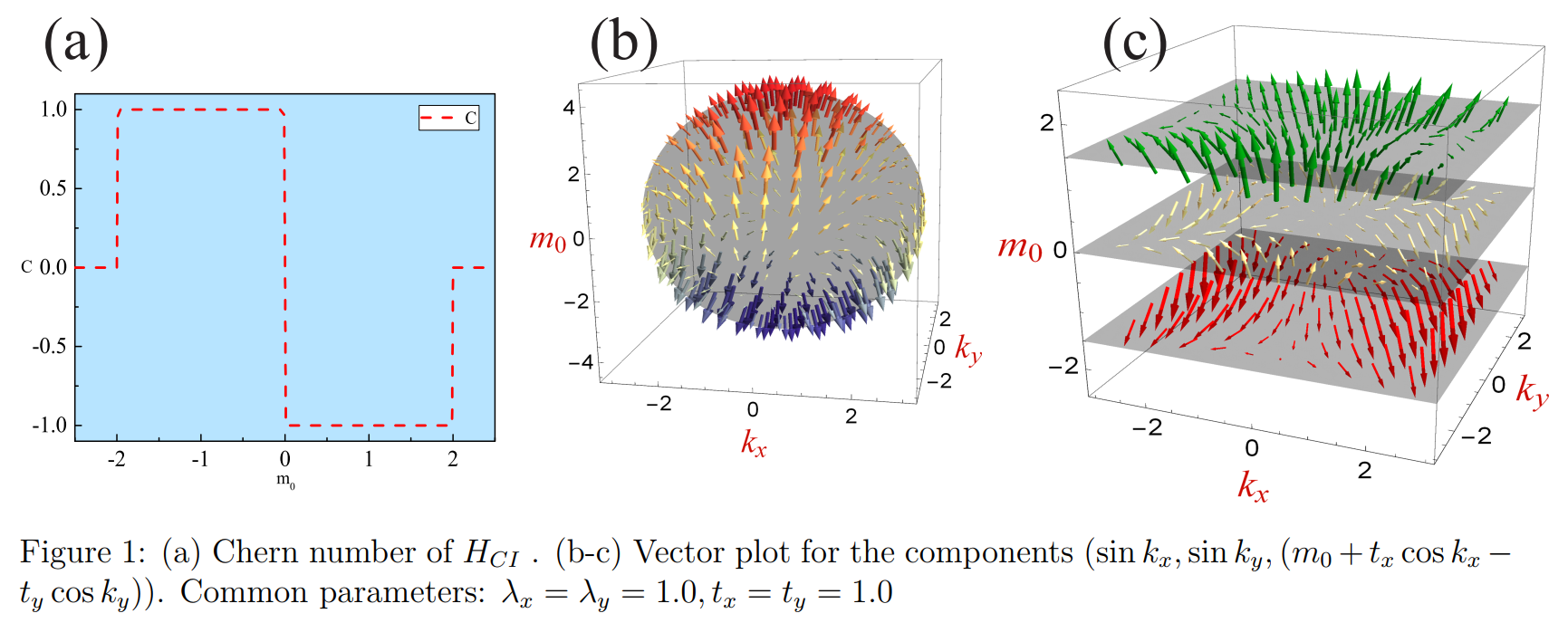
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88using LinearAlgebra,PyPlot,DelimitedFiles
# -----------------------------------------------------------------------
function matSet(kx::Float64,ky::Float64,m0::Float64)::Matrix{ComplexF64}
#m0::Float64 = 0.5
tx::Float64 = 1.0
ty::Float64 = -1.0
lamx::Float64 = 1.0
lamy::Float64 = 1.0
ham = zeros(ComplexF64,2,2)
ham[1,1] = (m0 + tx*cos(kx) + ty*cos(ky))
ham[2,2] = -(m0 + tx*cos(kx) + ty*cos(ky))
ham[1,2] = lamx*sin(kx) - 1im*lamy*sin(ky)
ham[2,1] = conj(ham[1,2])
return ham
end
#--------------------------------------------------------------------------
function ux(kx::Float64,ky::Float64,ne::Int64,m0::Float64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky,m0))[:,1]
#-----
wx = eigvecs(matSet(kx + del,ky,m0))[:,1]
#------
return w0'*wx/abs(w0'*wx)
end
#---------------------------------------------------------------------------
function uy(kx::Float64,ky::Float64,ne::Int64,m0::Float64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky,m0))[:,1]
#-----
wy = eigvecs(matSet(kx,ky + del,m0))[:,1]
#------
return w0'*wy/abs(w0'*wy)
end
#---------------------------------------------------------------------------
function img1(xlist::Array{Float64},ylist::Array{Float64},zlist::Array{ComplexF64})
zlist = map(imag,zlist)
#p1 = scatter(xlist,ylist,zlist*20,c=zlist*0.1,edgecolors="b",cmap="Reds")
p1 = scatter(xlist,ylist,zlist*200,c=zlist,cmap="Reds")
colorbar(p1)
xlabel("kx")
ylabel("ky")
title("Berry Curvature")
savefig("Berry Curature.png",bbox_inches="tight",dpi=60)
end
#----------------------------------------------------------------------------
function ChernNumber(m0::Float64)
ne::Int64 = 100
del::Float64 = pi/ne
kx::Float64 = 0.0
ky::Float64 = 0.0
flux::ComplexF64 = 0.0 + 0.0im
chern_num::ComplexF64 = 0.0 + 0.0im
kxlist = Float64[]
kylist = Float64[]
flist = ComplexF64[]
for m1 = -ne:ne
kx = m1*pi/ne
for m2 = -ne:ne
append!(kxlist,kx)
ky = m2*pi/ne
append!(kylist,ky)
flux = log((ux(kx,ky,ne,m0)*uy(kx + del,ky,ne,m0))/(ux(kx,ky + del,ne,m0)*uy(kx,ky,ne,m0)))
append!(flist,flux)
chern_num = chern_num + flux
end
end
#img1(kxlist,kylist,flist)
return round(real(chern_num/(2.0*pi*1im)))
end
#--------------------------------------------
function main1()
ch::Float64 = 0.0
chlist = []
plist = []
f1 = open("chern.dat","w")
for m0 in -2.5:0.01:2.5
ch = ChernNumber(m0)
append!(chlist,ch)
append!(plist,m0)
writedlm(f1,[m0 ch])
end
close(f1)
#plot(plist,chlist)
end
# =============================================
main1()
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |









