虽然之前也整理了如何计算Chern数和$Z_2$拓扑不变量,但是对于最简单的Chern Insulator却没有认真的研究过,最近在做一些和反常量子霍尔相关的一些内容,就正好把这个最简单的Chern绝缘体模型的边界态以及Chern数计算的结果整理到一起.
边界态计算
Chern Insulator的哈密顿量非常简单
\(\begin{equation}
H(\mathbf{k})=(m_0-t_x\cos(k_x)+t_y\cos(k_y))\sigma_z+\lambda_x\sin(k_x)+\lambda_y\sin(k_y)
\end{equation}\)
在这里写成$(m_0-t_x\cos(k_x)+t_y\cos(k_y))$的形式是为了破坏旋转对称性,这样的画采用cylinder geometry(一个方向开边界,一个方向周期)画能带图的时候,就会发现$x$方向和$y$方向的边界态一个出现的$k_{x/y}=0$,另外一个方向的边界态出现在$k_{y/x}=\pi$的位置上,如下图所示
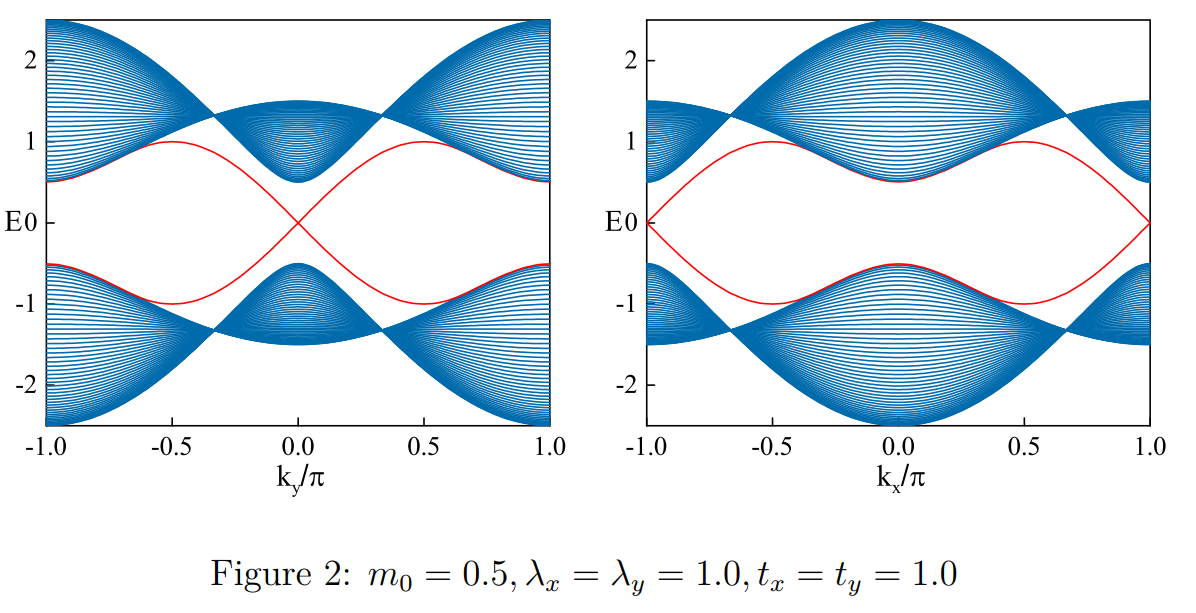
计算代码如下,之前算这东西吸怪用Fortran了,所以就一直沿用原来的习惯了,不好改过来
! Author: YuXuanLi
! Email:yxli406@gmail.com
module pub
implicit none
integer yn,kn,hnn
parameter(yn = 50,kn = 60,hnn = 2)
integer,parameter::N = yn*hnn
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0)
complex::Ham(N,N) = 0
complex g1(hnn,hnn),g2(hnn,hnn),g3(hnn,hnn)
!=================================
real m0,tx,ty,lamx,lamy
!================cheevd===============
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork
integer lrwork
integer liwork
integer info
end module pub
!============================================================
program sol
use pub
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
!------------------------------------
m0 = 0.5
tx = 1.0
ty = -1.0
lamx = 1.0
lamy = 1.0
call main1()
stop
end program sol
!============================================================
subroutine main1()
use pub
integer m1
real k
open(3,file="openx-m1.dat")
open(4,file="openy-m1.dat")
do m1 = -kn,kn
k = pi*m1/kn
call openx(k)
write(3,999)k/pi,(w(i),i = 1,N)
call openy(k)
write(4,999)k/pi,(w(i),i = 1,N)
end do
close(3)
close(4)
999 format(201f11.6)
end subroutine main1
!============================================================
subroutine openx(ky)
use pub
real ky
call pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hnn
do l = 1,hnn
Ham(m,l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(m,l + hnn) = tx/2.0*g3(m,l) + lamx/(2*im)*g1(m,l)
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hnn
do l = 1,hnn
Ham(k*hnn + m,k*hnn + l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = tx/2.0*g3(m,l) - lamx/(2*im)*g1(m,l)
end do
end do
else
do m = 1,hnn
do l = 1,hnn ! k start from 1,matrix block from 2th row
Ham(k*hnn + m,k*hnn + l) = lamy*sin(ky)*g2(m,l) + (m0 + ty*cos(ky))*g3(m,l)
Ham(k*hnn + m,k*hnn + l + hnn) = tx/2.0*g3(m,l) + lamx/(2*im)*g1(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = tx/2.0*g3(m,l) - lamx/(2*im)*g1(m,l)
end do
end do
end if
end do
!------------------------
call isHermitian()
call eigsol()
return
end subroutine openx
!============================================================
subroutine openy(kx)
use pub
real kx
call pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hnn
do l = 1,hnn
Ham(m,l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(m,l + hnn) = lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hnn
do l = 1,hnn
Ham(k*hnn + m,k*hnn + l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = -lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
else
do m = 1,hnn
do l = 1,hnn ! k start from 1,matrix block from 2th row
Ham(k*hnn + m,k*hnn + l) = lamx*sin(kx)*g1(m,l) + (m0 + tx*cos(kx))*g3(m,l)
Ham(k*hnn + m,k*hnn + l + hnn) = lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = -lamy/(2*im)*g2(m,l) + ty/2.0*g3(m,l)
end do
end do
end if
end do
!------------------------
call isHermitian()
call eigsol()
return
end subroutine openy
!============================================================
subroutine pauli()
use pub
g1(1,hnn) = 1
g1(2,1) = 1
!-----------------
g2(1,hnn) = -im
g2(2,1) = im
!---------------
g3(1,1) = 1
g3(2,2) = -1
end subroutine pauli
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(16,file = 'hermitian.dat')
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
write(16,*)"===================="
write(*,*)"Ham isn't Hermitian"
stop
end if
end do
end do
close(16)
return
end subroutine isHermitian
!================= 矩阵本征值求解 ==============
subroutine eigSol()
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.dat",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine eigSol
Chern Number计算
陈数的计算公式在这里就不赘述了,模型也有了,直接上代码和结果,具体想看到底是怎么算Chern的,可以参考两种方法计算Chern Number这篇文章
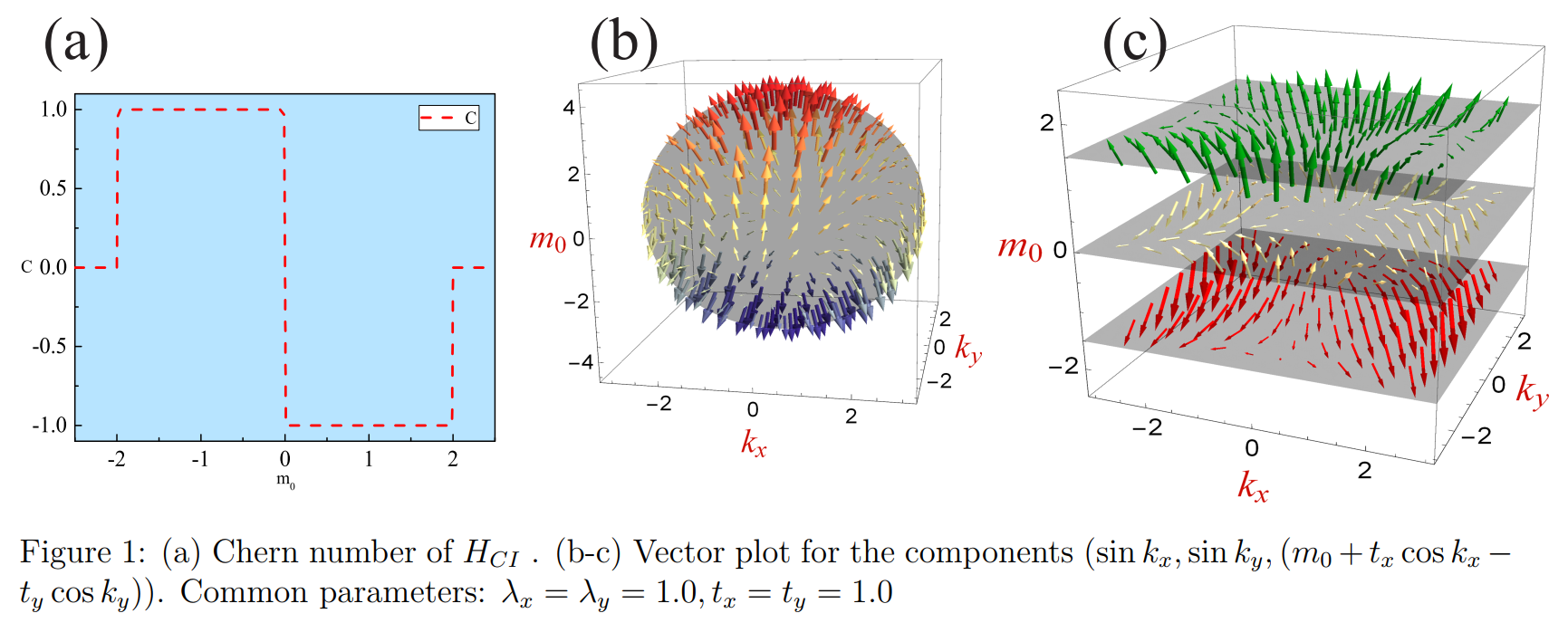
using LinearAlgebra,PyPlot,DelimitedFiles
# -----------------------------------------------------------------------
function matSet(kx::Float64,ky::Float64,m0::Float64)::Matrix{ComplexF64}
#m0::Float64 = 0.5
tx::Float64 = 1.0
ty::Float64 = -1.0
lamx::Float64 = 1.0
lamy::Float64 = 1.0
ham = zeros(ComplexF64,2,2)
ham[1,1] = (m0 + tx*cos(kx) + ty*cos(ky))
ham[2,2] = -(m0 + tx*cos(kx) + ty*cos(ky))
ham[1,2] = lamx*sin(kx) - 1im*lamy*sin(ky)
ham[2,1] = conj(ham[1,2])
return ham
end
#--------------------------------------------------------------------------
function ux(kx::Float64,ky::Float64,ne::Int64,m0::Float64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky,m0))[:,1]
#-----
wx = eigvecs(matSet(kx + del,ky,m0))[:,1]
#------
return w0'*wx/abs(w0'*wx)
end
#---------------------------------------------------------------------------
function uy(kx::Float64,ky::Float64,ne::Int64,m0::Float64)::ComplexF64
del::Float64 = pi/ne
#----
w0 = eigvecs(matSet(kx,ky,m0))[:,1]
#-----
wy = eigvecs(matSet(kx,ky + del,m0))[:,1]
#------
return w0'*wy/abs(w0'*wy)
end
#---------------------------------------------------------------------------
function img1(xlist::Array{Float64},ylist::Array{Float64},zlist::Array{ComplexF64})
zlist = map(imag,zlist)
#p1 = scatter(xlist,ylist,zlist*20,c=zlist*0.1,edgecolors="b",cmap="Reds")
p1 = scatter(xlist,ylist,zlist*200,c=zlist,cmap="Reds")
colorbar(p1)
xlabel("kx")
ylabel("ky")
title("Berry Curvature")
savefig("Berry Curature.png",bbox_inches="tight",dpi=60)
end
#----------------------------------------------------------------------------
function ChernNumber(m0::Float64)
ne::Int64 = 100
del::Float64 = pi/ne
kx::Float64 = 0.0
ky::Float64 = 0.0
flux::ComplexF64 = 0.0 + 0.0im
chern_num::ComplexF64 = 0.0 + 0.0im
kxlist = Float64[]
kylist = Float64[]
flist = ComplexF64[]
for m1 = -ne:ne
kx = m1*pi/ne
for m2 = -ne:ne
append!(kxlist,kx)
ky = m2*pi/ne
append!(kylist,ky)
flux = log((ux(kx,ky,ne,m0)*uy(kx + del,ky,ne,m0))/(ux(kx,ky + del,ne,m0)*uy(kx,ky,ne,m0)))
append!(flist,flux)
chern_num = chern_num + flux
end
end
#img1(kxlist,kylist,flist)
return round(real(chern_num/(2.0*pi*1im)))
end
#--------------------------------------------
function main1()
ch::Float64 = 0.0
chlist = []
plist = []
f1 = open("chern.dat","w")
for m0 in -2.5:0.01:2.5
ch = ChernNumber(m0)
append!(chlist,ch)
append!(plist,m0)
writedlm(f1,[m0 ch])
end
close(f1)
#plot(plist,chlist)
end
# =============================================
main1()
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |