准粒子(QPI)干涉计算
Fortran
1 | module pub |
把文章仔细读过之后,再利用那些公式写出上面Fortran的程序并不难,但是上面的计算中有一个问题,那就是所有的执行都是串行的,不管我的服务器有多厉害还,cpu利用率也就只是100%,所以计算速度比较慢,虽然Fortran也是可以并行的,但是之前在看的时候,发现如果想用Fortran并行,需要去学习一下mpi或者openmpi,而且还必须在服务器上安装好这个玩意才可以,想想就觉得这是一个大工程,不过自己又正好熟悉Julia,这个号称速度比肩Fortran,灵活性比肩python的编程这一点我是已经体验过了,速度上的优势还没体现出来,正好在这里借这个文章来利用Julia的多线程计算一下准粒子干涉,体现一下速度优势.
Julia
1 | using ProgressMeter |
总结
从速度上来说确实这里Julia的优势是很明显的,因为这里开了16个线程同时计算,在相同的参数下计算,Julia很快就可以计算完成,而Fortran的话,估计要算很久,因为是单线程串行,所以速度是相当的慢,而且这里在计算的时候因为嵌套的循环比较多,这就导致这种写法下,Fortran的计算速度真的就是很慢了,所以在这里Julia是获胜了.最重要的是,利用julia进行并行多线程的时候,并不需要很复杂的东西,只需要掌握简单的知识就好了,它用到的额外的几个库,用很简单的命令增加库就可以,相比较与Fortran来说简直就是态方便了.
Julia + Gnuplot
虽然Julia也可以绘图,但是使用起来始终没有Gnupltot那么方便,这里可以通过调整一下程序,让得到的数据结果可以方便的利用Gnuplot来绘图1
2
3
4
5
6
7
8
9
10
11
12
13
14file = "result"
form = ".dat"
filename = join([file,1,form])
f1 = open(filename,"w")
# code for plot
#PyPlot.set_cmap("gray_r")
#imsave(filename * ".png", -final)
for qx in 1:N
for qy in 1:N
writedlm(f1,[qx*pi/N qy*pi/N final[qx,qy]])
end
writedlm(f1," ")
end
close(f1)
经过这样的修改之后,首先filename = join([file,1,form])可以实现批量命名文件,只要修改其中的第二个参数就可以,在for循环中加入writedlm(f1," ")是为了让内层循环计算一次之后,数据之间加入一个空行,这是为了配合Gnuplot绘图.
gnuplot 密度图
绘图模板如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29set encoding iso_8859_1
set terminal postscript enhanced color
set output 'arc_r.eps'
set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1680
set output 'density.png'
set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
set palette defined ( -10 "blue", 0 "white", 10 "red" )
set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
set size ratio -1
set view map
set xtics
set ytics
set xlabel "K_1 (1/{\305})"
set xlabel "k_x"
set ylabel "K_2 (1/{\305})"
set ylabel "k_y"
set ylabel offset 1, 0
set colorbox
set xrange [0:1]
set yrange [0:1]
set pm3d interpolate 4,4
splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'result1.dat' u 1:2:3 w pm3d
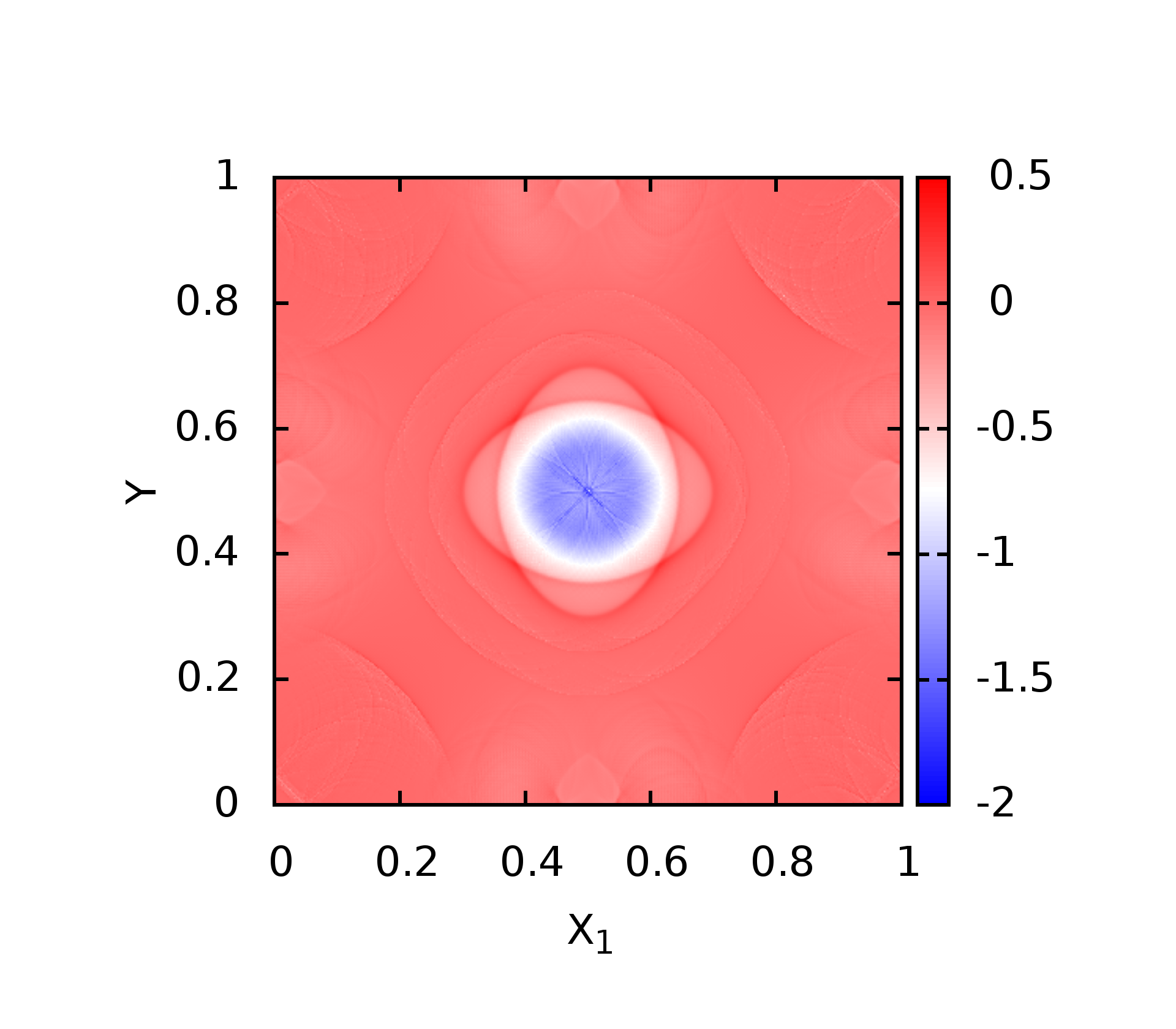
鉴于该网站分享的大都是学习笔记,作者水平有限,若发现有问题可以发邮件给我
- yxliphy@gmail.com
也非常欢迎喜欢分享的小伙伴投稿






![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

