这里我想继续通过WannierTools来计算实例中的Weyl半金属这个模型,因为这个实例是直接通过哈密顿量来进行研究的,所以将这个例子学习清楚,之后遇到哈密顿量,可以直接通过这种方式来计算其对应的一些拓扑性质,极大的方便研究.
Weyl Semimetal
这个实例中,$\mathbf{\Gamma}$点的哈密顿量为 \(H=A(k_x\sigma_x+k_y\sigma_y)+\left[M_0-M_1(k_x^2+k_y^2+k_z^2) \right]\) 参数$A=M_0=M_1=1$
这个博客中学习的实例同样来自于源代码中examples文件夹中
这个哈密顿量的紧束缚模型的数据可以通过实例中的writeHmnR.f90这个文件产生,得到的数据如下
Tight Binding 数据解析
在这里主要来研究一下如何通过一个具体的哈密顿量来产生紧束缚的数据,首先系统的哈密顿量为
\(H=A(k_x\sigma_x+k_y\sigma_y)+\left[M_0-M_1(k_x^2+k_y^2+k_z^2)\sigma_z \right]\)
参数$A=M_0=M_1=1$.在将连续模型变为离散的格点模型的时候,需要进行$\cos(x)\rightarrow 1 - \frac{1}{2}x^2,\sin(x)\rightarrow x$的替换,所以上面的连续模型在变成紧束缚模型之后为
\(H(\mathbf{k})=A(\sin(k_x)\sigma_x+\sin(k_y)\sigma_y)+\left[M_0-6M_1+2M_1(\cos(k_x)+\cos(k_y)+\cos(k_z))\sigma_z \right]\)
将这个紧束缚近似模型改写到实空间中的Wannier轨道上,也就是做下面的变换
\(\sin(k)=\frac{1}{2i}(e^{ik}-e^{-ik})\\
\cos(k)=\frac{1}{2}(e^{ik}+e^{-ik})\\
c_i=\frac{1}{\sqrt{\mathcal{N}}}\sum_{k}e^{-ik}c_k\)
能看懂紧束缚近似模型,肯定就清楚如何从sin,cos变成离散的格点形式,所以这里直接了当的认为$e^{ik_x}$就是就是电子在$x$正方向上的hopping,那么相应的$e^{-ik_x}$则是代表电子在$x$负方向上的hopping.
下面再来对泡里矩阵$\sigma$进行分析理解,因为这里讨论的是一个2轨道模型,也就是一个2带模型,所以$\sigma_x$相关的项就表示轨道间(带间)耦合是简并的,而对于$\sigma_y$则轨道间(带间)的耦合是相反的,最后对于$\sigma_z$这一项,是不存在轨道间(带间)耦合的.所以对于$\cos(k_x)\sigma_z$,它代表着轨道1自己于自己在$x$正方向上的hopping大小是$M_1$,而在$x$负方向上hopping的大小也是$M_1$.其余各项的分析和这个都是相同的,至于$M_0$与单独的$M_1$项,则是代表了on-site的能量,也就是没有hopping.
下面来将上面所说的内容用公式来表达,首先记 $\mathbf{R}=x\mathbf{R_x} + y\mathbf{R_y} + z\mathbf{R_z}\rightarrow (x,y,z)$,这里 $\mathbf{R_i}$ 代表 $i$ 方向上的基矢,我在这里就以最简单的四方点阵来研究,若向$x$正方向hopping,对于$2M_1\cos(k_x)\sigma_z$可以写作
\(\textrm{(x,y,z)}\quad\textrm{band1}\quad\textrm{band2}\quad\textrm{hopping_Re}\quad\textrm{hopping_Im}\\
(1,0,0)\quad 1\quad 1\quad M_1\quad 0\\
(1,0,0)\quad 2\quad 2\quad -M_1\quad 0\)
这里前三个数代表的是hopping方向的基矢,因为是向$x$正方向hopping,所以$x=1,y=0,z=0$,而$M_1\cos(k_x)\sigma_z$这一项代表的只有轨道内的hopping,没有轨道间的hopping,所以这里第2和第3列只存在$1\quad 1,2\quad 2$,但是不同轨道内hopping的大小是相反的,所以第四列分别对应着一正一负的值,而且从这里看出这一项的hopping值都是实数,所以最后一列代表的hopping的虚部就都为0. 这里就是如何将紧束缚哈密顿量中的一项完全转换成Wannier轨道之间波函数overlap的过程.
下面是由Fortran利用这个紧束缚模型产生的数据,我们首先要搞明白它输出的数据的结构,下面就是数据结构,先来说明一下每一行每一列分别代表的意义
2-band 3D WSM toy model # 第一行是注释,一般用来说明数据的相关信息
2 # 第二行是轨道的数量
7 # 第三行是hopping元胞的数量,we call it NRPTS
1 1 1 1 1 1 1 # 由于这个紧束缚的数据是自己手动产生的,而不是由Wannier90得到,所以 There are NRPTS number of 1.
0 0 0 1 1 -5.00000000 0.00000000 # 下面的就是由上面分析紧束缚哈密顿量在对应的hopping方向上的具体信息
0 0 0 1 2 0.00000000 0.00000000
0 0 0 2 1 0.00000000 0.00000000
0 0 0 2 2 5.00000000 0.00000000
1 0 0 1 1 1.00000000 0.00000000
1 0 0 1 2 0.00000000 0.50000000
1 0 0 2 1 0.00000000 0.50000000
1 0 0 2 2 -1.00000000 0.00000000
-1 0 0 1 1 1.00000000 0.00000000
-1 0 0 1 2 -0.00000000 -0.50000000
-1 0 0 2 1 -0.00000000 -0.50000000
-1 0 0 2 2 -1.00000000 0.00000000
0 1 0 1 1 1.00000000 0.00000000
0 1 0 1 2 0.50000000 0.00000000
0 1 0 2 1 -0.50000000 0.00000000
0 1 0 2 2 -1.00000000 0.00000000
0 -1 0 1 1 1.00000000 0.00000000
0 -1 0 1 2 -0.50000000 0.00000000
0 -1 0 2 1 0.50000000 0.00000000
0 -1 0 2 2 -1.00000000 0.00000000
0 0 1 1 1 1.00000000 0.00000000
0 0 1 1 2 0.00000000 0.00000000
0 0 1 2 1 0.00000000 0.00000000
0 0 1 2 2 -1.00000000 0.00000000
0 0 -1 1 1 1.00000000 0.00000000
0 0 -1 1 2 0.00000000 0.00000000
0 0 -1 2 1 0.00000000 0.00000000
0 0 -1 2 2 -1.00000000 0.00000000
! 2-band 3D WSM model
! usage:
! compile and run
! gfortran writeHmnR.f90 -o writehmnr
! ./writehmnr
! > H=A(kx*s_x+ky*s_y)+(M0-M1(kx*kx+ky*ky+kz*kz))*s_z
program writeHmnR
implicit none
integer, parameter :: dp=kind(1d0) !计算精度设置
complex(dp), parameter :: zi= (0d0, 1d0) ! 虚数i
complex(dp), parameter :: zzero= (0d0, 0d0) ! 复数0
integer :: i, j
integer :: ir
integer :: nwann
!> arrays for hamiltonian storage
integer :: nrpts
integer, allocatable :: ndegen(:) ! 定义未定大小的数组,后面会给这些数组分配空间
integer, allocatable :: irvec(:, :)
complex(dp), allocatable :: hmnr(:, :, :)
!> three lattice constants
real(dp) :: A, M0, M1
A = 1d0
M0 = 1d0
M1 = 1d0
nwann = 1
nrpts = 17
! 给数组分配空间,确定数组的大小
allocate(irvec(3, nrpts))
allocate(ndegen(nrpts))
allocate(hmnr(nwann*2, nwann*2, nrpts))
irvec = 0
ndegen = 1 ! 因为我们实在通过一个紧束缚哈密顿量手动产生tight binding的数据,所以在数据的第四行需要对所有的hopping元胞位置都设置成1,这是程序的要求,也就正如上面数据格式中的第四行所示,这个数组就是用来做这件事情的
hmnr = zzero ! 矩阵初始化
! 在所有hopping方向上设置hopping的大小
! 0 0 0
ir = 1
irvec(1, ir) = 0
irvec(2, ir) = 0
irvec(3, ir) = 0
hmnr(1, 1, ir) = M0 - 6d0*M1
hmnr(2, 2, ir) = -M0 + 6d0*M1
!1 0 0
ir = ir + 1 ! ir = 2
irvec(1, ir) = 1
irvec(2, ir) = 0
irvec(3, ir) = 0
hmnr(1, 1, ir) = M1
hmnr(1, 2, ir) = zi*A/2d0
hmnr(2, 1, ir) = zi*A/2d0
hmnr(2, 2, ir) = -M1
!-1 0 0
ir = ir + 1 ! ir = 3
irvec(1, ir) = -1
irvec(2, ir) = 0
irvec(3, ir) = 0
hmnr(1, 1, ir) = M1
hmnr(1, 2, ir) = -zi*A/2d0
hmnr(2, 1, ir) = -zi*A/2d0
hmnr(2, 2, ir) = -M1
! 0 1 0
ir = ir + 1 ! ir = 4
irvec(1, ir) = 0
irvec(2, ir) = 1
irvec(3, ir) = 0
hmnr(1, 1, ir) = M1
hmnr(1, 2, ir) = A/2d0
hmnr(2, 1, ir) = -A/2d0
hmnr(2, 2, ir) = -M1
!0 -1 0
ir = ir + 1 ! ir = 5
irvec(1, ir) = 0
irvec(2, ir) = -1
irvec(3, ir) = 0
hmnr(1, 1, ir) = M1
hmnr(1, 2, ir) = -A/2d0
hmnr(2, 1, ir) = A/2d0
hmnr(2, 2, ir) = -M1
! 0 0 1
ir = ir + 1 ! ir = 6
irvec(1, ir) = 0
irvec(2, ir) = 0
irvec(3, ir) = 1
hmnr(1, 1, ir) = M1
hmnr(2, 2, ir) = -M1
! 0 0 -1
ir = ir + 1 ! ir = 7
irvec(1, ir) = 0
irvec(2, ir) = 0
irvec(3, ir) = -1
hmnr(1, 1, ir) = M1
hmnr(2, 2, ir) = -M1
nrpts = ir
!> write to new_hr.dat 写出数据
open(unit=105, file='Weyl3D_hr.dat')
write(105, *)'2-band 3D WSM toy model'
write(105, *)nwann*2
write(105, *)nrpts
write(105, '(15I5)')(ndegen(i), i=1, nrpts) ! 这里是写入手动产生tight binding所需要的1
do ir = 1, nrpts
do i = 1, nwann*2
do j = 1, nwann*2
write(105, '(5I5, 2f16.8)')irvec(:, ir), i, j, HmnR(i, j, ir)
end do
end do
end do
close(105)
stop
end ! end of program
接下来就是准备控制计算的wt.in文件,然后执行计算
cp wt.in-bands wt.in # 计算体态能带
wt.x & # 开始计算
gnuplot bulkek.gnu # 画体态能带图
继续来学习wt.in这个控制文件中的一些参数,首先来看计算体态能带的控制文件
&TB_FILE
Hrfile = "Weyl3D_hr.dat" ! 紧束缚能带数据
/
!> bulk band structure calculation flag
&CONTROL
BulkBand_calc = T ! 计算体态能带
/
&SYSTEM
NumOccupied = 1 ! NumOccupied 占据态数目
SOC = 1 ! SOC=1代表此时考虑自旋轨道耦合
E_FERMI = 0 ! e-fermi 费米能大小
/
&PARAMETERS
Nk1 = 60 ! number k points(作图时k点的数目)
/
LATTICE ! 元胞基矢,与VASP中的结构相同
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors(元胞中只有一个原子)
Direct ! Direct or Cartisen coordinate(这个原子的空间坐标,此时是采用直接坐标的方式,还有一种分数坐标的表示方法)
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details 表面基矢方向确定,在计算表面态时的控制参数
0 0 1
1 0 0
0 1 0
KPATH_BULK ! k point path 计算体态能带时的路径控制,通常这个路径都是选取BZ中的高对称路径
2 ! number of k line only for bulk band
X 0.50000 0.00000 0.0000 G 0.00000 0.00000 0.0000
G 0.00000 0.00000 0.0000 Z 0.00000 0.00000 0.5000
最终结果如下
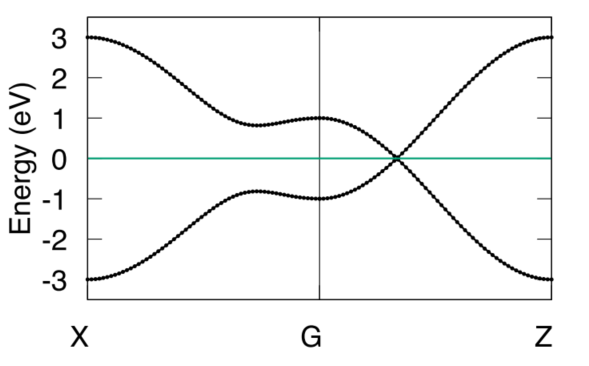
Weyl Point
Weyl半金属的体态能带中存在Weyl点,接下来就通过计算来寻找这些简并点
cp wt.in-findnodes wt.in
wt.x &
gnuplot Nodes.gnu
继续分析参数控制文件wt.in
&TB_FILE
Hrfile = "Weyl3D_hr.dat"
/
!> bulk band structure calculation flag
&CONTROL
FindNodes_calc = T ! 这个参数的控制是个逻辑变量,T代表寻找Weyl点
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi
/
&PARAMETERS
Nk1 = 6 ! number k points 这个值变大,会使得计算时间变长,不过计算结果更好
Nk2 = 6 ! number k points
Nk3 = 6 ! number k points
Gap_threshold = 0.0001 ! threshold for GapCube output 计算Weyl点总需要设置一个范围值,不然真的就是个点
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details
0 0 1
1 0 0
0 1 0
KCUBE_BULK
0.00 0.00 0.00 ! Original point for 3D k plane 基矢的初始点位置选取
1.00 0.00 0.00 ! The first vector to define 3d k space plane 三个基矢方向
0.00 1.00 0.00 ! The second vector to define 3d k space plane
0.00 0.00 1.00 ! The third vector to define 3d k cube
计算结束之后,会生成一个Nodes.dat的文件,里面就是Weyl点的位置信息,绘图结果如下
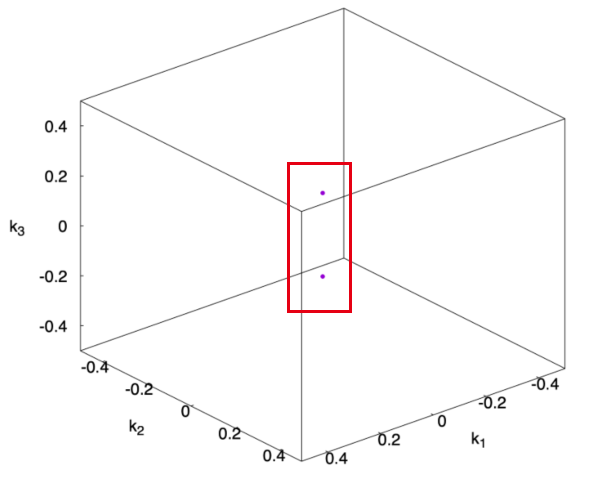
Chirality of Weyl points
每个Weyl点的手性是不同的,这里接着来计算一下上面寻找到的Weyl点对应的手性
cp wt.in-chirality wt.in
wt.x &
gnuplot wanniercenter3D_Weyl_1.gnu
gnuplot wanniercenter3D_Weyl_2.gnu
分析参数控制文件wt.in
&TB_FILE
Hrfile = "Weyl3D_hr.dat"
/
!> bulk band structure calculation flag
&CONTROL
WeylChirality_calc = T ! 计算不同Weyl点的手性
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi
/
&PARAMETERS
Nk1 = 60 ! number k points
Nk2 = 60 ! number k points
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details
0 0 1
1 0 0
0 1 0
WEYL_CHIRALITY
2 ! Num_Weyls Weyl点的数目
Cartesian ! Direct or Cartesian coordinate
0.004 ! Radius of the ball surround a Weyl point 相当于是一个化学势填充,使得Weyl点变成一个小球
0.00000000 -0.00000000 1.04719755 ! 两个Weyl点的空间位置
0.00000000 0.00000000 -1.04719755
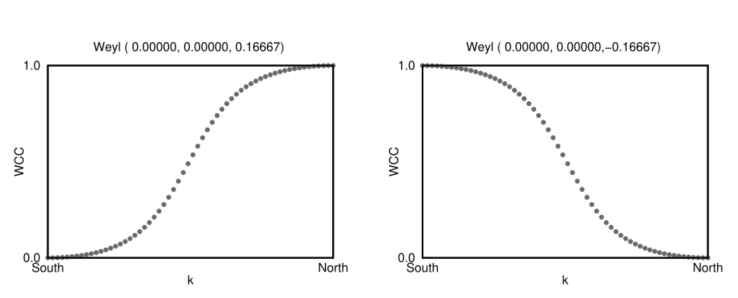
可以看到,咋不同的Weyl点周围,Wannier Center的绕行方向是相反的,也就说明这两个Weyl点的手性是相反的.这个计算的手性同样可以从输出文件WT.out中获取
sed -n '/Chiralities/,/Time/p' WT.out
Calculate Berry curvature
因为Weyl半金属是三维的,所以再计算Berry曲率的时候,可以选择多个不同的平面来计算,这个面的选取有KPLANE_BULK这个参数来控制,我们这里选取$k_y=0$这个平面,来计算$(k_x,k_z)$面上的Berry曲率,设置如下
KPLANE_BULK Direct
0.00 0.00 0.00 ! Center of 3D k slice
1.00 0.00 0.00 ! The first vector along x direction
0.00 0.00 1.00 ! The second vector along z direction
开始计算
cp wt.in-Berry-curvature wt.in
wt.x &
gnuplot Berrycurvature-normalized.gnu-tutorial # 结果绘制
分析控制文件
&TB_FILE
Hrfile = "Weyl3D_hr.dat"
/
!> bulk band structure calculation flag
&CONTROL
BerryCurvature_calc = T ! 计算Berry曲率的开关
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi
/
&PARAMETERS
Nk1 = 60 ! number k points
Nk2 = 60 ! number k points
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details
0 0 1
1 0 0
0 1 0
KPLANE_BULK ! 因为Berry曲率是个2D的,Weyl体系是3D的,这里就是控制要计算的是哪个平面上的Berry曲率
Direct
0.00 0.00 0.00 ! Center for 3D k slice
1.00 0.00 0.00 ! The first vector is along x direction
0.00 0.00 1.00 ! The second vector is along z direction
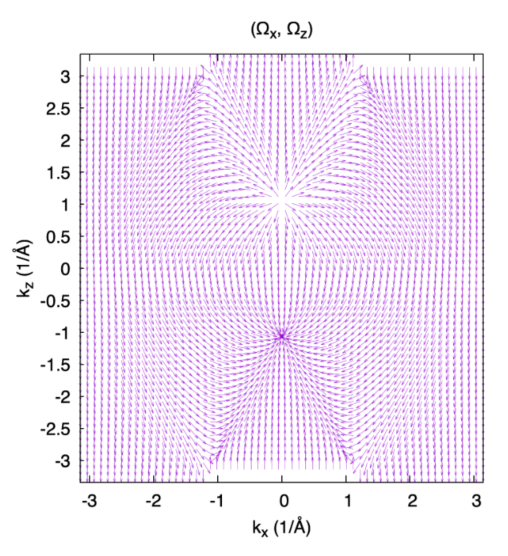
丛结果上来看,再Weyl点上,Berry曲率是有奇异的,一个是Berry曲率的源,另外一个是汇.
表面态计算
Weyl半金属一个很重要的特征就是存在表面的费米弧连接着体态的Weyl点,由上面的计算可知两个Weyl点实在$k_z$轴上,所以选择$k_y$这个方向是开边界的,$(k_x,k_z)$是周期的,来计算一下表面态,这里主要就是要通过设置SURFACE这个参数来选择要计算哪个方向上的表面态.
SURFACE !计算(0,1,0)表面上的表面态,所以这里设置了(kx,kz)方向都是周期的
1 0 0
0 0 1
开始计算
cp wt.in-surfacestates wt.in
wt.x &
gnuplot surfdos_l.gnu
gnuplot arc_l.gnu
分析计算控制文件wt.in
&TB_FILE
Hrfile = "Weyl3D_hr.dat"
/
!> bulk band structure calculation flag
&CONTROL
SlabSS_calc = T ! 计算表面态
SlabArc_calc = T ! 计算Fermi弧
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi 费米能量的位置
/
&PARAMETERS
Eta_Arc = 0.001 ! infinite small value, like brodening
E_arc = 0.0 ! energy for calculate Fermi Arc 计算费米弧的能量位置
OmegaNum = 400 ! omega number 这个值跟表面态的计算是相关的,值越大计算细节越清晰
OmegaMin = -1.6 ! energy interval 控制表面态能量计算的区间
OmegaMax = 1.6 ! energy interval
Nk1 = 201 ! number k points
Nk2 = 201 ! number k points
NP = 2 ! number of principle layers(我理解这个是开边界方向的格点数目)
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details
1 0 0 ! 这里只是设置了x和z方向的矢量,表明这两个方向是周期的,所以计算的是(010)表面上的表面态
0 0 1
KPATH_SLAB ! 控制slab结构下计算表面态的路径
1 ! numker of k line for 2D case
-X -0.50 0.0 X 0.5 0.0 ! k path for 2D case
KPLANE_SLAB
-0.5 -0.5 ! Original point for 2D k plane
1.0 0.0 ! The first vector to define 2D k plane
0.0 1.0 ! The second vector to define 2D k plane for arc plots
计算结果如下
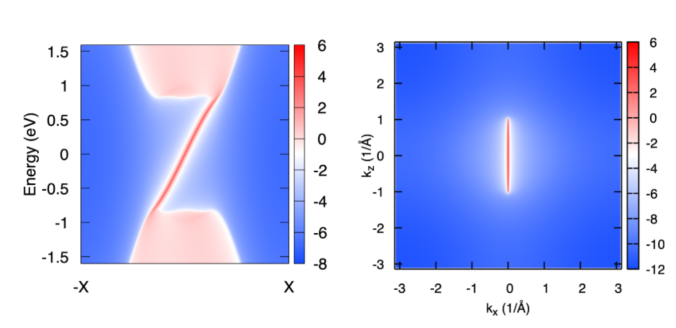
可以从计算结果清楚的看到存在边界态和表面上的费米弧(Fermi arc).
Wannier Charge Center(WCC)
体系的拓扑性质同样可以从WCC的演化来判断,费米弧(Fermi arc)也仅仅只是存在于两个Weyl点之间,这一点同样可以从WCC的演化中判断.
cp wt.in-wcc-kz0 wt.in
wt.x &
gnuplot wcc.gnu
cp wcc.eps wcc-kz0.eps
cp wt.in-wcc-kz0.5 wt.in
wt.x &
gnuplot wcc.gnu
cp wcc.eps wcc-kz0.5.eps
分析计算控制文件wt.in
&TB_FILE
Hrfile = "Weyl3D_hr.dat" ! 紧束缚模型数据
/
!> bulk band structure calculation flag
&CONTROL
Wanniercenter_calc = T ! 计算Wannier Center演化
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi
/
&PARAMETERS
Nk1 = 60 ! number k points
Nk2 = 60 ! number k points
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details 控制表面方向
0 0 1
1 0 0
0 1 0
KPLANE_BULK
Direct
0.00 0.00 0.00 ! Original point for 3D k plane
0.00 1.00 0.00 ! The second vector to define 3d k space plane
1.00 0.00 0.00 ! The first vector to define 3d k space plane
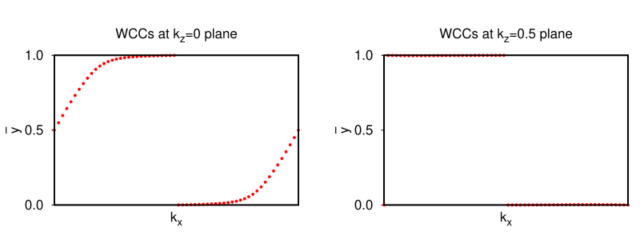
从这个结果中可以看到,如果计算的平面截过Fermi arc,那么Chern number就是1,否则就是0.其实本质上Chern number就是Wannier Charge Center(WCC)再参数变化一个周期时候的winding.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |