自己研究生期间的工作是在一个PRL的基础上进行的,那篇文章中的有效边界理论是个很好用的工具,文章作者严忠波老师将研究过程写的非常仔细,也给了我一个很好的学习机会,这里将文章中用到的有效边界理论进行一个仔细的推导
{:.info}

微分方程通解

因为涉及到求解微分方程,这里先预热一下,回顾如何求解一个2阶线性齐次微分方程

$\begin{equation} my(x)+\frac{t}{2}y''(x)+\lambda y'(x)=0\qquad\textrm{with}\qquad y(0)=y(+\infty)=0 \end{equation}$

eigenroot equation is expressed as

$\begin{eqnarray} &\frac{t}{2}r^2+\lambda r+m=0\\ &r_{1,2}=-\frac{\lambda}{t}\pm\sqrt{\frac{\lambda^2}{t^2}-\frac{2m}{t}}=\alpha\pm i\beta \end{eqnarray}$

where $\alpha = -\frac{\lambda}{t}$, $\beta=\sqrt{\frac{2m}{t}-\frac{\lambda^2}{t^2}}$, in here we suppose $\frac{\lambda^2}{t^2}-\frac{2m}{t}<0$, general solution is

$\begin{equation} y(x)=e^{\alpha x}(C_1\cos \beta x+C_2\sin \beta x) \end{equation}$

with boundary condition $y(0)=y(\infty)=0$ we have

$\begin{equation} y(x)=\mathcal{N}\sin(\beta x)e^{-\alpha x} \end{equation}$ $\begin{equation} my(x)+\frac{t}{2}y''(x)-\lambda y'(x)=0\qquad\textrm{with}\qquad y(0)=y(-\infty)=0 \end{equation}$

eigenroot equation is expressed as

$\begin{eqnarray} &\frac{t}{2}r^2-\lambda r+m=0\\ &r_{1,2}=\frac{\lambda}{t}\pm\sqrt{\frac{\lambda^2}{t^2}-\frac{2m}{t}}=\alpha\pm i\beta \end{eqnarray}$

where $\alpha=\frac{\lambda}{t}$, $\beta=\sqrt{\frac{2m}{t}-\frac{\lambda^2}{t^2}}$, general solution is

$\begin{equation} y(x)=e^{\alpha x}(C_1\cos \beta x+C_2\sin \beta x) \end{equation}$

with boundary condition $y(0)=y(-\infty)=0$ we have

$\begin{equation} y(x)=\mathcal{N}\sin(\beta x)e^{\alpha x} \end{equation}$

BHZ模型边界态

$\begin{equation} H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y \end{equation}$

by expanding around $\mathbf{\Gamma}=(0,0)$

$\begin{equation} H(\mathbf{k})=(m_0+\frac{t_x}{2}k_x^2+\frac{t_y}{2}k_y^2)\sigma_z+\lambda_xk_x\sigma_xs_z+\lambda_yk_y\sigma_y \end{equation}$

replace $k_x\rightarrow -i\partial_x$ and decompose the Hamiltonian as $H=H_0+H_p$, in which

$\begin{equation} \begin{aligned} H_0(-i\partial_x,k_y)&=(m-t_x\partial_x^2/2)\sigma_z-i\lambda_x\sigma_xs_z\partial_x\\ H_p(-i\partial_x,k_y)&=\lambda_yk_y\sigma_y \end{aligned} \end{equation}$

For edge $1$

solving the eigenvalue equation $H_0\psi_\alpha(x)=E_\alpha\psi_\alpha$ under the boundary condition $\psi_\alpha(0)=\psi_\alpha(+\infty)=0$

$\begin{equation} \begin{aligned} &(m-t_x\partial_x^2/2+\lambda_x\partial_x)\phi(x)=0\\ &(\sigma_z-i\sigma_xs_z)\xi_\alpha=0 \end{aligned} \end{equation}$

we find two zero-energy solutions, whose froms are

$\begin{equation} \psi_\alpha(x)=\phi(x)\xi_\alpha=\mathcal{N}_x\sin(\kappa_1x)e^{\kappa_2x}e^{ik_yy}\xi_\alpha \end{equation}$

with normalization given by

$\begin{equation}|\mathcal{N}_x|^2=4|\kappa_2(\kappa_1^2+\kappa_2^2)/\kappa_1^2|\qquad \kappa_1=\sqrt{|(2m_0/t_x)|-(\lambda_x^2/t_x^2)}\qquad\kappa_2=-\frac{\lambda_x}{t_x}\end{equation}$

The eigenvectors $\xi_\alpha$ satisfy $\sigma_ys_z\xi_\alpha=-\xi_\alpha$. We explicitly choose them as

$\begin{equation} \begin{aligned} \xi_1&=|\sigma_y=-1\rangle\otimes|\uparrow\rangle\\ \xi_2&=|\sigma_y=+1\rangle\otimes|\downarrow\rangle\\ \end{aligned} \end{equation}$

The matrix elements of the perturbation $H_p$ in this basis are

$\begin{equation} H_{1,\alpha\beta}=\int_{0}^{+\infty}dx\psi^*_\alpha(x)H_p(-i\partial_x,k_y)\psi_\beta(x) \end{equation}$

We use $H_p(-i\partial_x,k_y)=\lambda_yk_y\sigma_y$ and $\sigma_ys_z\xi_\alpha=-\xi_\alpha$, the final form of the effective Hamiltonian is

$\begin{equation} H_{1}(k_y)=-\lambda_yk_ys_z \end{equation}$

For edge $3$

solving the eigenvalue equation $H_0\psi_\alpha(x)=E_\alpha\psi_\alpha$ under the boundary condition $\psi_\alpha(0)=\psi_\alpha(-\infty)=0$

$\begin{equation} \begin{aligned} &(m-t_x\partial_x^2/2-\lambda_x\partial_x)\phi(x)=0\\ &(\sigma_z+i\sigma_xs_z)\xi_\alpha=0 \end{aligned} \end{equation}$

we find two zero-energy solutions, whose froms are

$\begin{equation} \psi_\alpha(x)=\phi(x)\xi_\alpha=\mathcal{N}_x\sin(\kappa_1x)e^{\kappa_2x}e^{ik_yy}\xi_\alpha \end{equation}$

with normalization given by

$\begin{equation}|\mathcal{N}_x|^2=4|\kappa_2(\kappa_1^2+\kappa_2^2)/\kappa_1^2|\qquad\kappa_1=\sqrt{|(2m_0/t_x)|-(\lambda_x^2/t_x^2)}\qquad\kappa_2=\frac{\lambda_x}{t_x}\end{equation}$

The eigenvectors $\xi_\alpha$ satisfy $\sigma_ys_z\xi_\alpha=\xi_\alpha$. We explicitly choose them as

$\begin{equation} \begin{aligned} \xi_1&=|\sigma_y=-1\rangle\otimes|\downarrow\rangle\\ \xi_2&=|\sigma_y=+1\rangle\otimes|\uparrow\rangle\\ \end{aligned} \end{equation}$

The matrix elements of the perturbation $H_p$ in this basis are

$\begin{equation} H_{3,\alpha\beta}=\int_{-\infty}^{0}dx\psi^*_\alpha(x)H_p(-i\partial_x,k_y)\psi_\beta(x) \end{equation}$

We use $H_p(-i\partial_x,k_y)=\lambda_yk_y\sigma_y$ and $\sigma_ys_z\xi_\alpha=\xi_\alpha$, the final form of the effective Hamiltonian is

$\begin{equation} H_{3}(k_y)=\lambda_yk_ys_z \end{equation}$

replace $k_y\rightarrow -i\partial_y$ and decompose the Hamiltonian as $H=H_0+H_p$, in which

$\begin{equation} \begin{aligned} H_0(-i\partial_y,k_x)&=(m-t_y\partial_y^2/2)\sigma_z-i\lambda_y\sigma_y\partial_y\\ H_p(-i\partial_y,k_x)&=\lambda_xk_x\sigma_xs_z \end{aligned} \end{equation}$

For edge $2$

solving the eigenvalue equation $H_0\psi_\alpha(x)=E_\alpha\psi_\alpha$ under the boundary condition $\psi_\alpha(0)=\psi_\alpha(+\infty)=0$

$\begin{equation} \begin{aligned} &(m-t_y\partial_y^2/2+\lambda_y\partial_y)\phi(y)=0\\ &(\sigma_z-i\sigma_y)\xi_\alpha=0 \end{aligned} \end{equation}$

we find two zero-energy solutions, whose froms are

$\begin{equation} \psi_\alpha(y)=\phi(y)\xi_\alpha=\mathcal{N}_y\sin(\kappa_1y)e^{\kappa_2y}e^{ik_xx}\xi_\alpha \end{equation}$

with normalization given by

$\begin{equation}|\mathcal{N}_y|^2=4|\kappa_2(\kappa_1^2+\kappa_2^2)/\kappa_1^2|\qquad\kappa_1=\sqrt{|(2m_0/t_y)|-(\lambda_y^2/t_y^2)}\qquad\kappa_2=-\frac{\lambda_y}{t_y}\end{equation}$

The eigenvectors $\xi_\alpha$ satisfy $\sigma_x\xi_\alpha=\xi_\alpha$. We explicitly choose them as

$\begin{equation} \begin{aligned} \xi_1&=|\sigma_x=-1\rangle\otimes|\downarrow\rangle\\ \xi_2&=|\sigma_x=+1\rangle\otimes|\uparrow\rangle\\ \end{aligned} \end{equation}$

The matrix elements of the perturbation $H_p$ in this basis are

$\begin{equation} H_{2,\alpha\beta}=\int_{0}^{+\infty}dy\psi^*_\alpha(y)H_p(-i\partial_y,k_x)\psi_\beta(y) \end{equation}$

We use $H_p(-i\partial_x,k_y)=\lambda_xk_x\sigma_xs_z$ and $\sigma_x\xi_\alpha=\xi_\alpha$, the final form of the effective Hamiltonian is

$\begin{equation} H_{2}(k_y)=\lambda_xk_xs_z \end{equation}$

For edge $4$

solving the eigenvalue equation $H_0\psi_\alpha(x)=E_\alpha\psi_\alpha$ under the boundary condition $\psi_\alpha(0)=\psi_\alpha(-\infty)=0$

$\begin{equation} \begin{aligned} &(m-t_y\partial_y^2/2-\lambda_y\partial_y)\phi(y)=0\\ &(\sigma_z+i\sigma_y)\xi_\alpha=0 \end{aligned} \end{equation}$ $\begin{equation} \psi_\alpha(y)=\phi(y)\xi_\alpha=\mathcal{N}_y\sin(\kappa_1y)e^{\kappa_2y}e^{ik_xx}\xi_\alpha \end{equation}$

with normalization given by

$\begin{equation}|\mathcal{N}_y|^2=4|\kappa_2(\kappa_1^2+\kappa_2^2)/\kappa_1^2|\qquad\kappa_1=\sqrt{|(2m_0/t_y)|-(\lambda_y^2/t_y^2)}\qquad\kappa_2=\frac{\lambda_y}{t_y}\end{equation}$

The eigenvectors $\xi_\alpha$ satisfy $\sigma_x\xi_\alpha=-\xi_\alpha$. We explicitly choose them as

$\begin{equation} \begin{aligned} \xi_1&=|\sigma_x=-1\rangle\otimes|\uparrow\rangle\\ \xi_2&=|\sigma_x=+1\rangle\otimes|\downarrow\rangle\\ \end{aligned} \end{equation}$

The matrix elements of the perturbation $H_p$ in this basis are

$\begin{equation} H_{4,\alpha\beta}=\int_{-\infty}^{0}dy\psi^*_\alpha(y)H_p(-i\partial_y,k_x)\psi_\beta(y) \end{equation}$

We use $H_p(-i\partial_x,k_y)=\lambda_xk_x\sigma_xs_z$ and $\sigma_x\xi_\alpha=-\xi_\alpha$, the final form of the effective Hamiltonian is

$\begin{equation} H_{4}(k_y)=-\lambda_xk_xs_z \end{equation}$

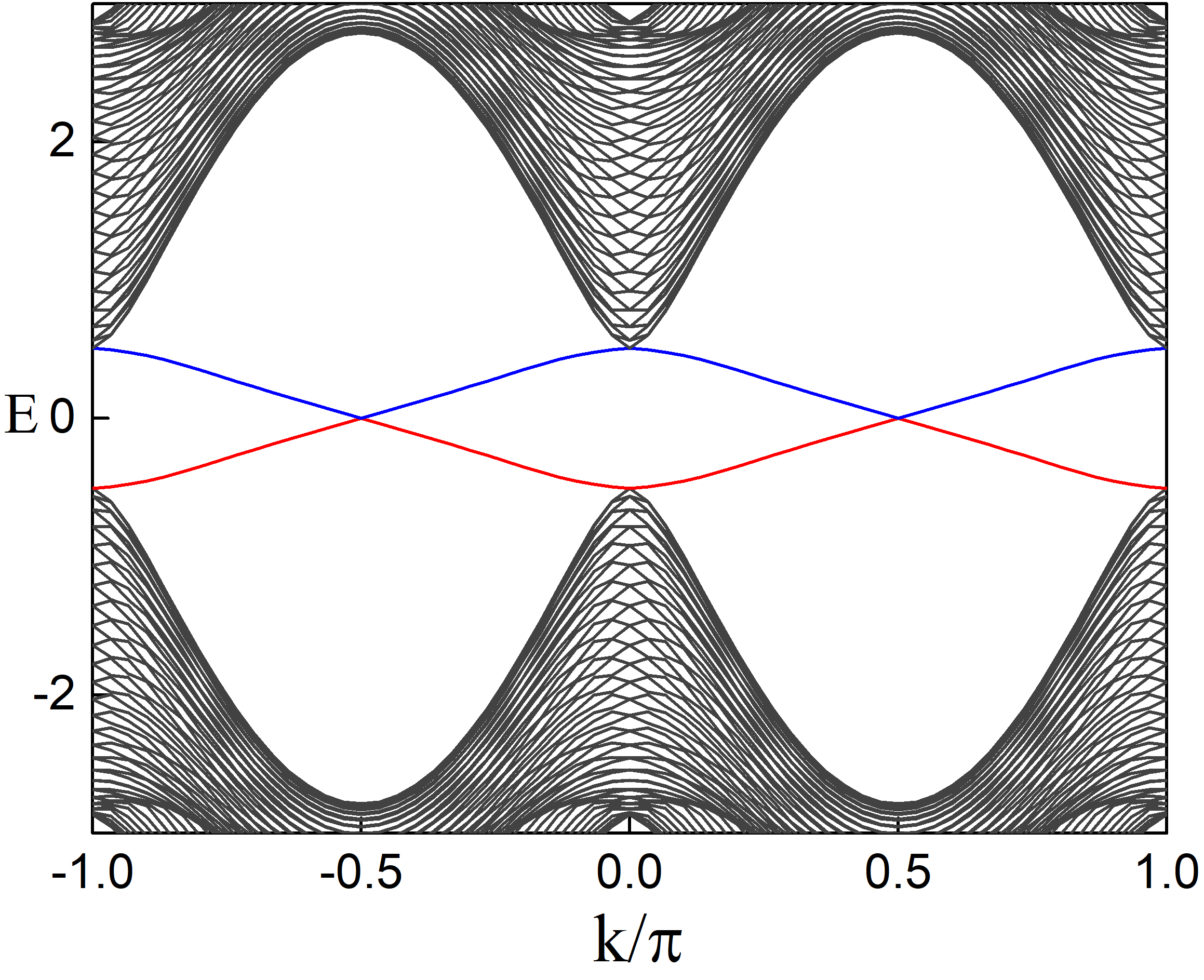
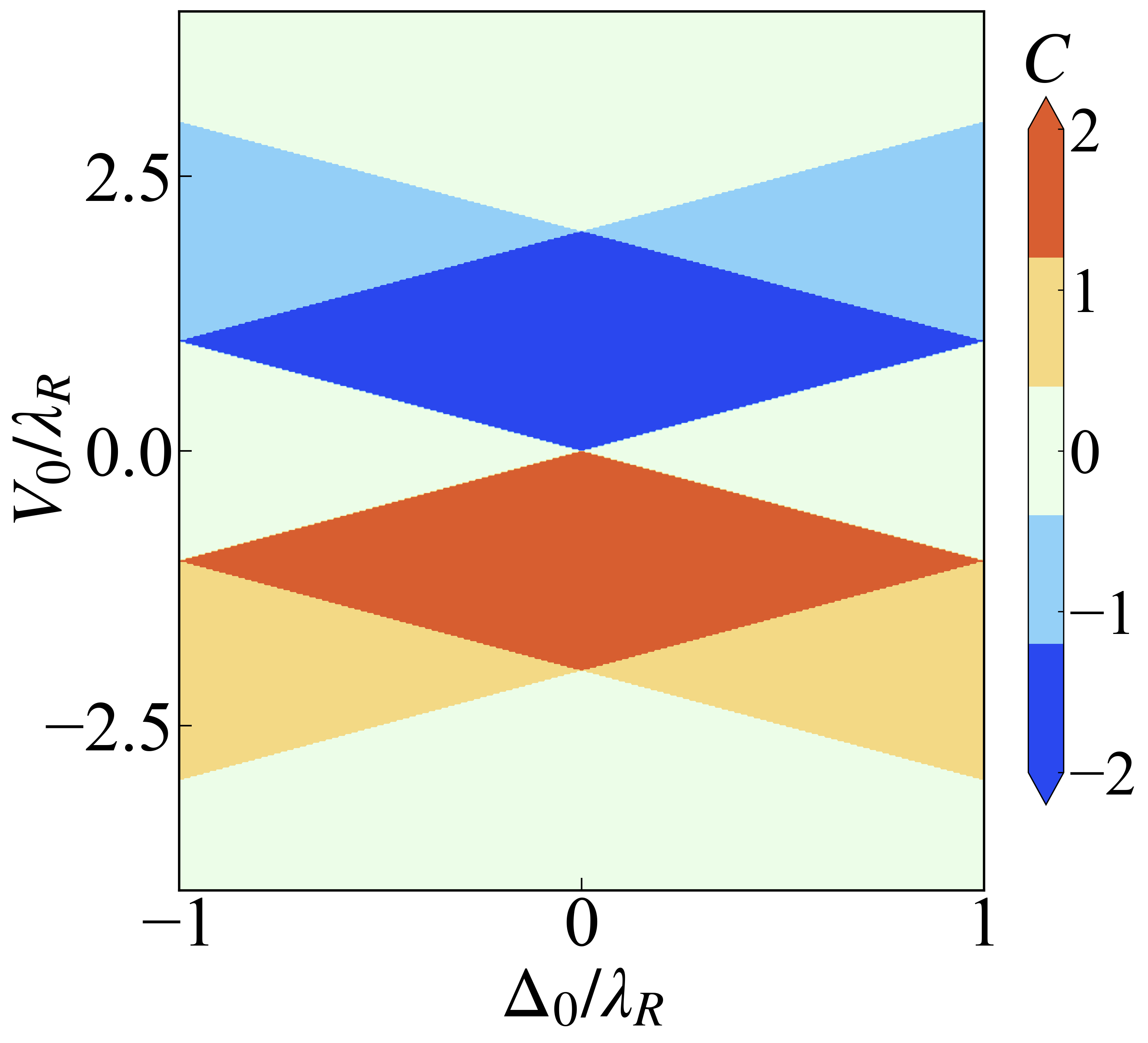
Therefore, the final form of the effective Hamiltonian for the four edges are

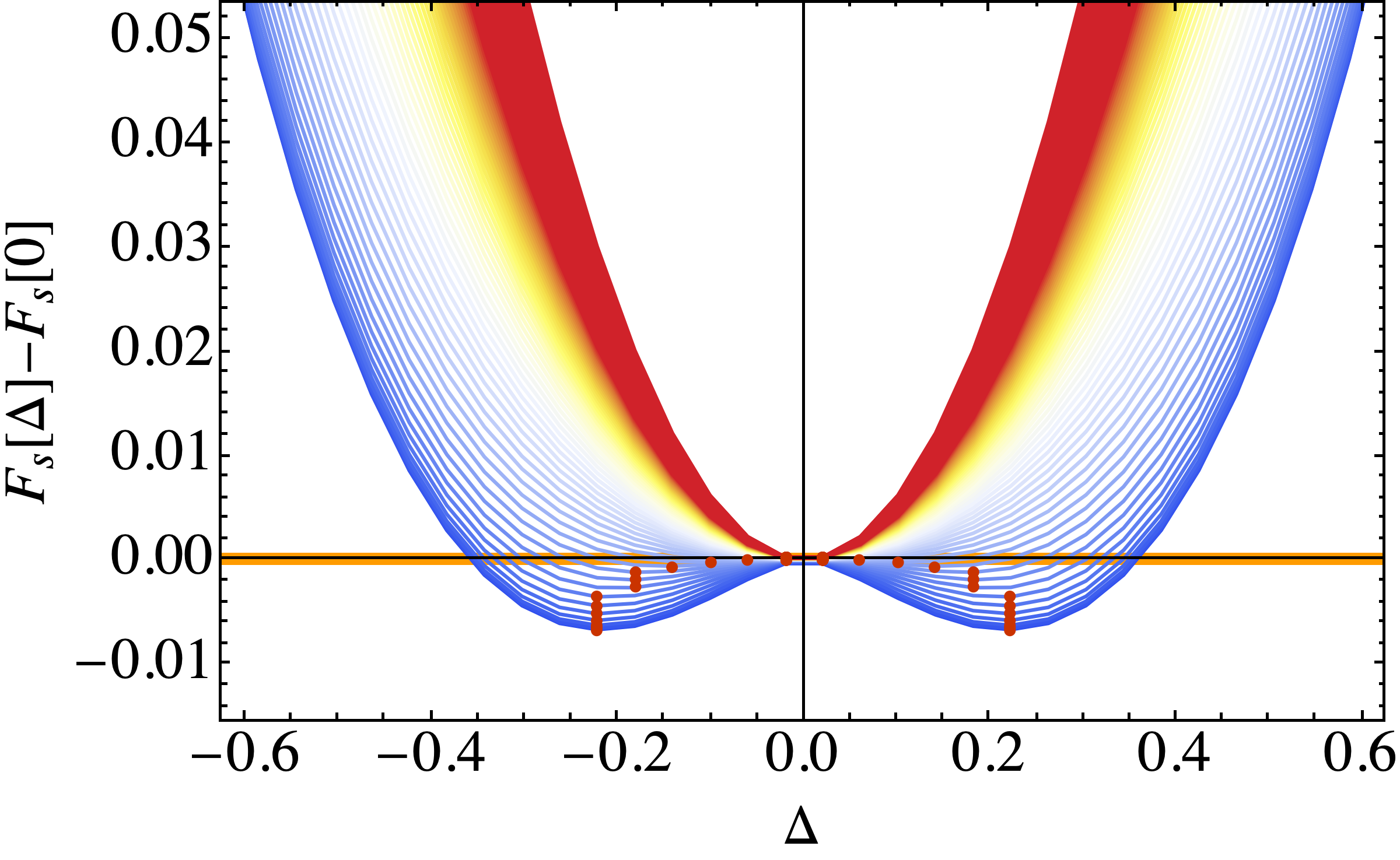
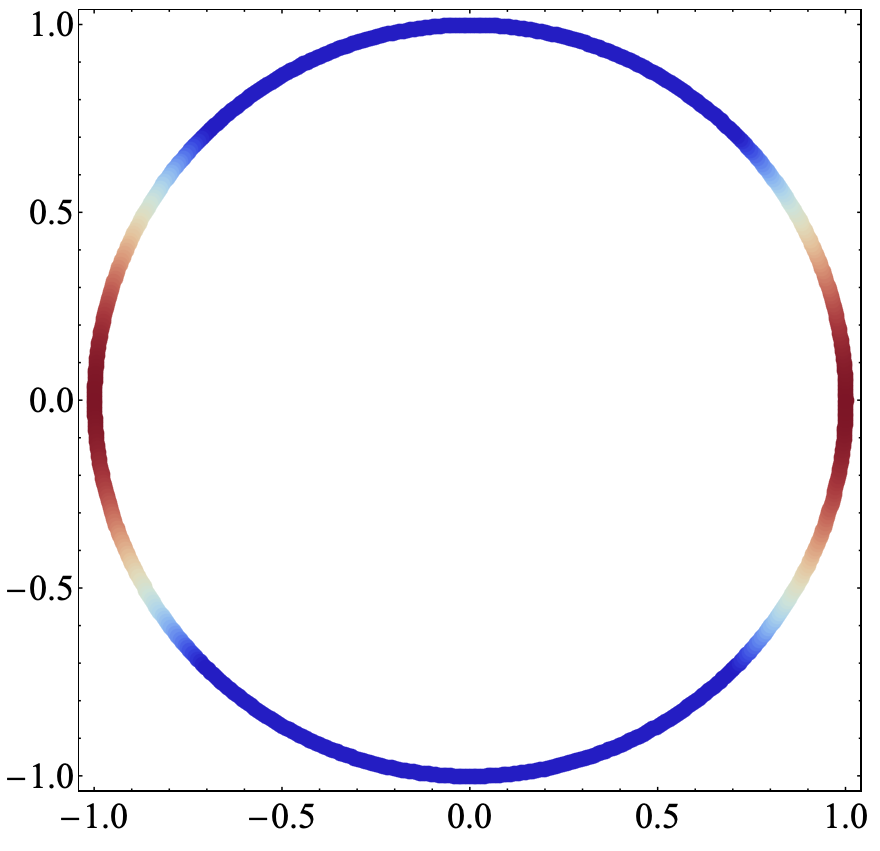
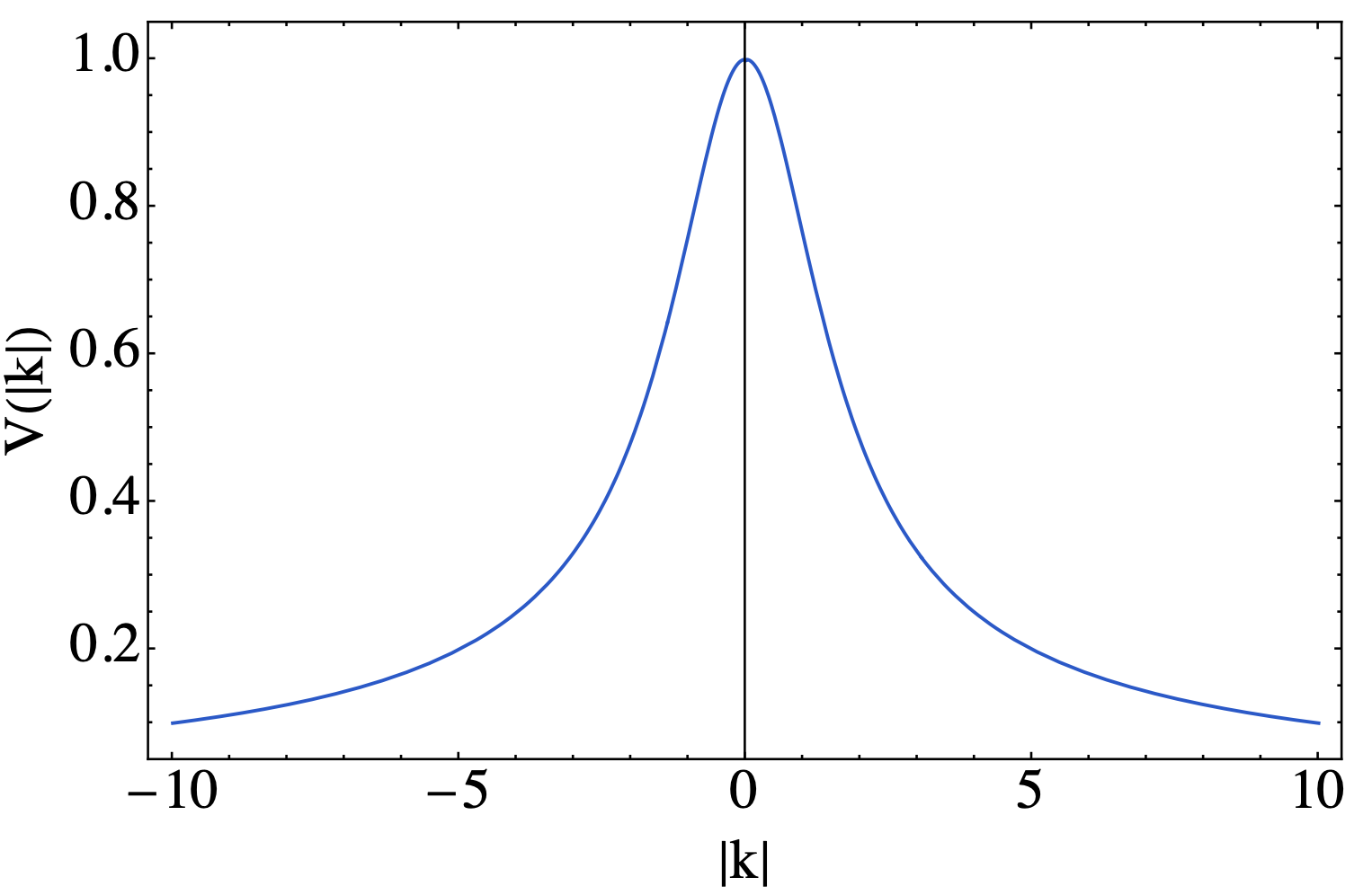
Results

$\begin{equation} \begin{aligned} H_{1}(k_y)&=-\lambda_yk_ys_z\\ H_{2}(k_x)&=\lambda_xk_xs_z\\ H_{3}(k_y)&=\lambda_yk_ys_z\\ H_{4}(k_x)&=-\lambda_xk_xs_z\\ \end{aligned} \end{equation}$