在有效边界这篇博客中,主要是求解了关于边界理论的微分方程,对于边界态波函数的spinor部分也只是利用Pauli矩阵的对易关系得到了spinor需要满足的本征方程,这里就来推导一下spinor部分到底如何计算,以及如何根据spinor部分来选择计算微扰时候的基矢.
{:.info}

这里以文章Majorana Corner Modes in a High-Temperature Platform为基础,来重复其中spinor部分的计算和基矢的选取.

边界态计算

$\begin{equation} H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z\tau_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y\tau_z+\Delta(\mathbf{k})s_y\tau_y \end{equation}$

by expanding around $\mathbf{\Gamma}=(0,0)$

$\begin{equation} H(\mathbf{k})=(m_0+\frac{t_x}{2}k_x^2+\frac{t_y}{2}k_y^2)\sigma_z\tau_z+\lambda_xk_x\sigma_xs_z+\lambda_yk_y\sigma_y\tau_z-\frac{1}{2}(\Delta_xk_x^2+\Delta_yk_y^2)s_y\tau_y \end{equation}$

replace $k_x\rightarrow -i\partial_x$ and decompose the Hamiltonian as $H=H_0+H_p$, in which

$\begin{equation} \begin{aligned} H_0(-i\partial_x,k_y)&=(m-t_x\partial_x^2/2)\sigma_z\tau_z-i\lambda_x\sigma_xs_z\partial_x\\ H_p(-i\partial_x,k_y)&=\lambda_yk_y\sigma_y\tau_z+\frac{1}{2}\Delta_xs_y\tau_y\partial_x^2 \end{aligned} \end{equation}$

基矢构造

solving the eigenvalue equation $H_0\psi_\alpha(x)=E_\alpha\psi_\alpha$ under the boundary condition $\psi_\alpha(0)=\psi_\alpha(+\infty)=0$

$\begin{equation} \begin{aligned} &(m-t_x\partial_x^2/2+\lambda_x\partial_x)\phi(x)=0\\ &(\sigma_z\tau_z-i\sigma_xs_z)\xi_\alpha=0 \end{aligned} \end{equation}$

we find two zero-energy solutions, whose froms are

$\begin{equation} \psi_\alpha(x)=\phi(x)\xi_\alpha=\mathcal{N}_x\sin(\kappa_1x)e^{\kappa_2x}e^{ik_yy}\xi_\alpha \end{equation}$

with normalization given by

$\rvert \mathcal{N}_x\rvert ^2=4\rvert \kappa_2(\kappa_1^2+\kappa_2^2)/\kappa_1^2\rvert\\ \kappa_1=\sqrt{\rvert (2m_0/t_x)\rvert -(\lambda_x^2/t_x^2)}, \kappa_2=-\frac{\lambda_x}{t_x}$

The eigenvectors $\xi_\alpha$ satisfy $\sigma_ys_z\xi_\alpha=-\xi_\alpha$. We explicitly choose them as

$\begin{equation} \begin{aligned} \xi_1&=\rvert \sigma_y=-1\rangle\otimes\rvert \uparrow\rangle\\ \xi_2&=\rvert \sigma_y=+1\rangle\otimes\rvert \downarrow\rangle\\ \end{aligned} \end{equation}$

The matrix elements of the perturbation $H_p$ in this basis are

$\begin{equation} H_{1,\alpha\beta}=\int_{0}^{+\infty}dx\psi^*_\alpha(x)H_p(-i\partial_x,k_y)\psi_\beta(x) \end{equation}$

We use $H_p(-i\partial_x,k_y)=\lambda_yk_y\sigma_y$ and $\sigma_ys_z\tau_z\xi_\alpha=-\xi_\alpha$,

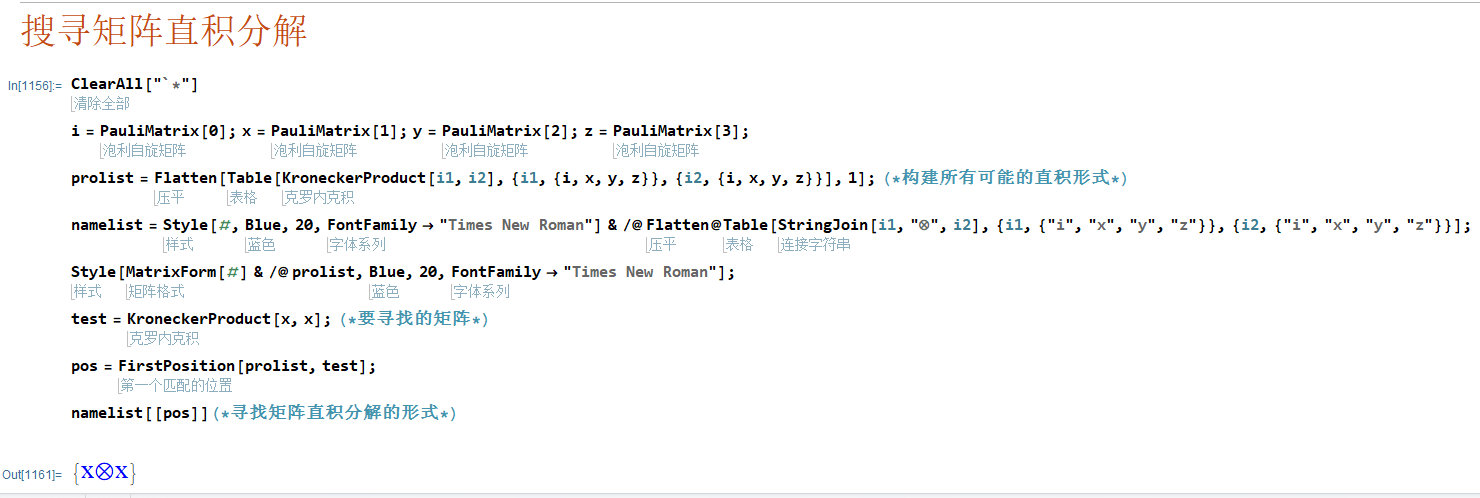
这里可以清晰的看到$\xi_\alpha$是$\sigma_ys_z\tau_z$的本征态,那么可以求解矩阵$\sigma_y\otimes s_z\otimes\tau_z$的本征值与本征矢量,这里可以知道,只需要求解本征值为-1的本征矢量即可,这个过程利用Mathematica进行,这样可以之后将程序拓展为其他情形

png

这里就可以求解得到$\sigma_y\otimes s_z\otimes\tau_z$矩阵的8个本征值和本征矢量,其中只需要本征值为-1的本征矢量,这样就相当于寻找到了$\xi_\alpha$. 这里可以看到矩阵是由三个代表不同自由度的Pauli矩阵直积而成,那么自然可以联想是否可以使用每个自由度的Pauli矩阵对应的本征矢量来构建这个直积矩阵$\Gamma_1=\sigma_y\otimes s_z\otimes\tau_z$满足$\sigma_ys_z\tau_z\xi_\alpha=-\xi_\alpha$的本征矢量$\xi_\alpha$?

答案是可行的,首先知道要求解的是$\Gamma_1$本征值为$-1$的本征矢量$\xi_\alpha$,那么在通过小的Pauli矩阵构造时,要满足三个不同自由度$s,\sigma,\tau$对应的本征值相乘之后应该是$-1$,则对应的三个本征矢量直积之后就可以得到$\xi_\alpha$,这个过程仍然利用Mathematica进行计算

png

这里程序的基本思路是:(1)首先遍历三个Pauli矩阵所有对应的本征值与本征矢量,然后进行直积组合,因为Pauli矩阵的本征值只有$\{+1,-1\}$两种情况,所以所有的组合中,对应的本征值也只有$\{+1,-1\}$,组合得到的本征矢量共有8个,但根据$\Gamma_1$的要求,这里也只是选取组合本征值为$-1$的基矢,通过这样的一个流程之后,就可以知道$\Gamma_1$本征值为$-1$的基矢如何由$s,\sigma,\tau$构造的,也就是程序结果中蓝色所表示的结果.
{:.warning}

矩阵直积搜寻

通常在边界理论分析的时候,需要将几个矩阵分解成Pauli矩阵的直积形式(加入这个矩阵本来就是由Pauli矩阵直积而成的),比如文章中要求解

$H_{1,\alpha\beta}(k_y)=\int_{0}^{\infty}dx\psi^*_\alpha(x)H_p(-i\partial_x,k_y)\psi_\beta$

这其中就要涉及到求解

$M_1=\frac{1}{2}\Delta_x\int_0^\infty dx\psi^*_\alpha(\sigma_0s_y\tau_y)\partial_x^2\psi_\beta$

这个质量项,其中涉及到矩阵$\sigma_0s_y\tau_y$与spinor部分$\xi_\alpha$的运算

$\xi_\alpha^\dagger(\sigma_0s_y\tau_y)\xi_\beta=\Gamma_2$

根据前面的过程,我们已经可以求出$\xi_\alpha$的具体表达式

$\begin{equation} \begin{aligned} \xi_1&=|\sigma_y=-1\rangle\otimes|\uparrow\rangle\otimes|\tau_z=+1\rangle\\ \xi_2&=|\sigma_y=+1\rangle\otimes|\downarrow\rangle\otimes|\tau_z=+1\rangle\\ \xi_3&=|\sigma_y=-1\rangle\otimes|\uparrow\rangle\otimes|\tau_z=-1\rangle\\ \xi_4&=|\sigma_y=-1\rangle\otimes|\downarrow\rangle\otimes|\tau_z=-1\rangle\\ \end{aligned} \end{equation}$

那么根据$\xi_\alpha$就可以计算处$\Gamma_2$,但是如何把$\Gamma_2$写成Pauli矩阵的直积形式呢?如果对Pauli矩阵比较熟悉,自然可以看出来,但这里既然都是程序在计算,干脆也提供一下程序计算矩阵直积分解为Pauli矩阵的方法

png