这里是利用边界格林函数方法来计算边界态,相比于通常取cylinder的方法,计算速度上是要快一些,做出来的图可以更加清晰的反映边界态的特征.

在之前的Hamiltonian构建时的基矢选择这篇博客中,虽然是和哈密顿量基矢选择有关的问题,但是我同样展示了如何通过一个紧束缚哈密顿量来计算拓扑边界态,虽然这个方法也很常见,用的也比较多,但是有时候为了反映一些局部的特征,可能需要把开边界的格点数目取的非常大,这就会使的计算量变得很大,耗时较长,这里就想利用边界格林函数的方法来计算边界态,它的优点是此时需要的矩阵维度是很小的,主要就是进行迭代计算,如果所需要的精度合适,计算速度上的提升是非常客观的,而且可以将边界态的某些细节反映的非常好,这里就整理一下如何利用边界格林函数来计算这样的边界态.

模型方法

这里选用BHZ模型

$H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y\label{ham}$

计算方法如下,已经知道了$H$之后,系统的格林函数可以写作

$G^{-1}(z)=z-H=\left(\begin{array}{cccc} z-H_0&C&0&0\\ C^\dagger&z-H_0&C&0\\ 0&C^\dagger&z-H_0&C\\ 0&0&C^\dagger&\cdots \end{array}\right)\label{gf}$

where the diagonal block H0 describes the Hamiltonian within the same “principal layer,”这一项其实就是哈密顿量(\ref{ham})沿某一方向开边界之后,包含好量子数$k_i$的那部分,自然$C,C^\dagger$就是相邻格点之间的hopping项了,从这里就可以看出,这样哈密顿量需要处理的就只是很小的一块,计算量自然很小.

我们可以发现由于(\ref{gf})是个三对角形式,所以可以将它通过迭代的方式进行求解

$g^{(N)}_{ij}=(z-H_0-Cg^{(N-1)}C^\dagger)^{-1}_{ij}$

对于初始条件

$g^{(0)}=(z-H_0)^{-1}$

他就是系统的边界格林函数,当选择一定的迭代精度之后,就可以求解得到最后的边界格林函数$g^{(N)}$,通过格林函数就可以计算对应的谱函数,也就可以得到边界态的结果

$A(\omega,k_i)=-\frac{1}{\pi}\textrm{Im}(g^{(N)}(\omega,k_i))$

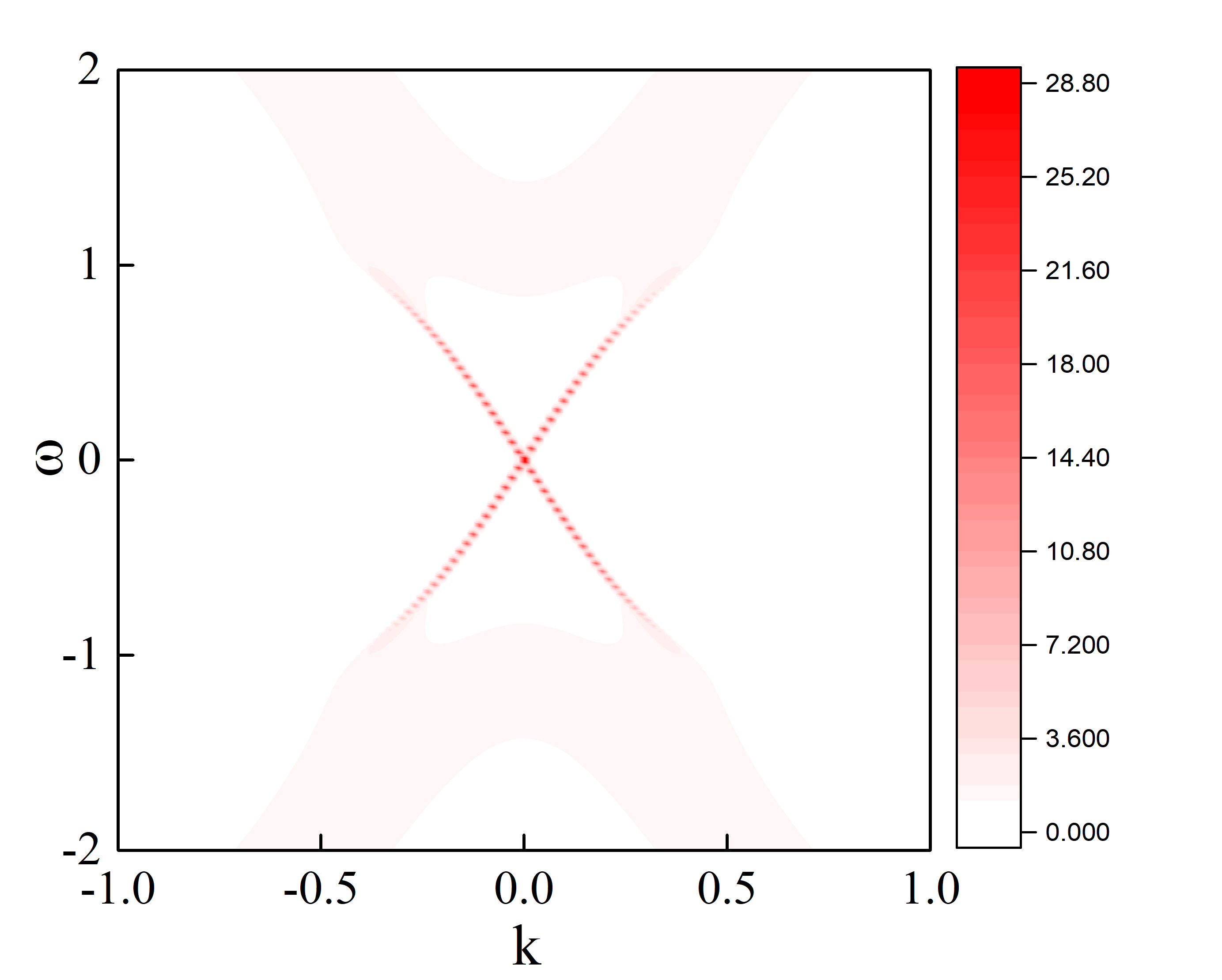
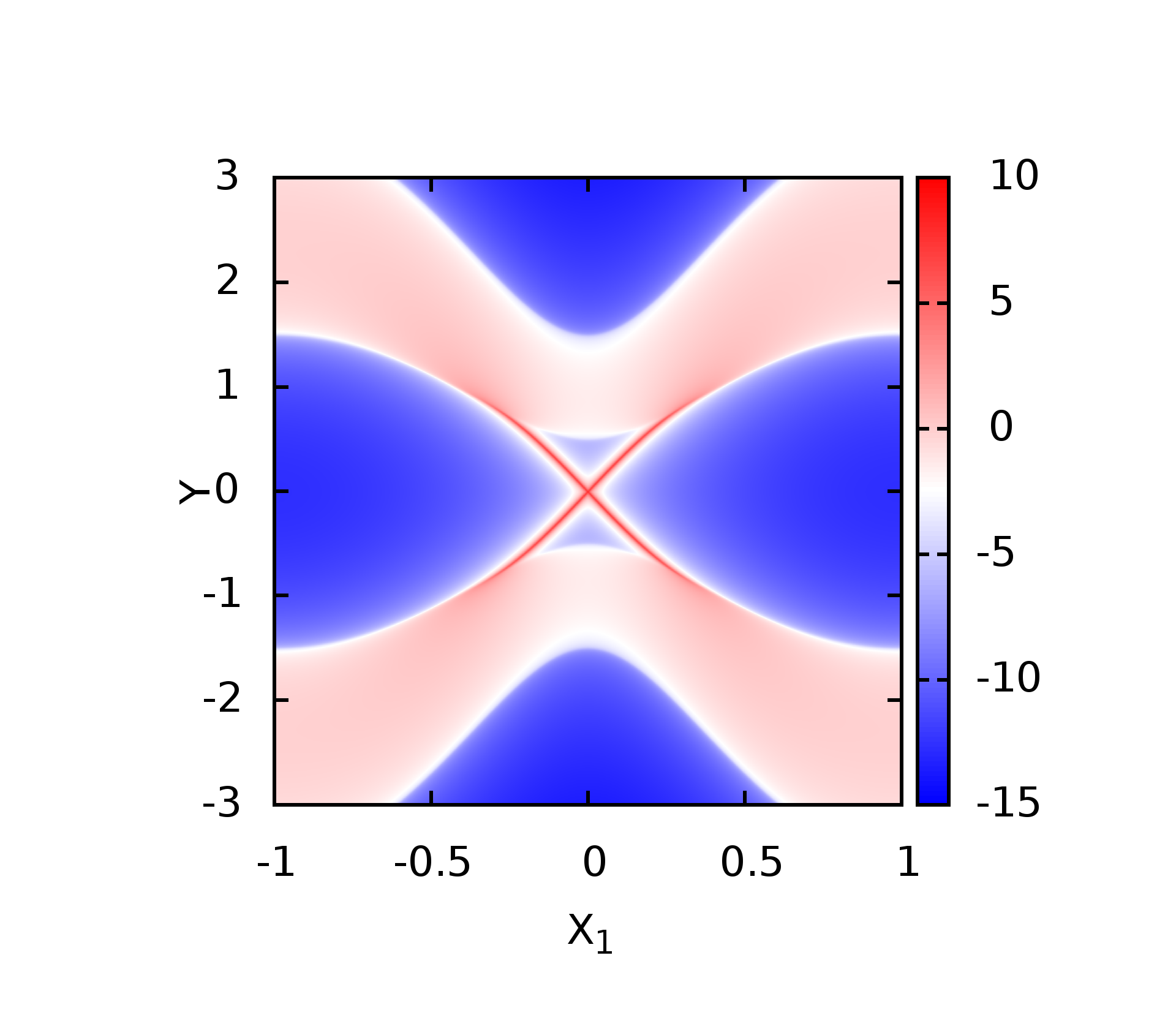
结果如下图

png

这里计算得到的图像并不是很光滑,这与计算的时候选择的计算间隔以及格林函数中的小虚部有关,而且和作图工具也有关系,不过我最近在学习利用gunplot来做图,因为是命令作图,基矢数据量非常大也不同担心电脑死机,而用类似origin的前端作图工具,当想让曲线光滑的时候,所需要的数据文件就会非常大,从而对电脑要求就会非常高,所以可以通过这些方面的改进来将这个图做得更好看.
{:.warning}

代码

Julia

using LinearAlgebra,DelimitedFiles,PyPlot
#---------------------------------------------------
function Pauli()
    hn = 4
    g1 = zeros(ComplexF64,hn,hn)
    g2 = zeros(ComplexF64,hn,hn)
    g3 = zeros(ComplexF64,hn,hn)
    #------ Kinetic energy
    g1[1,1] = 1
    g1[2,2] = -1
    g1[3,3] = 1
    g1[4,4] = -1
    #-------- SOC-x
    g2[1,2] = 1
    g2[2,1] = 1
    g2[3,4] = -1
    g2[4,3] = -1
    #---------- SOC-y
    g3[1,2] = -1im
    g3[2,1] = 1im
    g3[3,4] = -1im
    g3[4,3] = 1im
    return g1,g2,g3
end 
# ========================================================
function matset(ky::Float64)
    hn::Int64 = 4
    H00 = zeros(ComplexF64,4,4)
    H01 = zeros(ComplexF64,4,4)
    g1 = zeros(ComplexF64,4,4)
    g2 = zeros(ComplexF64,4,4)
    g3 = zeros(ComplexF64,4,4)
    #--------------------
    m0::Float64 = 1.5
    tx::Float64 = -1.0
    ty::Float64 = 1.0
    ax::Float64 = 1.0
    ay::Float64 = 1.0
    g1,g2,g3 = Pauli()
    #--------------------
    for m in 1:hn
        for l in 1:hn
            H00[m,l] = (m0-ty*cos(ky))*g1[m,l] + ay*sin(ky)*g3[m,l] 

            H01[m,l] = (-tx*g1[m,l] - 1im*ax*g2[m,l])/2
        end 
    end 
    #------
    return H00,H01
end
# =====================================================
function iteration(omg::Number,ky::Float64)
    hn::Int64 = 4
    eps::Float64 = 1e-8
    err::Float64 = 1.0
    num::Int64 = 0.0
    g0 = zeros(ComplexF64,hn,hn)
    giter = zeros(ComplexF64,hn,hn)
    gdiff = zeros(ComplexF64,hn,hn)
    unit = zeros(ComplexF64,hn,hn)
    h00 = zeros(ComplexF64,hn,hn)
    h01 = zeros(ComplexF64,hn,hn)
    h00,h01 = matset(ky)
    for i in 1:hn
        unit[i,i] = 1
    end
    g0 = inv(omg*unit - h00)
    while(err > eps)
        num += 1
        giter = inv(omg*unit - h00 - h01*g0*transpose(conj(h01))) 
        gdiff = giter - g0
        g0 = giter
        err = abs(sum(gdiff))
    end
    return g0
end
# ===========================================================
function main()
    hn::Int64 = 4
    g0 = zeros(ComplexF64,hn,hn)
    re::ComplexF64 = 0.0
    eta::Float64 = 0.01
    domg::Float64 = 0.01
    dk::Float64 = 0.01
    f1 = open("edgeState.dat","w")
    for omg in -2:domg:2
        for kx in -pi:dk:pi
            g0 = iteration(omg + 1im*eta,kx)
            re = -sum(g0)/pi
            writedlm(f1,[kx/pi omg imag(re)])
        end
    end
    close(f1)
end
# =============================================================
main()