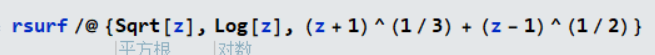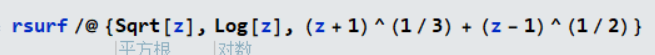在研究非厄米问题的时候总是会遇到复平面的问题,此时就需要用到黎曼面的知识,这篇博客整理了如何利用Mathematica绘制黎曼面.
{:.info}

外部程序绘制

png

png

png

png

png

png

png

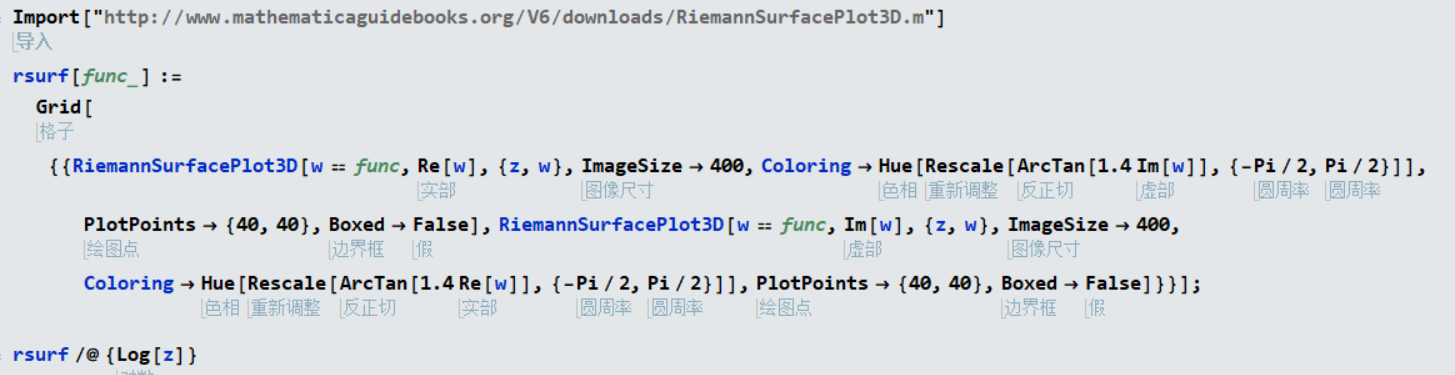
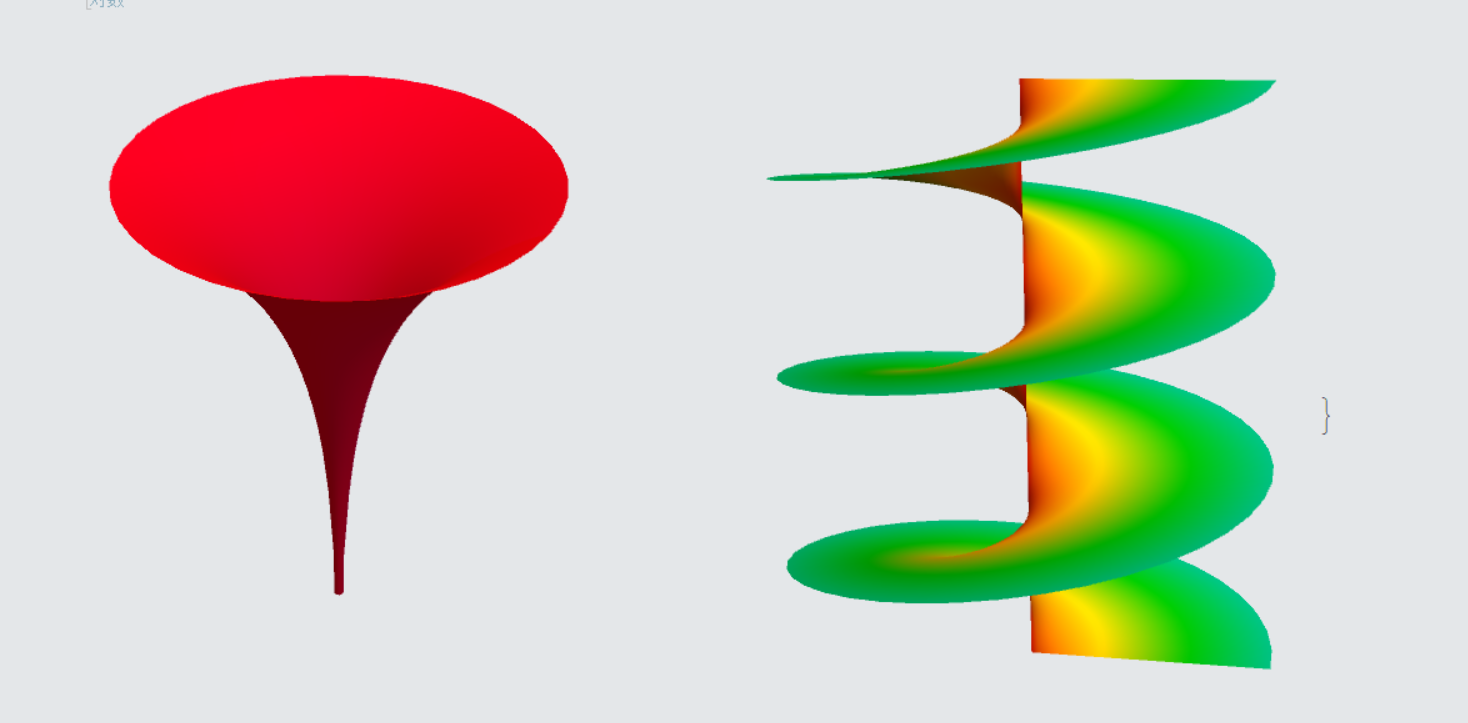
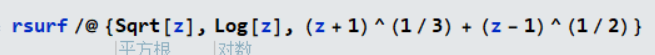
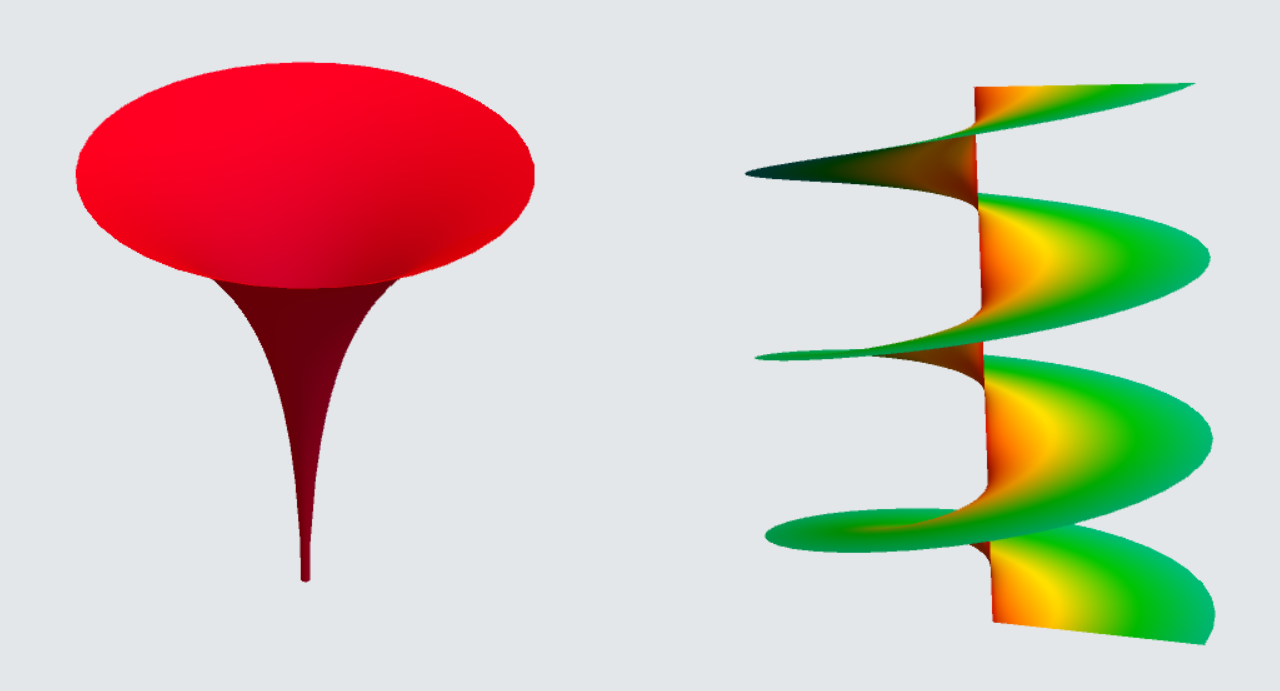
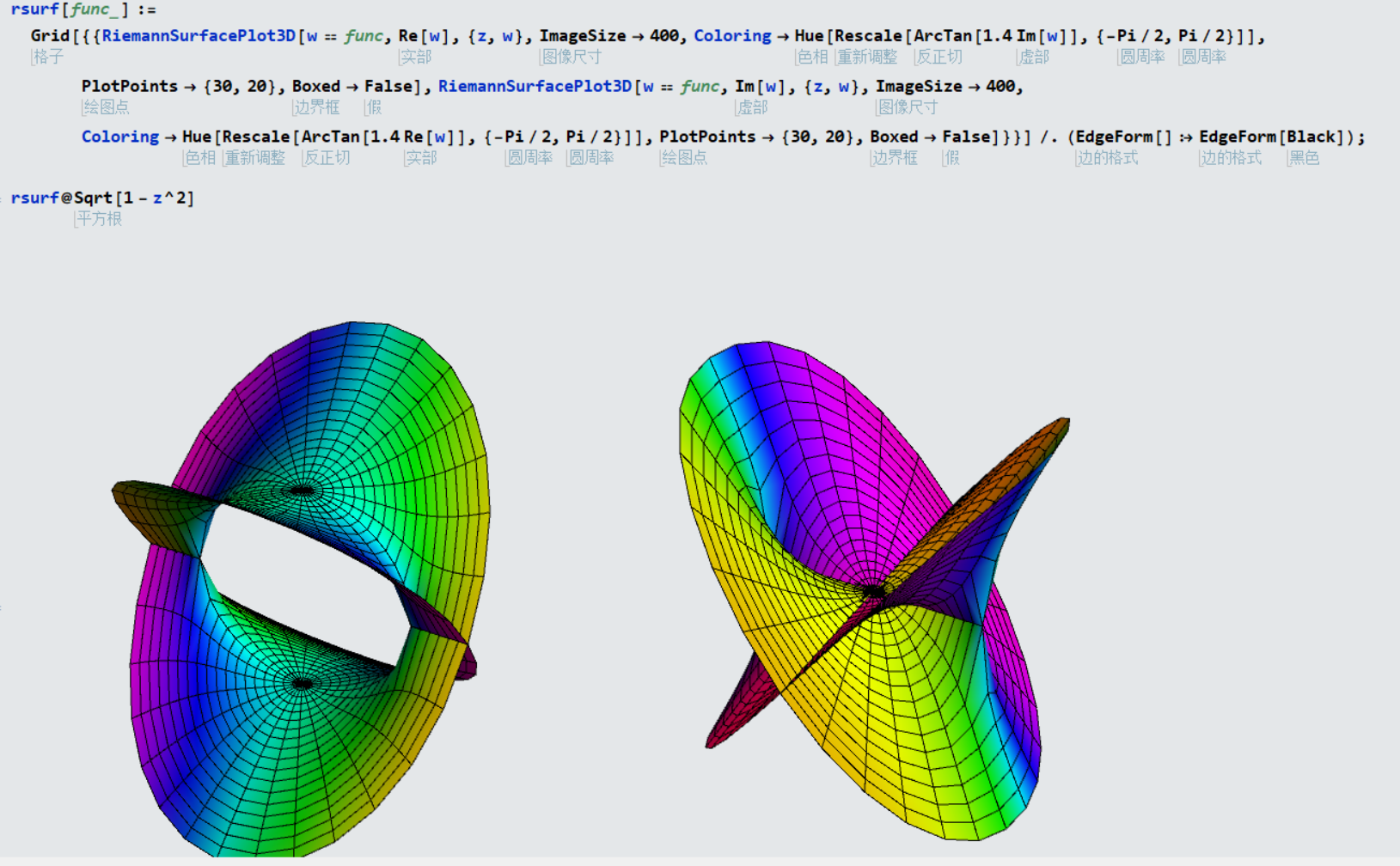
函数多值法绘制

黎曼面其实也就是多值函数的问题,所以可以将多个函数分支绘制到图一张图即可.

png

png

png

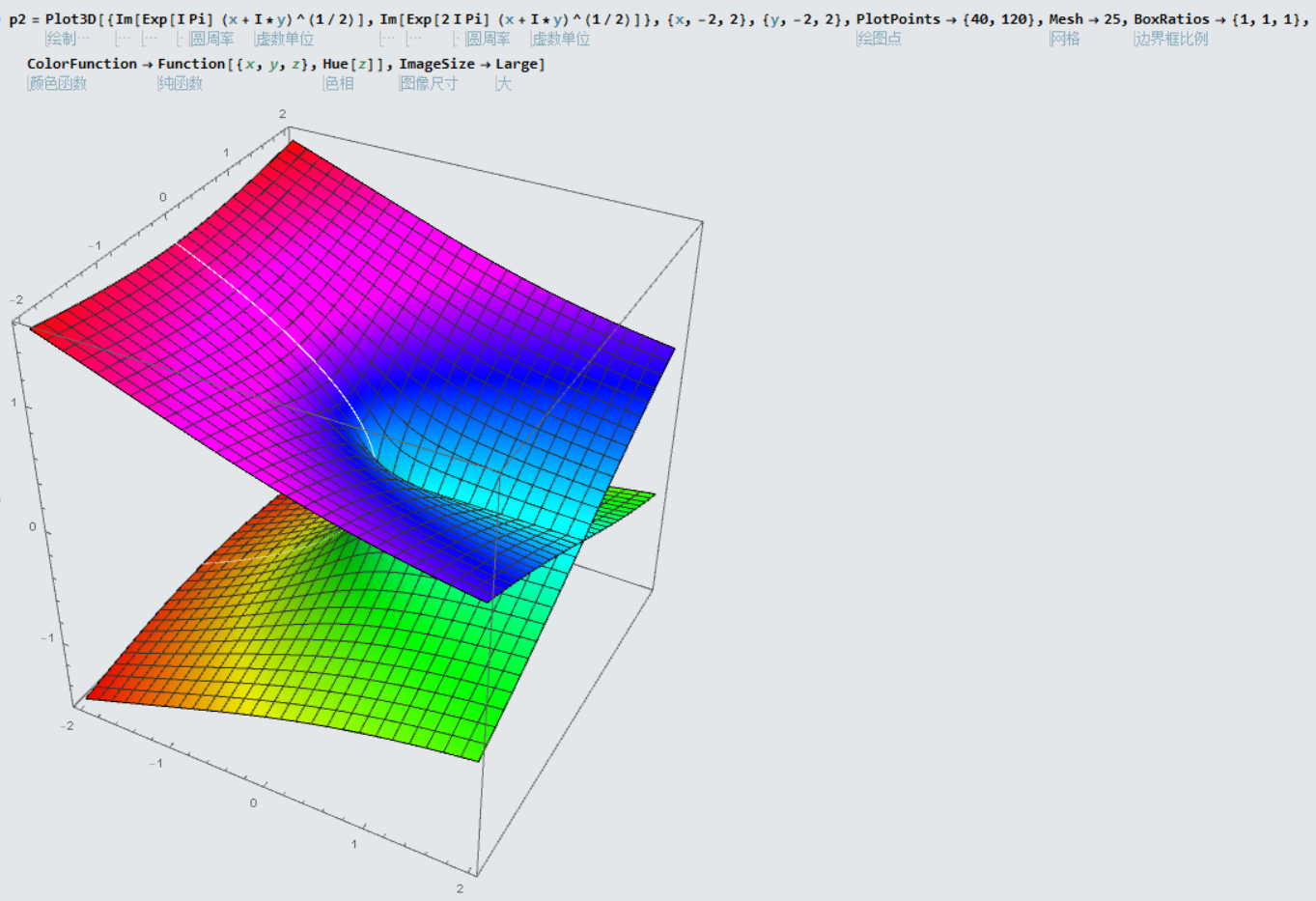
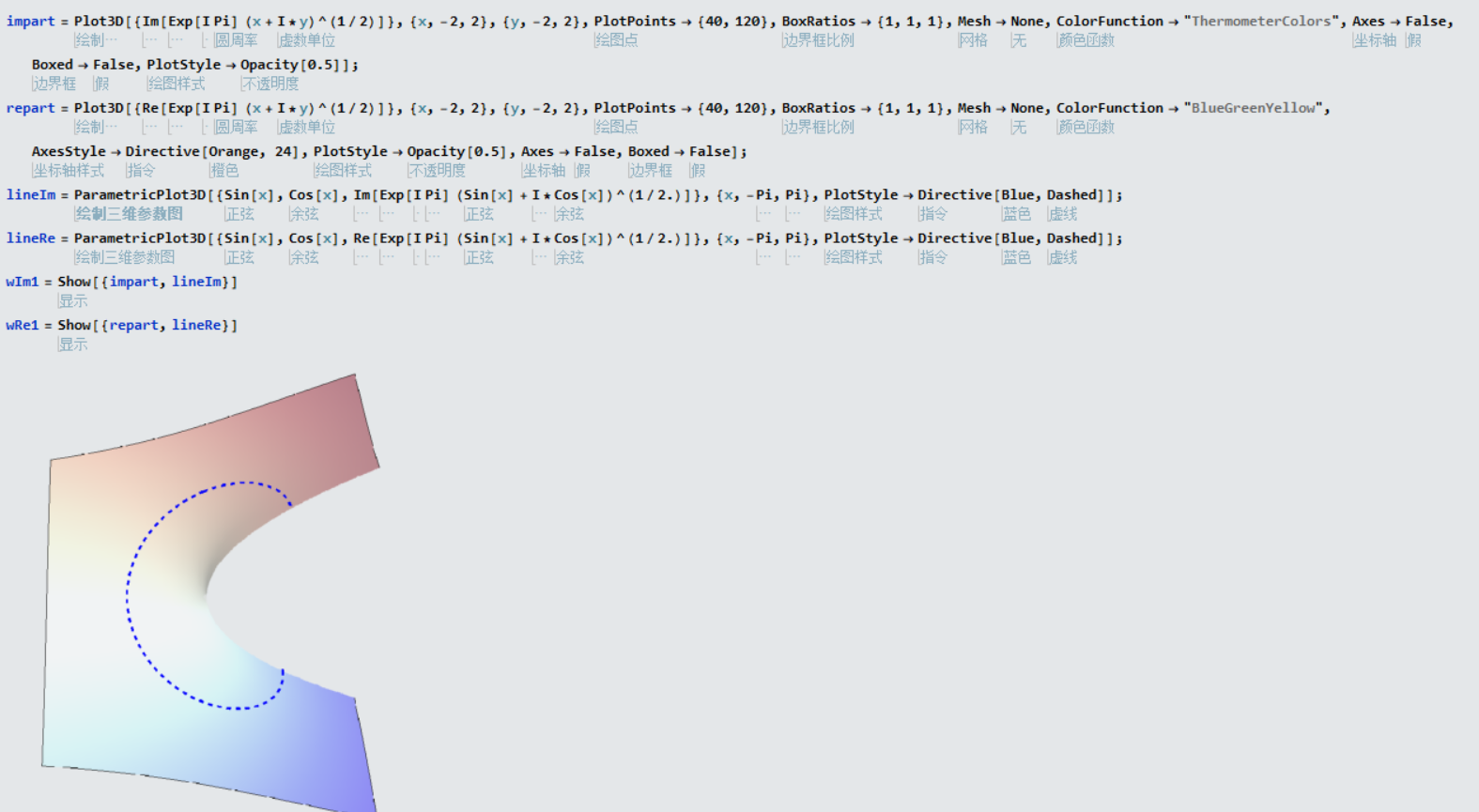
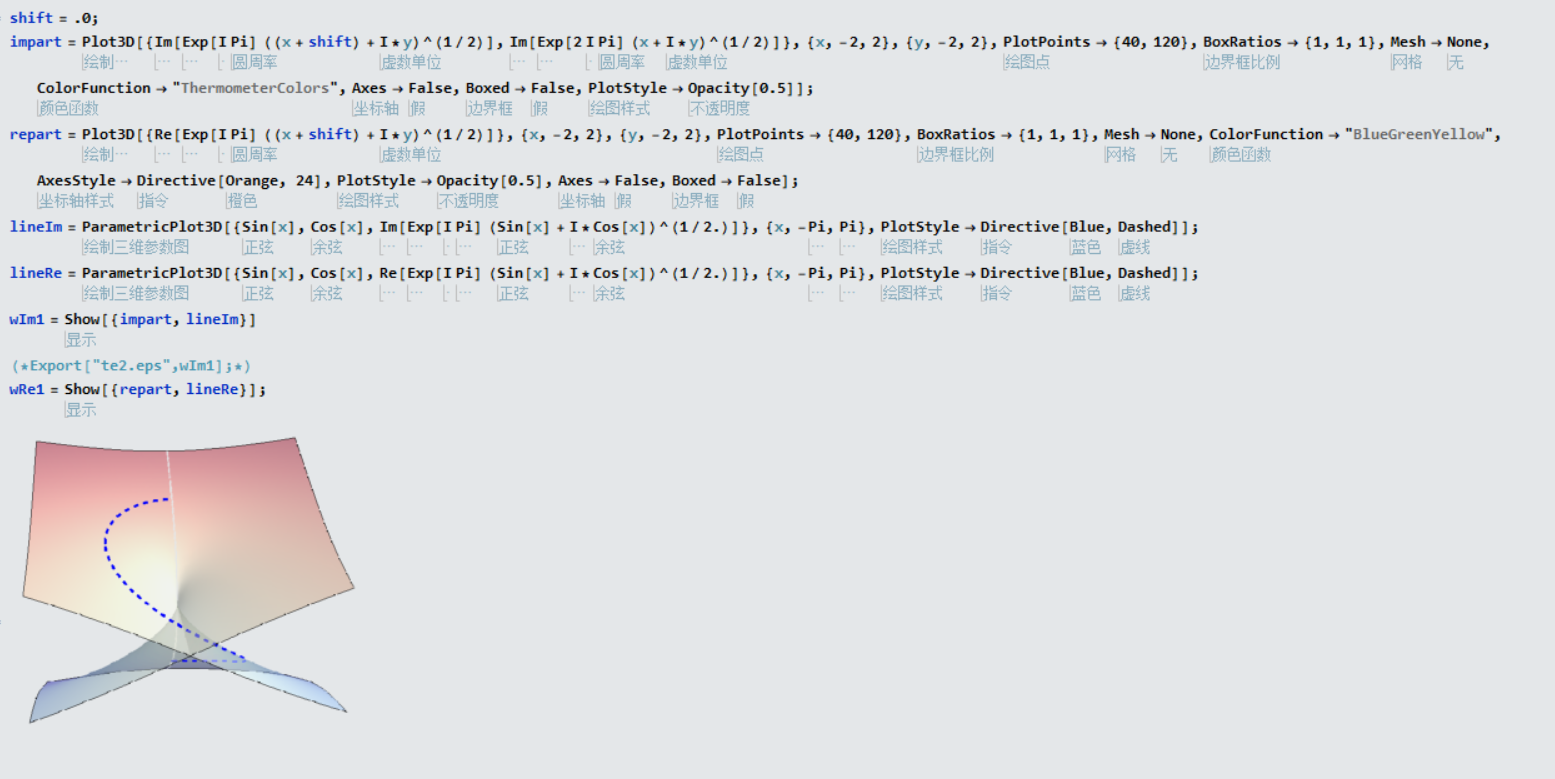
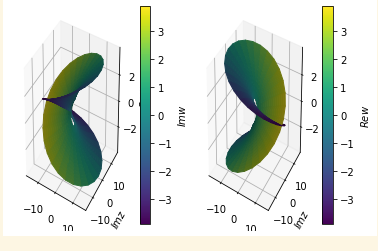
Python绘制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np  
import matplotlib.pyplot as plt  
import matplotlib.cm as cm 
from mpl_toolkits.mplot3d import Axes3D 
 
# compute data to plot 
r, theta = np.mgrid[1:16, -2*np.pi:2*np.pi:50j] 
z = r * np.exp(1j*theta)  
w = np.sqrt(r) * np.exp(1j*theta/2)  
 
# plot data  
fig = plt.figure()  
for plot_index in [1, 2]: 
    if plot_index == 1: 
        z_data, c_data = w.real, w.imag 
        z_comp, c_comp = 'Re', 'Im' 
    else: 
        z_data, c_data = w.imag, w.real 
        z_comp, c_comp = 'Im', 'Re' 
    c_data = (c_data - c_data.min()) / c_data.ptp() 
    colors = cm.viridis(c_data) 
 
    ax = fig.add_subplot(f'12{plot_index}', projection='3d') 
    surf = ax.plot_surface(z.real, z.imag, z_data, facecolors=colors,
                           clim=[z_data.min(), z_data.max()])
    ax.set_xlabel('$Re z$')  
    ax.set_ylabel('$Im z$')   
    ax.set_zlabel(f'${z_comp} w$')  
    cb = plt.colorbar(surf, ax=ax)  
    cb.set_label(f'${c_comp} w$')  
 
plt.show()

png

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
{:.info}

QR Code

Email

yxliphy@gmail.com