BHZ模型Wilson loop计算
这里整理一下计算BHZ模型Wilson loop的代码.
{:.info}
BHZ模型是最初学习拓扑时接触比较早的模型,前面也整理过如何计算BHZ模型的$\mathcal{Z}_2$拓扑不变量,但是其拓扑性质仍然可以通过Wilson loop来进行计算,所以这里就利用Julia来计算一下这个模型的Wilson loop.
代码
1 | using LinearAlgebra,PyPlot,DelimitedFiles |
- 计算结束后,利用`fortran``来将数据进行格式化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36program main
implicit none
integer m1,m2,m3
call main1()
stop
end program
!=======================================================
subroutine main1()
! 读取不明行数的文件
implicit none
integer count,stat
real h1,h2,h3,h4,h5,h22
h1 = 0
h2 = 0
h3 = 0
h22 = 0
open(1,file = "test.dat")
open(2,file = "test-format.dat")
count = 0
do while (.true.)
count = count + 1
h22 = h1
! read(1,*,iostat = STAT)h1,h2,h3,h4,h5
read(1,*,iostat = STAT)h1,h2,h3
! if(h22.ne.h1)write(2,*)"" ! 在这里加空行是为了gnuplot绘制密度图
! write(2,999)h1,h2,h3,h4,h5 ! 数据格式化
write(2,999)h1,h2,h3 ! 数据格式化
if(stat .ne. 0) exit ! 当这个参数不为零的时候,证明读取到文件结尾
end do
! write(*,*)h1,h2,h3
! write(*,*)count
close(1)
close(2)
999 format(5f11.6)
return
end subroutine main1
绘图
1 | set encoding iso_8859_1 |
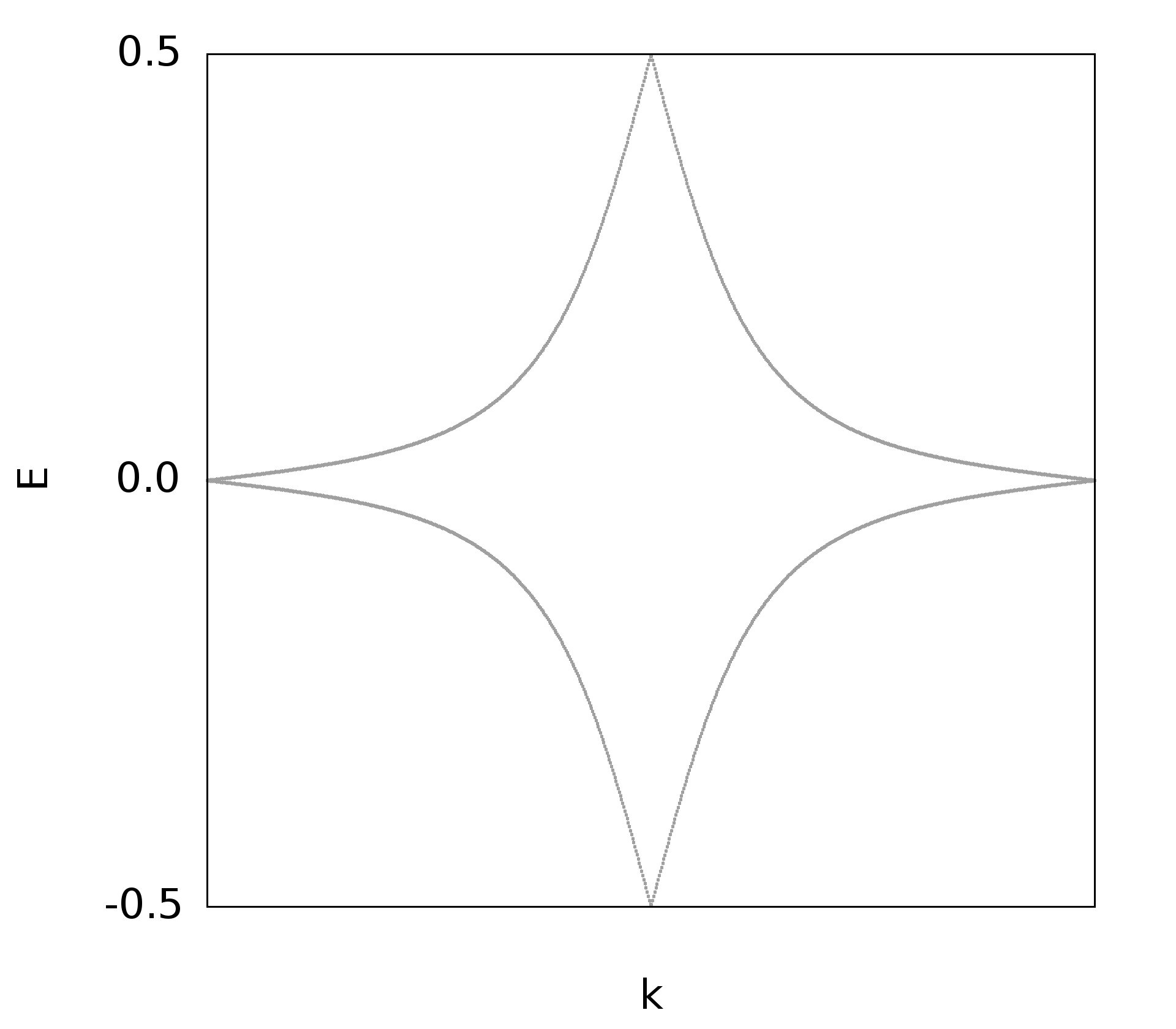
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Yu-Xuan's Blog!
评论









