学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.

基本概念

共轭

一个元素$a,b,c$是群$\mathcal{G}$的群元$(a,b,c)\in\mathcal{G}$,加入下列关系成立

\[a=c\circ b\circ c^{-1}\label{eq1}\]

那么就说群元$a$与$b$之间是共轭的.上式中的$\quad\circ\quad$代表的是群元的操作.

类

利用(\ref{eq1})的关系,将所有与群元$b$共轭的群元划分成一组,那么这一组叫做一个类.

\[\mathcal{C}_{a}=\left\{a_{i} \mid a, b \in \mathcal{G} \wedge a_{i}=b \circ a \circ b^{-1} \wedge a \text { fixed }\right\}\]

陪集

假设$\mathcal{U}$是群$\mathcal{G}$的子群,$a$是$\mathcal{G}$中的元素,那么$a\mathcal{U}$代表元素$a$和群$\mathcal{U}$中的每一个元素相操作,形成一个集合,叫做左陪集.那么相应的$\mathcal{U}a$就叫做右陪集

\[\begin{array}{ll} a \mathcal{U}=\{a \circ p \mid p \in \mathcal{U} \subseteq \mathcal{G}\}, & a \in \mathcal{G} \\ \mathcal{U} a=\{p \circ a \mid p \in \mathcal{U} \subseteq \mathcal{G}\}, & a \in \mathcal{G} \end{array}\]

陪集有一个很重的性质：任意两个陪集，它们要么是完全相同的，要么完全没有公共元素；也就是说群中的一个群元，它只可能属于一个陪集。这个性质对左右陪集都是成立的。

子群

• 群$G$中的一些元素组成一个集合$H$,如果这些元素仍然满足群的定义,那么$H$就是$G$的一个子群.

一个群它自身和单位元一定是其子群,这样的子群叫做非正规子群(improper subgroup),其余的子群叫做正规子群(proper subgroup).

阿贝尔群

• 如果一个群中的元素满足$G_1G_2=G_2G_1$则成这个群是阿贝尔群.

拉格朗日定理

• 群$G$的子群的阶数,一定是群$G$阶数的因子.

不变子群

首先给出书上不变子群的定义

解释一下,就是首先这个子群$\mathcal{S}$的所有元素,在$x\in\mathcal{G}$的共轭操作下,还是它自己,这里要强调的是,这个关系要对所有的$x\in\mathcal{G}$都成立才可以,这就是不变子群的特殊之处.

商群(Factor Group)

既然前面提到了,对于陪集来说,它们之间要么是相同的,要么是完全没有交集,利用这个性质,可以简单的将陪集想象成基矢,类似于坐标空间中的基矢,只不过这个时候的基矢就是我们提到的陪集,那么就可以将整个群在这些基矢上进行分解,也就是图中(3.17)所表示的含义,至于这个基矢的数量可以参考陪集中定理8的第六条.

将这些分解的陪集整合到一起,可以形成一个集合$\mathcal{G}/\mathcal{S}={g_1\mathcal{S},g_2\mathcal{S},\dots,g_N\mathcal{S}}$,给这个集合起个名字叫做商集.

在上面对群$\mathcal{G}$进行基矢分解的时候,选取的是它的任意子群$\mathcal{S}$,前面已经介绍过不变子群的概念,那么现在就将这个分解在不变子群上进行,不变子群利用特殊标记$\mathcal{N}$来表示.

当这个分解在不变子群$\mathcal{N}$上进行时,会发现最后产生的这个商集它又会存在一些额外的性质,简单的说就是这个集合中的元素满足构成群的四个基本条件,所以就称之为商群.最开始学群论的时候,所接触的群元都是一个一个的操作元,但是商群在这里就有一些不同,从上面构成商集的过程来看,商群中的每一个群元(操作),其实对应的是群$\mathcal{G}$的一些群元(操作)的集合,也就是说群$\mathcal{G}$中的多个操作,现在从商群的角度看其实就是商群中的一个群元(操作),好像形成了多对一的映射关系(这里仅仅就是我从群元关系的角度进行的理解,我也不确定用映射这个词是否是正确的).

接下来就利用GTPack这个包,来计算一个商群的实例.关于这个包的下载和安装,可以看我这篇Mathematica群论工具GTPack安装及使用博客

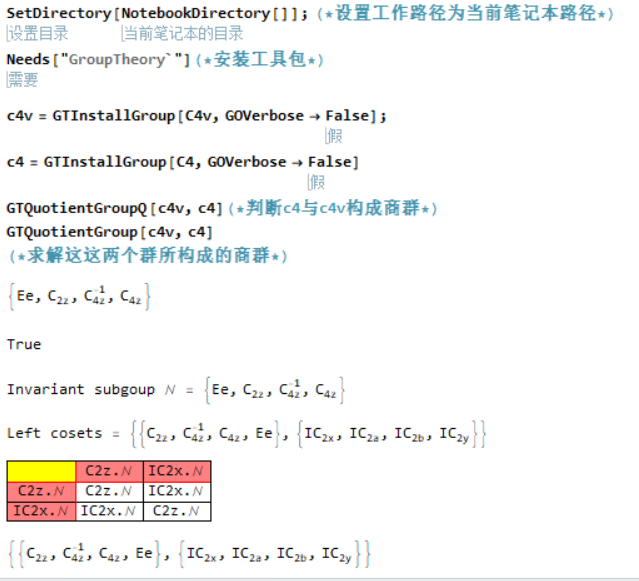
计算的代码可以点击这里下载

如果$\theta$是$\mathbf{G}$到$\mathbf{G}^{‘}$的同态映射,$\mathbf{H}$是$\theta$的Kernel,那么$\mathbf{H}$是群$\mathbf{G}$的不变子群,且$\mathbf{G}^{‘}$与商群$\mathbf{G}/\mathbf{H}$是同构的.

如果$\mathbf{H}$是群$\mathbf{G}$的不变子群,且$\theta$会将群$\mathbf{G}$映射到$\mathbf{G}/\mathbf{H}$上,那么$\theta G=G\mathbf{H}\quad,G\in\mathbf{G}$,此时$\theta$是个同态映射,其对应的Kernel是子群$\mathbf{H}$.

Homomorphism

存在两个群$G$与$G^{‘}$,如果在$G$与$G^{‘}$有一个映射关系$\theta$且仍然满足群元素的运算关系,那么这个映射称为同态(Homomorphism).

\[(\theta A_i)(\theta A_j)=\theta(A_iA_j)\quad \text{for all }A_i,A_j\in G\]

阶数较小的群称为阶数较大的群的同态像(homomorph). 把$G$中映射到$G^{‘}$单位元素上的所有元素的集合, 称为同态核(kernel of the homomorphism).

Isomorphism

如果这个映射使得群$G$与$G^{‘}$中的元素满足一一对应关系, 那么此时的$\theta$叫做同构(Isomorphism), 两个群之间是同构的(isomorphic).

automorphism

如果两个群$G$与$G^{‘}$是完全相同的, 那么也就是$\theta$是一个群到自身的映射, 那么这种映射称为自同构(automorphism).

如果$\theta$是自同构映射, 且映射满足

\[\theta G=XGX^{-1};\text{for }X\in G\]

此时可以看出自同构是等价于共轭的, 那么这种情况称为内自同构(inner automorphism), 其余的情况就称为外自同构(outer automorphisms).

实例

If $G$ = $G_6$ and $G^{‘}= G_2 = {E,A^{‘}}$, then the mapping

\[\theta(E)= \theta(D)= \theta(F)= E\\ \theta(A)= \theta(B)= \theta(C)= A^{'}\]

is a homomorphism of $G_6$ onto $G_2$.

The groups $C_{3v}$, $D_3$ and $S_3$ are isomorphic: They have the same order and share the same multiplication table.

If $\theta(E)= E, \theta(A)= B, (B)= C, \theta(C)= A, \theta(D)= F$, and $\theta(F)= D$, the mapping is an automorphism of $G_6$ onto itself.

Kernel

• 如果$\theta$是$\mathbf{G}$到$\mathbf{G}^{‘}$的同态映射,$\theta\mathbf{G}=\mathbf{G}^{‘}$,映射$\theta$的Kernel就是群$\mathbf{G}$中映射到群$\mathbf{G}^{‘}$单位元的群元.

这里可以知道,对于同构映射,其Kernel只有一个群元素.

内自同构(Inner automorphism)

• 一个映射$\beta$将群$\mathbf{G}$映射到它自身,$\beta G=BGB^{-1}$,这里$G\in\mathbf{G}$,$B$是群$\mathbf{G}$中的一个固定元素,这是一个自同构,而通过这种共轭方式产生的自同构称为内自同构.

简单群(simple group)

• 如果一个群没有正规不变子群,就称为简单群,若没有正规不变阿贝尔子群,则成为半简单群(semi-simple).

外直积

群$\mathbf{G}$有两个子群$\mathbf{H},\mathbf{K}$,存在如下关系

• (1):$H\in\mathbf{H},K\in\mathbf{K}\rightarrow HK=KH$,
• (2):群$\mathbf{G}$中的所有元素$G\in\mathbf{G}$可以表示为$G=HK,H\in\mathbf{H},K\in\mathbf{K}$,
• (3):两个子群的交集为$\mathbf{K}\cap\mathbf{H}={E}$,这个单位元素$E\in\mathbf{G}$.

此时群$\mathbf{G}$叫做$\mathbf{K},\mathbf{H}$的外直积,$\mathbf{G}=\mathbf{K}\otimes\mathbf{H}$

内直积

• 外直积$\mathbf{H}\otimes\mathbf{H}$群的一个子群$\mathbf{G}$与群$\mathbf{H}$是同构的(isomorphic),那么称$\mathbf{G}$是$\mathbf{H}$自身的内直积$\mathbf{G}=\mathbf{H}\boxtimes\mathbf{H}$.

这里再强调一下,此时群$\mathbf{G}$是外直积群的子群.

半直积

$\mathbf{H},\mathbf{K}$是群$\mathbf{G}$的子群,当满足

• (1):$K\in\mathbf{K},K\mathbf{H}=\mathbf{H}K$,
• (2):所有的$G\in\mathbf{G}$可以表示为$G=HK$且$K\in\mathbf{K},H\in\mathbf{H}$,
• (3):子群$\mathbf{H},\mathbf{K}$的交集为$\mathbf{K}\cap\mathbf{H}={E}$,

此时称$\mathbf{G}$是子群$\mathbf{H},\mathbf{K}$的半直积$\mathbf{G}=\mathbf{H}\land\mathbf{K}$.这里可以看出子群$\mathbf{H}$是群$\mathbf{G}$的不变子群,但是$\mathbf{K}$却不必是个不变子群.

全形(holomorph)

• 一个半直积$\mathbf{G}\land\mathbf{A}(\mathbf{G})$叫做群$\mathbf{G}$的同形,这里的$\mathbf{A}(\mathbf{G})$是群$\mathbf{G}$的自同构群.

不变子空间

• 如果$\gamma$是$\mathbf{G}$的一个表示,$\mathbf{T}=\gamma\mathbf{G}$是作用在矢量空间$\mathbf{V}$上的非奇异线性算符,在$\mathbf{T}$下$\mathbf{U}$称为$\mathbf{V}$的不变子空间,当其满足下面条件: (1):$\mathbf{U}$是$\mathbf{V}$的矢量子空间, (2):对所有的$\mathbf{x}\in\mathbf{U}$有$\mathbf{T}_G\mathbf{x}\in\mathbf{U}$,这里的$\mathbf{T}_G\in\mathbf{T}$.

群表示

• 一个群的不可约表示数目等于群类的数目
• 所有不可约表示维数的平方和等于群的阶数$\sum_{i=1}^{r}d_i^2=\rvert\mathbf{G}\rvert$

点群

• 三维的点群是指对称操作作用在一个点上,保持变换对象的距离和角度不变.
• 当一个点群只包含转动操作的时候,被称为三维正规转动群,它与行列式=+1的SO(3)群是同构的.
• 当一个群包含所有的转动与反演操作的乘积被称为三维转动群,它与所有$3\times 3$的O(3)群是同构的.

布拉菲点阵

三维空间中一共会存在14种布拉菲点阵,而着14种点阵又可以分为7大晶系,每个晶系满足不同的对称操作

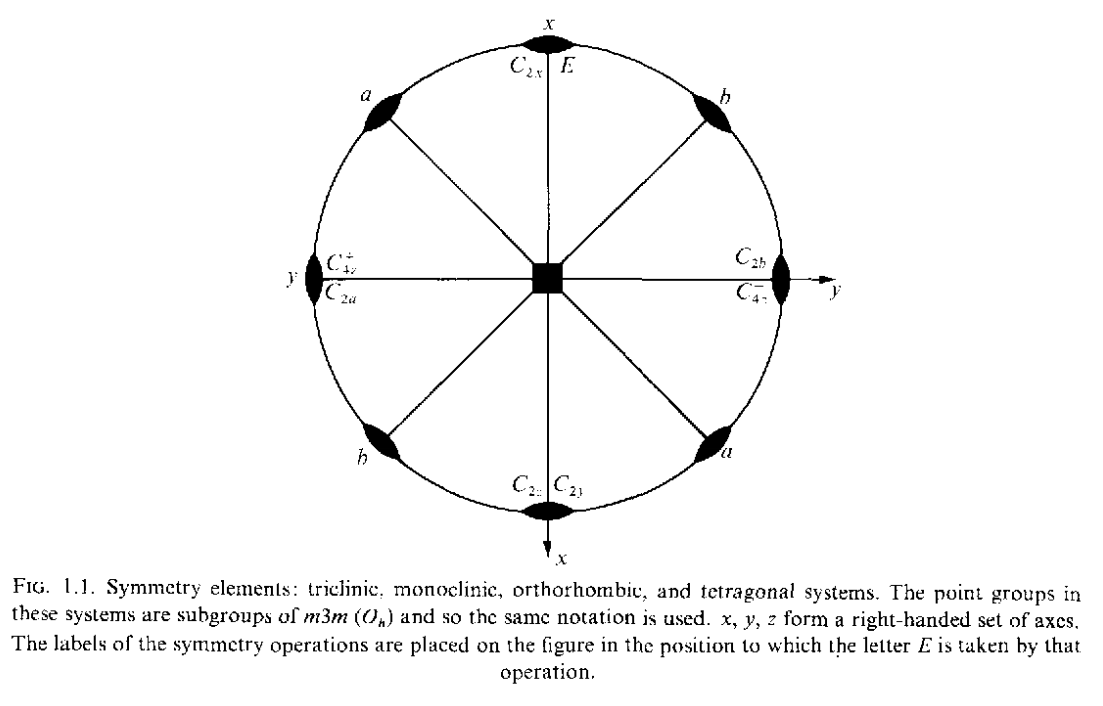
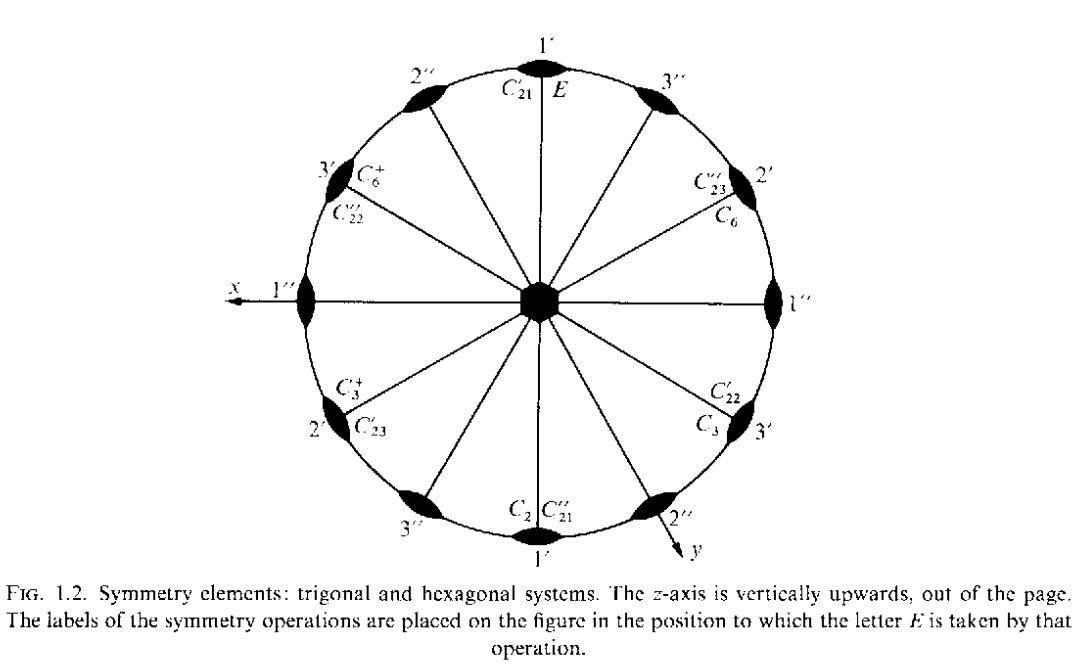
Table 1.2中操作元素分成了两列,右侧的一列就是左侧列组合反演对称操作I之后的结果.$C_{nr}^{-}$表示绕着$r$轴顺时针旋转$2\pi/n$度,而$C_{nr}^+$则表示顺时针转动.在上面的标记中反射面标记为$\sigma$,而其它的旋转反射标记为$S$.

$\sigma=IC_2,IC_3^\pm=S_6^\mp$

$S^+_n$表示先逆时针转动$2\pi/n$然后再通过垂直于旋转轴的面进行反射(reflection),从而可以得到

\[IC^{+}_{n}=\sigma C_2C^{+}_{n}=\sigma(C_{2n}^+)^{n+2}=(S_{2n}^-)^{n+2}\]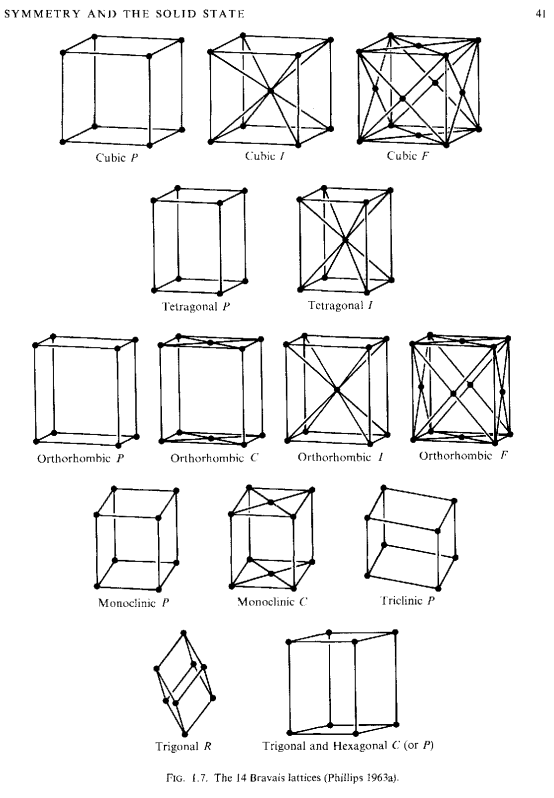

图中Table 1.2分别给出了这些晶系满足的对称操作和其对应的点群标记.上面的点群操作对应的图示如下

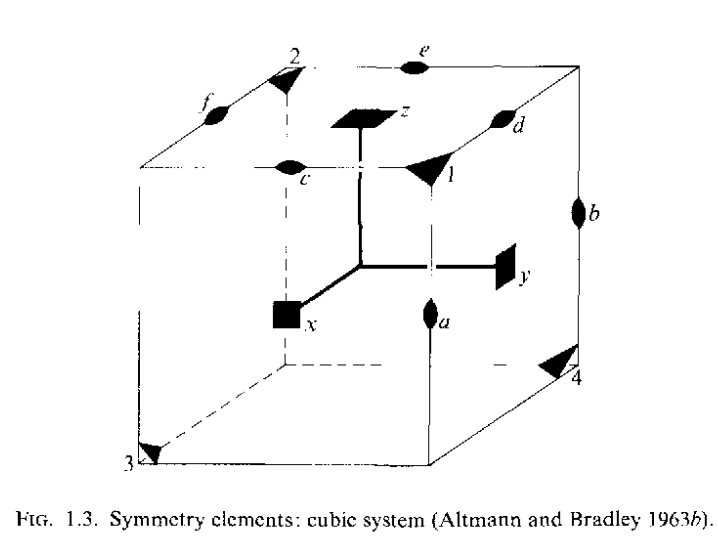
下面给出三维空间中的32个点群,虽然在Table1.2中给出了每个晶系存在的对称操作,但是对于每个晶系可以通过选定特定的某一些操作来构成一个群,最终可以就可以得到空间中的32个点群.

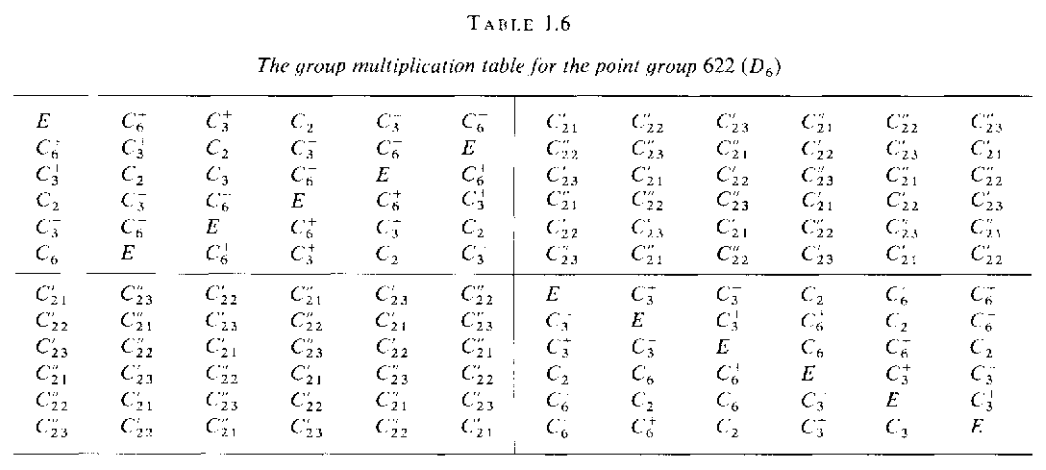
下面给出点群432(O)h和622($D_6$)的群乘法表,这两个点群仅包含转动操作,其它仅包含转动操作的点群都是他们的子群,因此可以从这两个表中快速得到其它点群对应的群乘法表

空间群

在前面介绍的布拉菲点阵,在相同的方向上,每个点都具有完全相同的环境,这就可以和晶体联系起来,其就是由许多完全相同的结构组成的,将这些结构抽象成点,那么这些整齐规则的排列也就对应着布拉菲点阵.

这里强调一下,布拉菲点阵是抽象出来的数学点阵,所以并不代表在实际材料中,布拉菲格点就处在原子的中心位置,也不是说布拉菲点阵会被原子占据.

选定一个中心位置,那么对于每个布拉菲点阵,当确定了基矢之后,点阵上的每个点就可以通过一个矢量来描述

\[\mathbf{t}=n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3,\quad n\in\text{整数}\]

当$n_i$遍历所有整数的时候,就可以遍历布拉菲格点上的每一个点.由$\mathbf{t}$确定的平移操作可以构成一个无限群,它正是布拉菲点阵的平移群.除了平移操作之外.布拉菲点阵还具有点群操作的对称性.点群操作作用在任何一个布拉菲格点上会构成一个点群$\mathbf{P}$,实际上它与晶体系统的点群是全对称的(holosymmetric).在前面七大晶系的表中也已经给出了对应的点群.由于14中布拉菲格子对应的点群$\mathbf{P}$与七大晶系的点群操作是全对称的(holosymmetric),因此一定可以把这14中布拉菲格子归属到对应的晶系中,如上图1.7所示.

晶体的点群对称性一定要和其对应的布拉菲格点的对称性相容,因此总共只有32个晶体点群.

因为三维空间中的布拉菲点阵是无限大的,所以元胞(unit cell)的选取就有很多种方式,通常它是有平行六面体的三条不共面的变构成的,用$\mathbf{a,b,c}$标记.通常在选取元胞的时候,会使得其满足布拉菲点阵的对称性,这种方式确定的元胞可能并不是初基原胞(primitive),它可能会包含多个等价的布拉菲格点,而初基原胞的定义则是其只包含一个布拉菲格点.

由布拉菲点阵基矢$\mathbf{t}_1,\mathbf{t}_2,\mathbf{t}_3$确定的的元胞叫做初基原胞(primitive unit cell).上图1.7中给出的就是传统元胞(conventional unit cell).下面是一个2维情况下初基原胞与传统元胞的区别

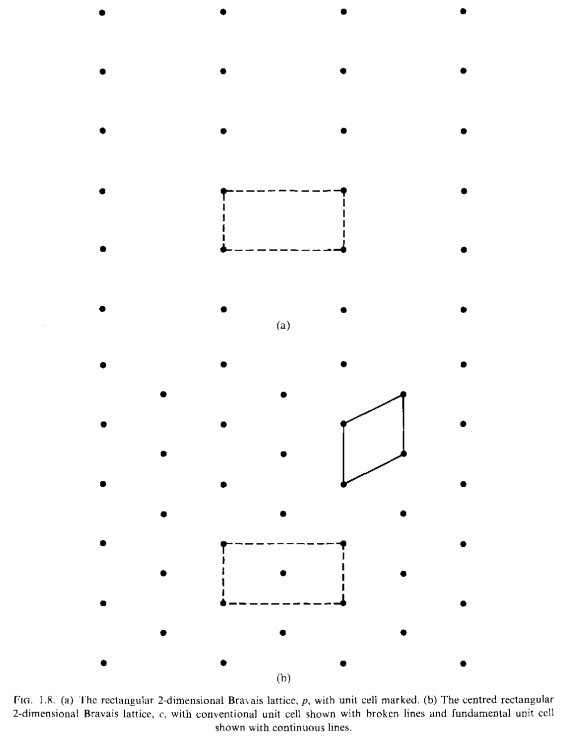
可以发现传统元胞中包含了2个有效格点,然而初基原胞中则仅包含了一个.

这里讨论的布拉菲格点都是一些数学上抽象出来的点,并不具有大小和形状,要想在此基础上实际晶体,就需要在这些格点上放入原子或者分子.因为这些格点所处的环境都是相同的,而且具有周期性结构,所以这些重复的单元就可以组成实际的晶体.但是在放置这些原子或者分子的时候,也是具有对称性要求的,这些放入的原子或者分子具有的对称性一定要和对应布拉菲点阵的点群对称性是相容的.

点式空间群

布拉菲点阵的抽象是用来反映晶体的平移性质,而其具体的布拉菲点阵结构也具有点群对称性,从Table1.3可以看到对于特定的晶系,都有其对应的一些点群,比如cubic晶系共有5个点群,但是从Table1.7又可以看到,cubic晶系中可以有3中不同的布拉菲点阵,因此对每个点阵赋予cubic晶系满足的对称群,就可得到cubic晶系一共可以产生15个点群.将所有的晶体系统都进行考虑之后,这种方式可以构成的空间群的数目为

\[\sum_{i=1}^7n_ip_i\]

这里$n_i$是确定晶系中点群的的数目,$p_i$是晶系中布拉菲点阵的数目.

通过上面这种方式构成的空间群称为点式空间群(symmorphic),它是平移群和点群的半直积,一共有73个点式空间群.

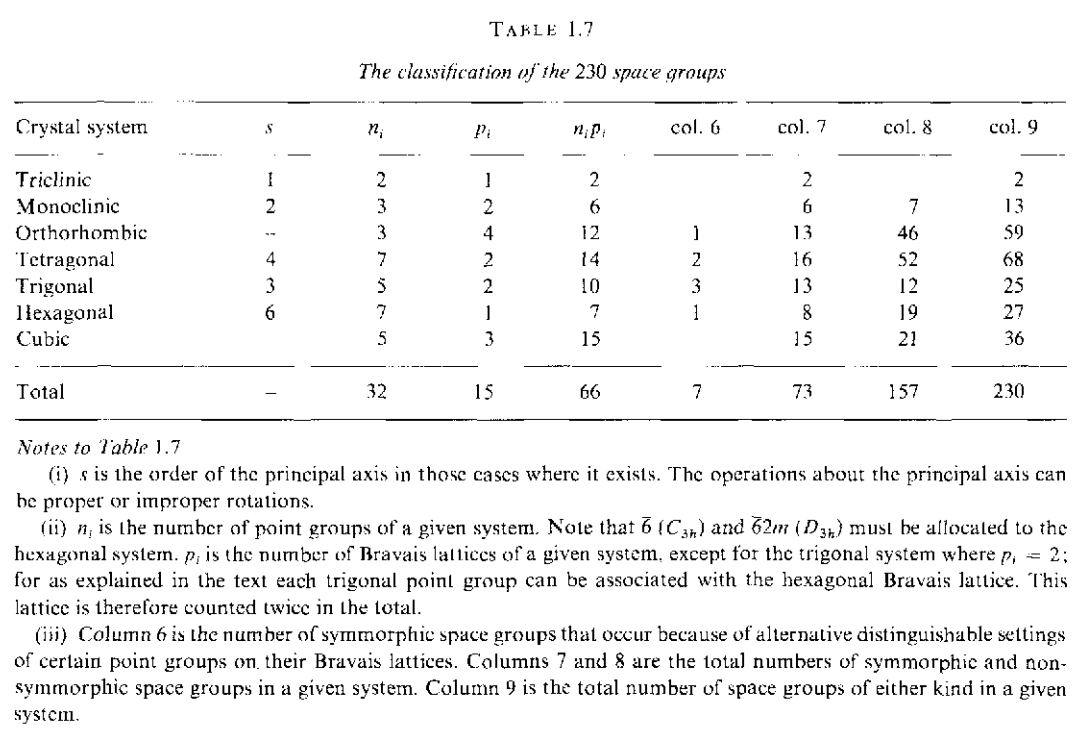
在点式空间群中,点群操作和平移操作时分离开的,点群操作的存在时对晶体的对称操作.

非点式空间群(non-symmorphic)

• 除了上面介绍到的点式空间群,还有一类非点式空间群,它是通过将点式空间群中的反射平面替换成滑移反射(glide reflection),将旋转轴替换为螺旋轴(screw rotation).

滑移反射(glide reflection)操作是有一个反射面m和一个平移操作$v$组合而成,当连续执行两次这样的滑移反射操作,其效果就是一个平移操作,它一定属于布拉菲点阵平移操作群中的一员.

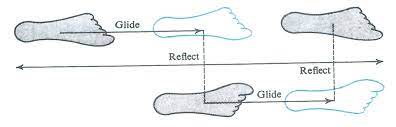
螺旋操作时转动操作$2\pi/n$再结合一个平移操作,当进行n次的螺旋操作之后,其也等价于布拉菲点阵中的一个平移操作元.

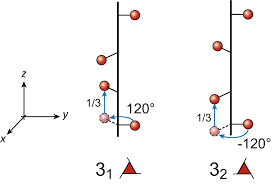
通过考虑滑移反射和螺旋操作之后,会存在157中非点式空间群.这里需要说明一下,滑移反射中的平移操作一定是在自身的反射面中,而螺旋操作中的平移操作一定是沿着转动轴的.157个非点式空间群加上73个点式空间群,最终一共有230个空间群,如Table1.7所示.

空间群操作符号

\[\{\mathbf{R}_1\rvert \mathbf{v}_1\}\mathbf{r}=\mathbf{r}^{'}=\mathbf{R}_1\mathbf{r}+\mathbf{v}_1\]

这里的$\mathbf{R}_1$表示点群操作,$\mathbf{v}_1$则是平移矢量.

\[\{\mathbf{R}_2\rvert\mathbf{v}_2\}\{\mathbf{R}_1\rvert\mathbf{v}_1\}=\{\mathbf{R}_1\mathbf{R}_2\rvert\mathbf{v}_2+\mathbf{R}_2\mathbf{v}_1\}\]

当点群操作$\mathbf{R}$作用到一个空间矢量上之后

\[\mathbf{Rr}=\mathbf{r}^{'}\]

在$\mathbf{r}$和$\mathbf{r}^{‘}$对应的操作上,可以定义函数关系满足

\[g(\mathbf{r}^{'}=f(\mathbf{r})\]

这里的虽然$\mathbf{r}$和$\mathbf{r}^{‘}$是不同的,但是当将两者作为参数进行函数映射之后,对应的函数表达式确实相同的,因此对于点群操作$\mathbf{R}$可以在函数上定义函数空间中的操作算符$\bar{R}$有$g=\bar{R}f$,其存在关系

\[\bar{R}f(\mathbf{r})=f(\mathbf{R}^{-1}\mathbf{r})\]

主动/被动操作

主动操作(active)是固定坐标轴之后变换点的位置

\[\{\mathbf{R}_a\rvert\mathbf{v}\}\mathbf{r}=\mathbf{R}_a\mathbf{r}+\mathbf{v}\] \[\{\mathbf{S}_a\rvert\mathbf{w}\}\{\mathbf{R}_a\rvert\mathbf{v}\}=\{\mathbf{S}_a\mathbf{R}_a\rvert\mathbf{w}+\mathbf{S}_a\mathbf{v}\}\] \[\{\mathbf{R}_a\rvert\mathbf{v}\}^{-1}=\{\mathbf{R}_a^{-1}\rvert-\mathbf{R}_a^{-1}\mathbf{v}\}\]

被动转动是在固定操作点的情况下操作坐标轴进行变化

\[[\mathbf{R}_p\rvert\mathbf{v}]\mathbf{r}=\mathbf{R}_p\mathbf{r}-\mathbf{R}_p\mathbf{v}\] \[[\mathbf{S}_p\rvert\mathbf{w}][\mathbf{R}_p\rvert\mathbf{v}]=[\mathbf{S}_p\mathbf{R}_p\rvert\mathbf{v}+\mathbf{R}_p\mathbf{w}]\] \[[\mathbf{R}_p\rvert\mathbf{v}]^{-1}=[\mathbf{R}_p^{-1}\rvert-\mathbf{R}_p\mathbf{v}]\]

holosymmetric

对于一个给定的晶体系统,如果一个点群$\mathbf{P}$包含了这个系统所有的对称操作,那么就称$\mathbf{P}$是系统的全对称点群(holosymmetric point group).

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。