学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.
点群操作基函数
球谐函数
对于点群操作,可以找到对应的一些基函数来满足变换性质,从而在基函数的基础上可以得到操作的矩阵表示,这里就以球谐函数为出发点,来寻找点群操作的基函数.首先球谐函数的定义为
\[Y_l^m(\theta,\phi)=\sqrt{\frac{(2l+1)(l-\rvert m\rvert)!}{4\pi(l+\rvert m\rvert)!}}P_l^m(\cos\theta)\exp(im\phi)\]这里$P_l^m(\cos\theta)$是勒让德函数
\[P_l^m(\cos\theta)=\frac{1}{2^ll!}\sin^{\rvert m\rvert}\theta\frac{d^{l+\rvert m\rvert}}{(d\cos\theta)^{l+\rvert m\rvert}}\{(\cos^2\theta-1)^l\}\]一个转动操作$R$可以通过欧拉角($\alpha,\beta,\gamma$)来表示:首先进行绕z轴的主动转动角为$\alpha,(0\le\alpha\le2\pi)$,接下来绕着y轴进行主动转动$\beta,(0\le\beta\le\pi)$,最后绕着z轴主动转动$\gamma,(0\le\gamma\le 2\pi)$.在三维的求坐标系中,第一次转动$\alpha$对应着$(r,\theta,\phi)\rightarrow(r,\theta,\phi+\alpha)$,第二次转动$\beta$对应$(r,\theta,0)\rightarrow (r,\theta+\beta,0)$,第三次转动$\gamma$对应着$(r,\theta,\phi)\rightarrow (r,\theta,\phi+\gamma)$.
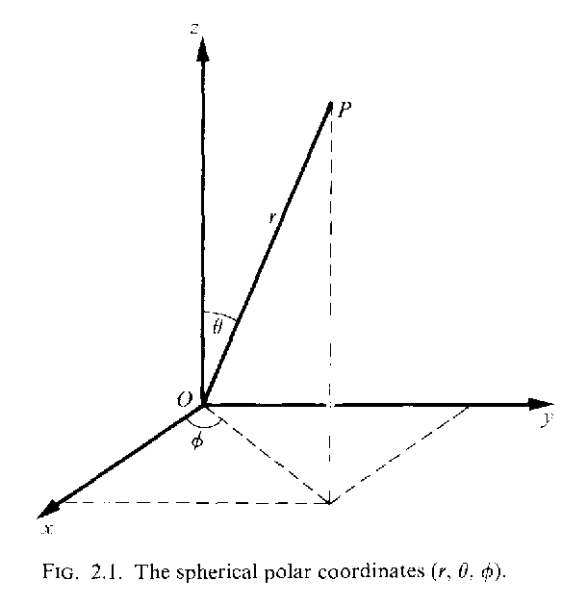
一个转动操作$R(\alpha,\beta,\gamma)$就对应着连续进行这三个操作,这里采用主动坐标系(active),此时的转动方向都是逆时针方向进行的.当将一个转动操作作用到球谐函数上之后
\[R(\alpha,\beta,\gamma)Y^m_l(\theta,\phi)=\sum_{n=-l}^{l}Y^n_l(\theta,\phi)\mathcal{D}^l\{R(\alpha,\beta,\gamma)\}_{mn}\]这里的矩阵$\mathcal{D}^l$为
\[\mathcal{D}^l\{R(\alpha,\beta,\gamma)\}_{nm}=C_{nm}\exp(-in\gamma)d^l(\beta)_{nm}\exp(-im\alpha),\quad C_{nm}=(i^{\rvert n\rvert+n})(i^{-\rvert m\rvert -m})\] \[d^l(\beta)_{nm}=\sum_k\frac{(-1)^{k-m+n}\sqrt{(l+n)!(l+m)!(l-n)!(l-m)!}}{(l-n-k)!(l+m-k)!k!(k-m+n)!}\cos^{2l+m-n-2k}(\frac{1}{2}\beta)\sin^{2k+n-m}(\frac{1}{2}\beta)\]$k=\text{max}{0,(m-n)}\rightarrow\text{min}{(l-n),(l+m)}$,对于三维空间中的转动操作$R(\alpha,\beta,\gamma)$,当整数$l$确定之后,只有唯一的一个$\mathcal{D}^l{R(\alpha,\beta,\gamma)}$与之相对应.对于一个给定的$l$值的矩阵$\mathcal{D}^l{R(\alpha,\beta,\gamma)}$形成了一个$(2l+1)$维的旋转群$R(\alpha,\beta,\gamma)$的表示,而球谐函数$Y_l^m(\theta,\phi)(-l\le m\le l)$则是这个表示的基矢.矩阵元素$d^l(\beta)_{nm}$会有下面的对称关系
\[d^l(\beta)_{nm}=d^l(\beta)_{-m,-n}=(-1)^{m+n}d^l(\beta)_{mn}\]因此在计算$d^l(\beta)$的时候,只需要计算$-l\le m\le l,\rvert m\rvert\le n\le l$范围内的值即可.这里来主要关注$\beta=0,\frac{1}{2}\pi,\pi$处的性质,原因有两个:任意$\beta$角度下的值都可以被转换到$\beta=\frac{1}{2}\pi$计算,对于晶体点群操作,总可以选择一个合适的轴,将$\beta$角变为$0,\frac{1}{2}\pi,\pi$中的一个值.
- 当$\beta=0$的时候:
- 当$\beta=\pi$的时候:
为了研究球谐函数在晶体点群操作下的性质,还需要考虑反演操作$I$
\[IY^l_m(\theta,\phi)=(-1)^lY^l_m(\theta,\phi)\]下面给出一个点群操作对应的欧拉角
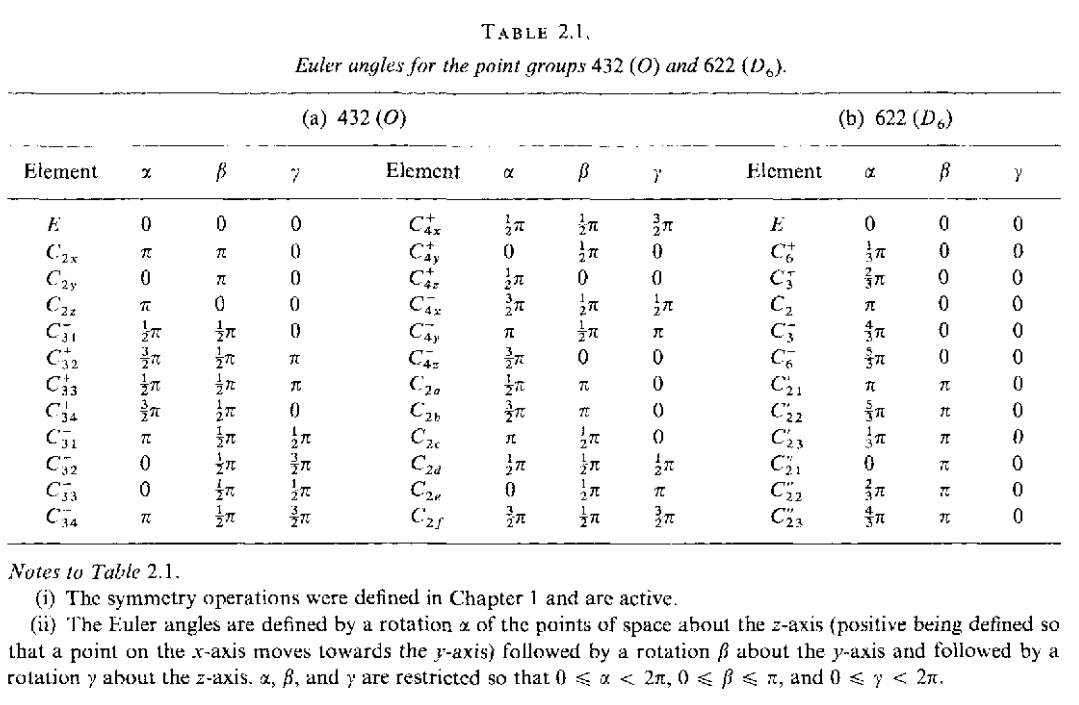
基函数寻找
对一个群$\mathbf{G}$其对应的阶数为$\rvert\mathbf{G}\rvert$,其对应的不可约表示$\Gamma^i{R\rightarrow\mathbf{D}^i(R)}$已知,这里的$\mathbf{D}^i$是是群元$R$的矩阵表示,对应的维度是$d_i$,而现在就要找到一组合适的基矢$\langle\phi_1^i,\phi_2^i,\cdots,\phi_{d_i}^i\rvert$满足
\[R\phi_s^i=\sum_{t=1}^{d_i}\phi_t^i\mathbf{D}^i(R)_{ts},\quad R\in\mathbf{G}\]这里的$\phi_s^i$是属于不可约表示$\Gamma^i$的第$s$行的symmetry-adapted function,这些所有的$\phi_s^i$构成了一个完整的线性空间$V$.
首先来定义一个元素$W^i_{ts}$:
\[W^i_{ts}=\frac{d_i}{\rvert\mathbf{G}\rvert}\sum_{R\in\mathbf{G}}\mathbf{D}^i(R)_{ts}^*R\]这里的求和是对所有$R\in\mathbf{G}$进行的,从它的定义中可以看出它是由一些数和群$\mathbf{G}$中的操作群元组成的.
- 定理:如果$\phi$是$V$中的任意一个函数满足$W^i_{ss}\phi\neq 0$($s$是固定的,可以遍历1到$d_i$),那么函数$W^i_{ts}\phi=\phi^i_t,t=1\rightarrow d_i$就构成了不可约表示$\Gamma^i$的一个基矢.
这里可以将$\phi$看做是symmetry-adapted function的生成函数,$W_{ss}^i$是投影算符.
点群基函数寻找
对于一个点群$\mathbf{G}$其中的元素为$R,S,\cdots$,其对应的矩阵表示为$\mathbf{D}^i(R),\mathbf{D}^i(S),\cdots$,此时选择球谐函数$Y_l^m(\theta,\phi)$作为生成函数,来计算投影算符对球谐函数的作用
\[W^i_{ts}Y_l^m(\theta,\phi)=\frac{d_i}{\rvert \mathbf{G}\rvert}\sum_{R\in\mathbf{G}}\mathbf{D}^i(R)_{ts}^*RY_l^m(\theta,\phi)\]此时需要计算$RY_l^m(\theta,\phi)$,这里的$R$表示正规转动操作或者反演操作,它们对球谐函数的作用在前面已经给出,如果$R$是一个非正规转动(improper)可以将其表示为$R=IQ$,此时需要同时计算$QY_l^m(\theta,\phi),IY_l^m(\theta,\phi)$,反演操作不过是简单的加上一个$(-1)^l$的因子,最终可以将上式变为
\[W^i_{ts}Y_l^m(\theta,\phi)=\frac{d_i}{\rvert\mathbf{G}\rvert}\sum_{R\in\mathbf{G}}P_R\mathbf{D}^i(R)_{ts}^*\exp(-im\alpha)\sum_nC_{nm}\exp(-in\gamma)d^l(\beta)Y^n_l(\theta,\phi)\]这里的求和$R$需要对所有的点群元素进行.
晶体点群symmetry-adapted function
首先给出32个点群对应的特征标表
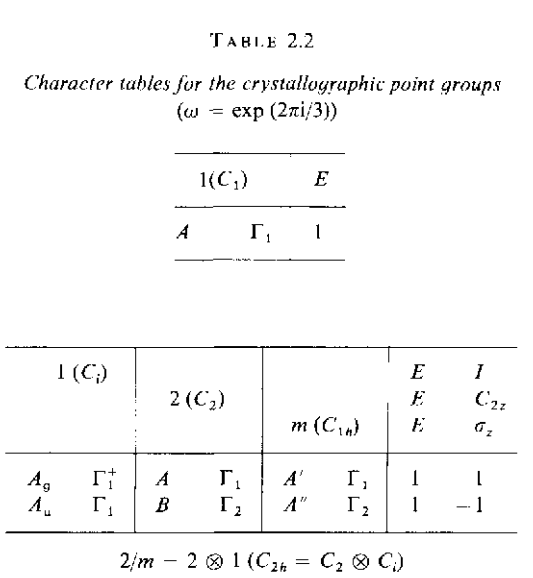



这个表中,几列表示的是点群的标记和其对应不可约表示的记法,这里同时给出了两种不同的标记方式,最后一列给出的就是点群的乘法表,这里需要说明的是,可能有的点群其乘法表示相同的,这也就是表中最后一列中会同时有两行不同的群元,他们分别代表的是不同点群的操作元,但是又具有相同的乘法表.在上表中,$i=1,2,3;j=1,2,3,4$是一些约定的符号记法.
晶体场劈裂
在孤立的环境中,电子周围的势场是个球对称的,在不考虑自旋的时候,其满足O(3)群对称性$\mathcal{D}^l{R(\alpha,\beta,\gamma)}$,这里的$l$是个整数,其实也就是实际中的角动量(暂时这么理解),$\mathcal{D}^l{R(\alpha,\beta,\gamma)}$的简并度是$(2l+1)$,它的基函数可以构成一个矢量,这$(2l+1)$个基函数对应的就是球谐函数$Y_l^m(\theta,\phi)(-l\le m\le l)$,因此这些波函数对应的能量此时都是相同的.当电子的环境发生改变的时候,也就是把它放到空间群中,那么其对称性就会从$O(3)$变成点群$\mathbf{G}$,原本的$(2l+1)$个简并能级就会发生劈裂,这些劈裂的能级就会用群$\mathbf{G}$的不可约表示来标记,下面给出$O(3)$群和点群的相容性关系
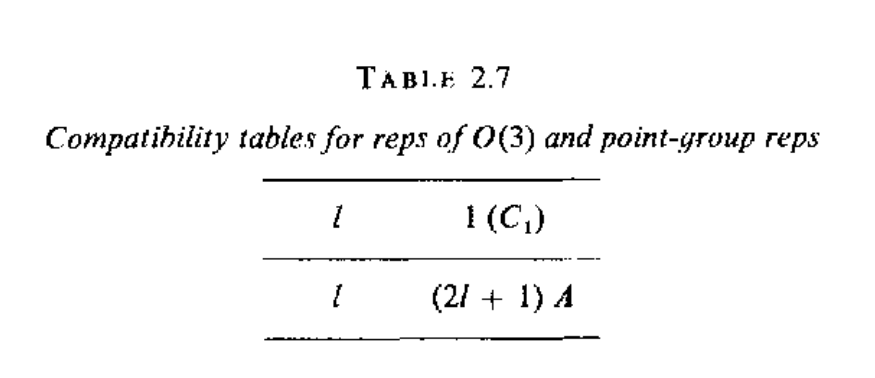

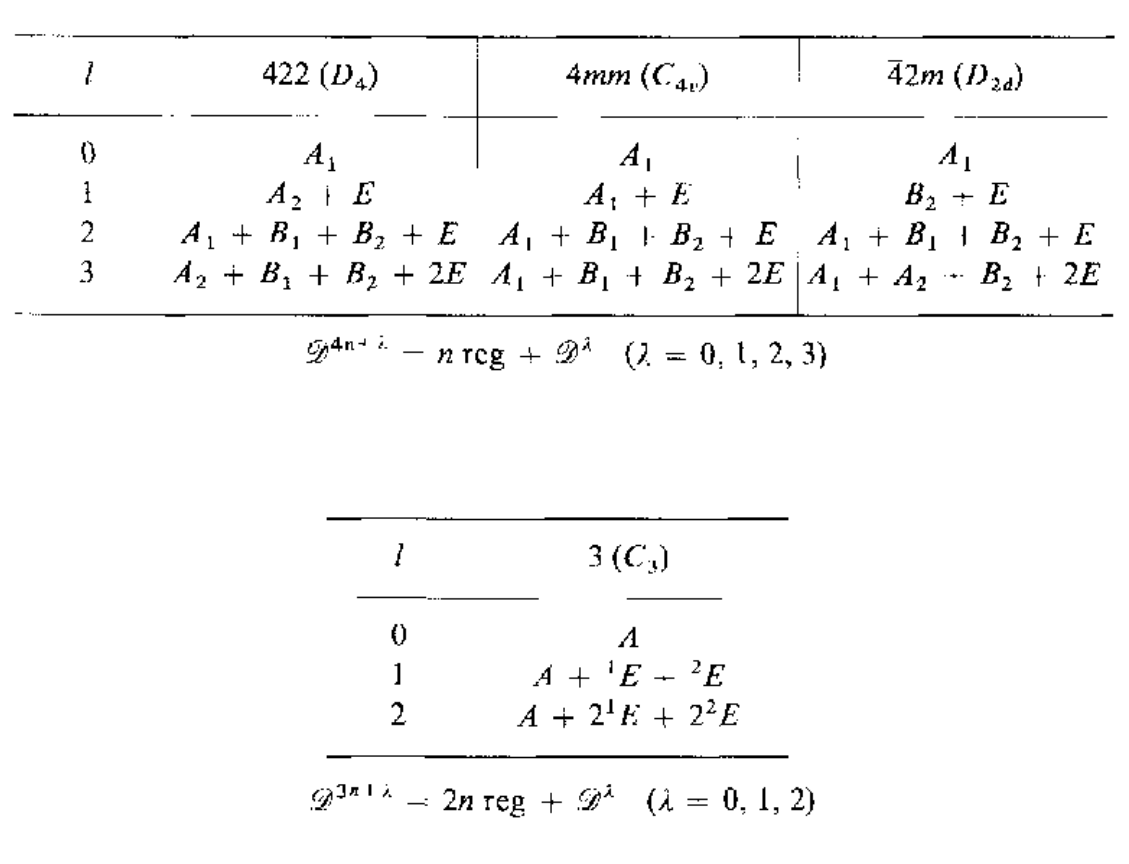
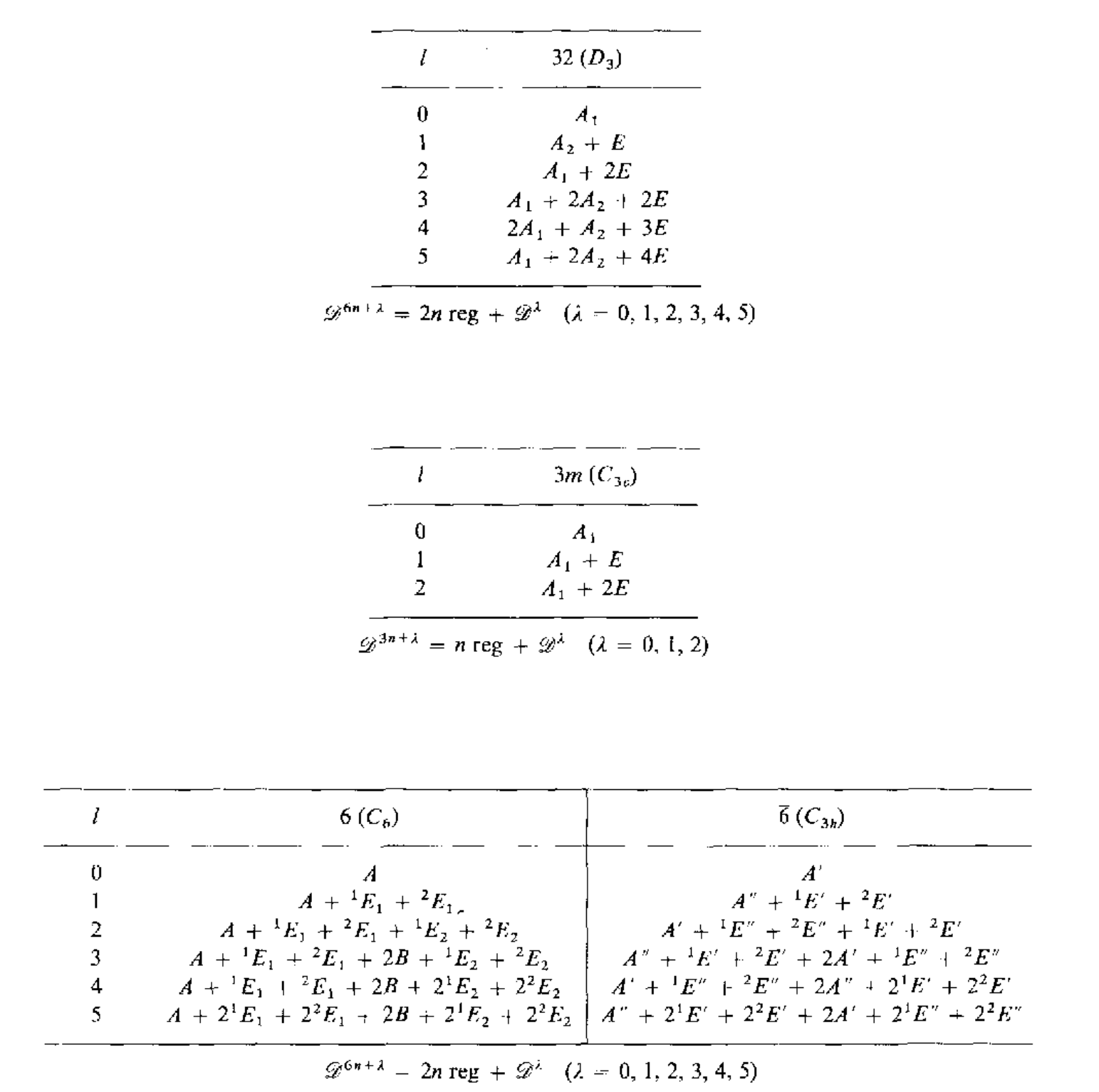
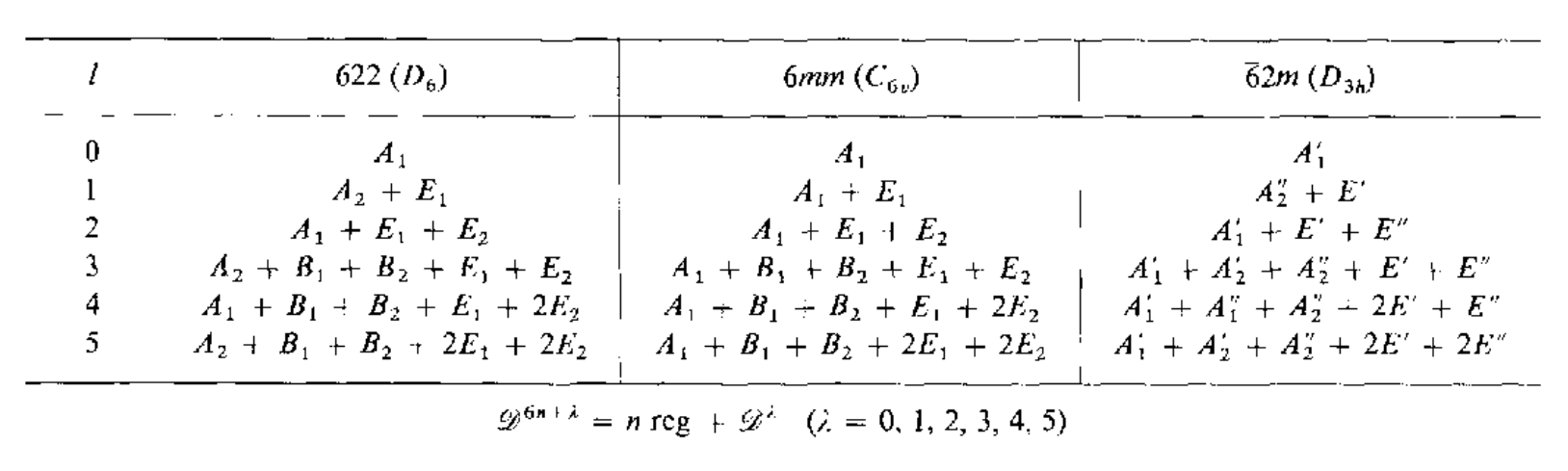


考虑将一个$l=2$的放置到$mm2(C_{2v})$点群中,根据下表
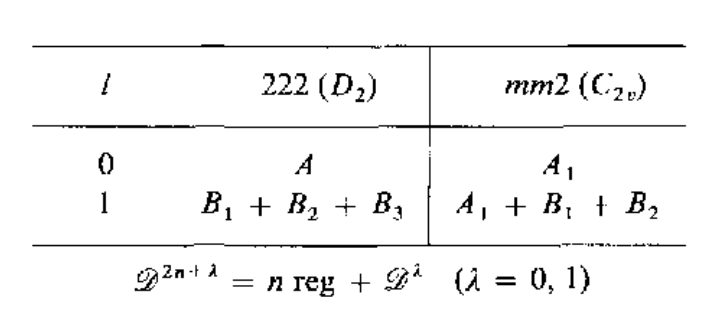
$l=2$的基函数为${Y_2^{-2}(\theta,\phi),Y_2^{-1}(\theta,\phi),Y_2^{0}(\theta,\phi),Y_2^{1}(\theta,\phi),Y_2^{2}(\theta,\phi)}$,根据下表
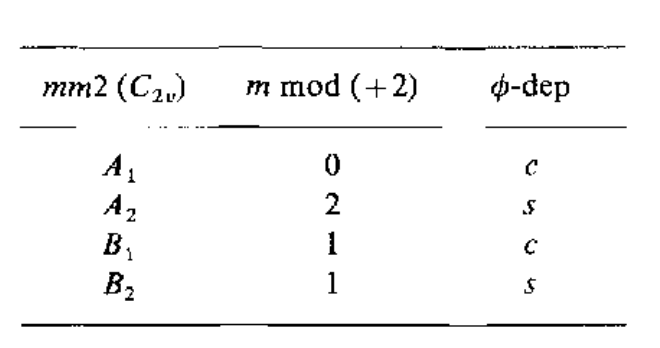
可以得到
\[A_1:Y_2^{0}(\theta,\phi),Y_2^{2,c}(\theta,\phi)\quad A_2:Y_2^{2,s}(\theta,\phi)\quad B_1:Y_2^{1,c}(\theta,\phi)\quad B_2:Y_2^{1,s}(\theta,\phi)\]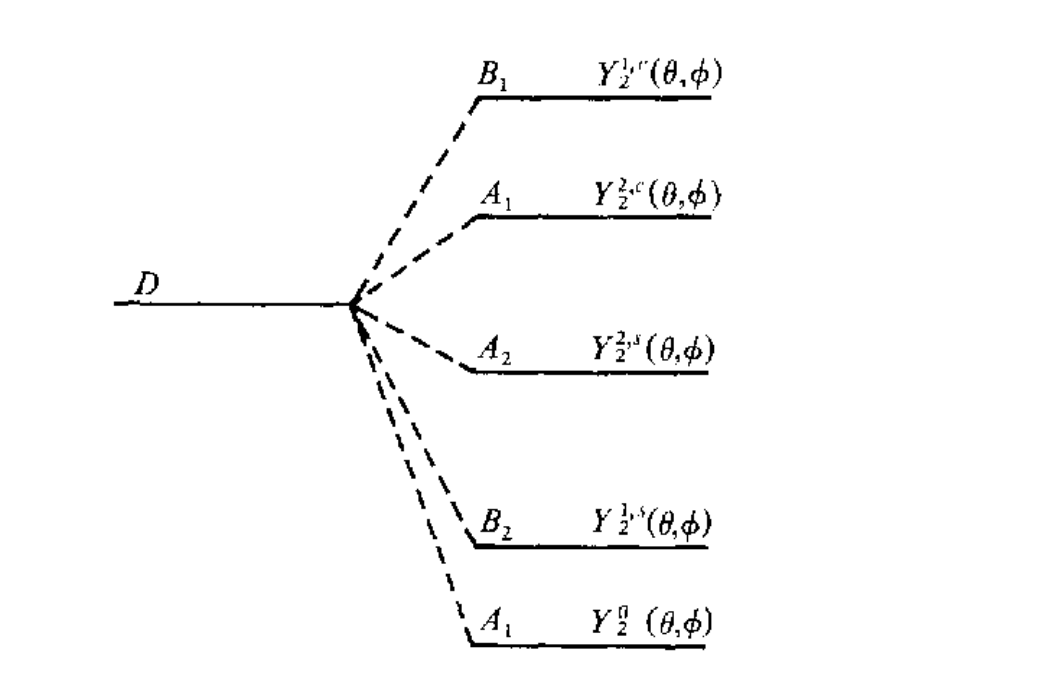
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |