虽然一直在利用2D和3D拓扑绝缘体的模型来进行一些研究，但是对这个模型的来源和对称性却并不明白是为什么，这里就来完整的整理一下到底这个模型是如何得到的，以及对应的对称性又是如何表示的。

对称性分析

Model Hamiltonian for topological insulators这篇文章中就是对模型的详细分析，博客的主要内容也是来源于这篇文章，主要是以Bi$_2$Se$_3$作为主要材料来得到3D拓扑绝缘体的模型，首先来看这个晶体的模型， png

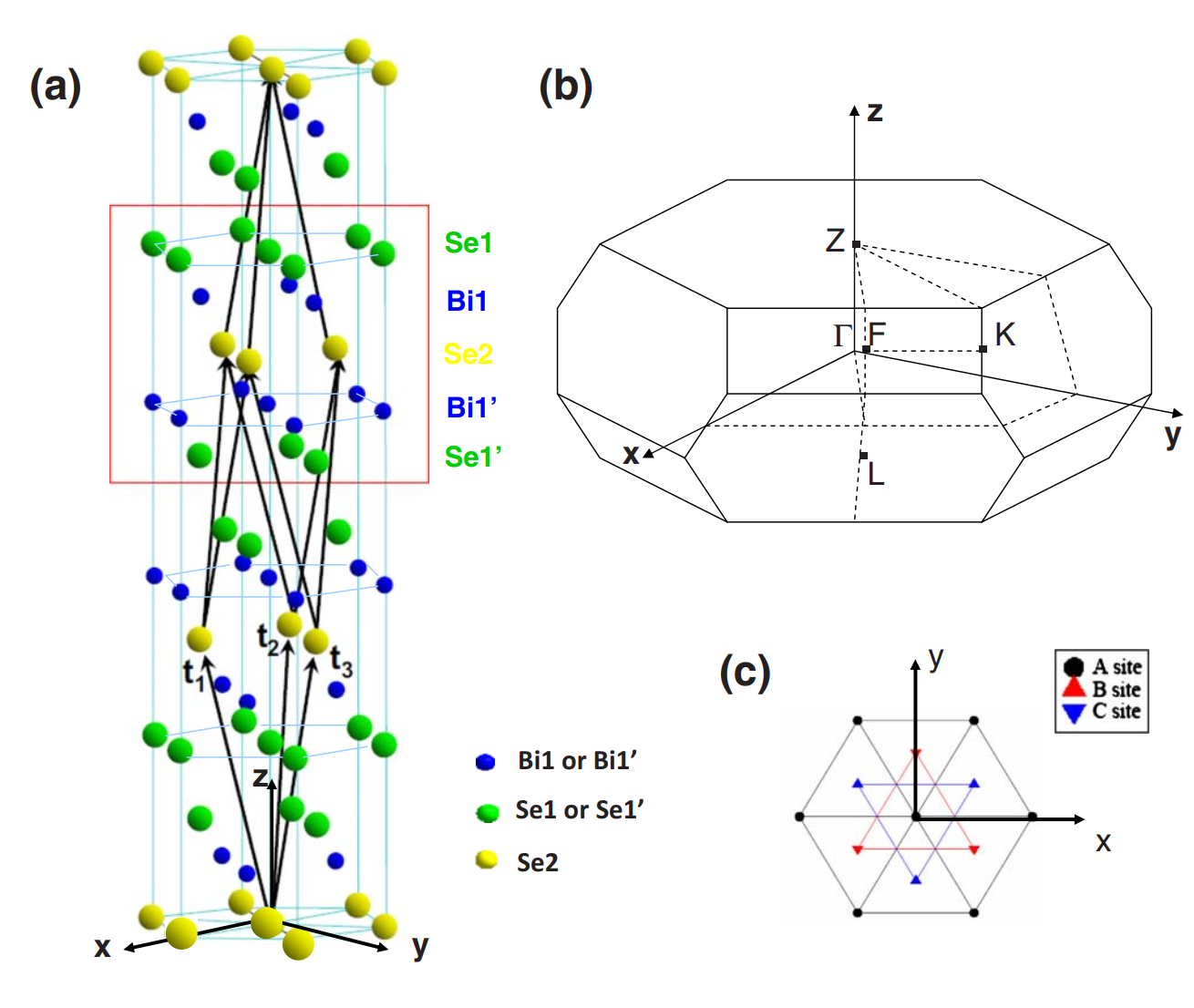
这个晶体结构具有如下对称性

$R^z_3$

\[x\rightarrow x\cos\theta-y\sin\theta,y\rightarrow x\sin\theta+y\cos\theta,z\rightarrow z\]

$R_2^x$

Se2$\rightarrow$Se2,Bi1$\rightarrow$Bi1$^{‘}$,Se1$\rightarrow$Se1$^{‘}$,$z\rightarrow -z,y\rightarrow -y,x\rightarrow x$，从这个对称操作可以看出Bi1(Se1)与Bi1$^{‘}$(Se1$^{‘}$)所在的层交换了位置

Inversion $\mathcal{P}$

Se2$\rightarrow$Se2,Bi1$\rightarrow$Bi1$^{‘}$,Se1$\rightarrow$Se1$^{‘}$,$z\rightarrow -z,x\rightarrow -x,y\rightarrow-y$,这里的反演操作是以Se2原子为反演中心，Bi1(Se1)与Bi1$^{‘}$(Se1$^{‘}$)所在的交换了位置。

Time reversal $\mathcal{T}$ 在spinfull的系统中，时间反演对称操作的作用满足$c_\uparrow\rightarrow c_\downarrow,c_\downarrow\rightarrow -c_\uparrow$，时间反演算符通常表示为$\mathcal{T}=\Theta\mathcal{K},\Theta=i\sigma_2$，这里的$\mathcal{K}$ 是算符复共轭操作，这里的$\sigma_i$是自旋空间的Pauli矩阵。

无论模型是什么样的,在构建模型的时候,都是基于材料对应的能带结构,所以首先要先分析Bi$_2$Se$_3$的能带结构,其包含的原子为Bi和Se,对应的电子结构为6s$^2$6p$^3$与4s$^2$4p$^4$,它们最外层的电子都是p电子,所以这里就可以只关注p电子的贡献,忽略其他s电子的贡献.从Bi$_2$Se$_3$的晶体结构上可以看出,这是一个层状的结构,所以在一个层的结构中,原子之间的化学键是比较强的,而层与层之间的化学键相对而言就比较弱,层间的相互作用主要是范德华力相互作用,相比较于层内化学键而言,范德华力比较弱,所以这个时候就主要关注一个层内的信息就可以.(从这里就可以体会一下在分析问题的时候,如何抓住最重要的内容,而忽略一些次要的作用,尽量利用一个最简单的考虑,来抓住最重要的作用)

此时只考虑一个层状内的信息,结构图中的红色框所示,此时每个层状内包含5个原子,因为直观组p电子的贡献,所以每个p电子对应的轨道是$(p_x,p_y,p_z)$,因此每个层状结构内,首先会有15个轨道(此时暂时不考虑自旋),标记为$\rvert\Gamma,\alpha\rangle,\Gamma=Bi1,Bi1^{‘},Se1,Se2,Se1^{‘}$,从晶体结构中可以看到Se2原子处在5层状结构的中间,是夹在两层Bi原子中间的,而两个Se原子则是处在最外层的.所有的Se原子都被Bi原子层分离开来,所以此时系统中最强的作用就是Bi原子层和Se原子层之间的耦合作用,这个作用将会产生能级排斥的作用,将Bi原子的能级向上推形成新的态

\[\rvert Bi\alpha\rangle,\rvert Bi^{'}\alpha\rangle\]

而Se原子的能级会被向下推形成三个新的态

\[\rvert S_\alpha\rangle,\rvert S^{'}_\alpha\rangle,\rvert S0_\alpha\rangle\]

如下图所示

png

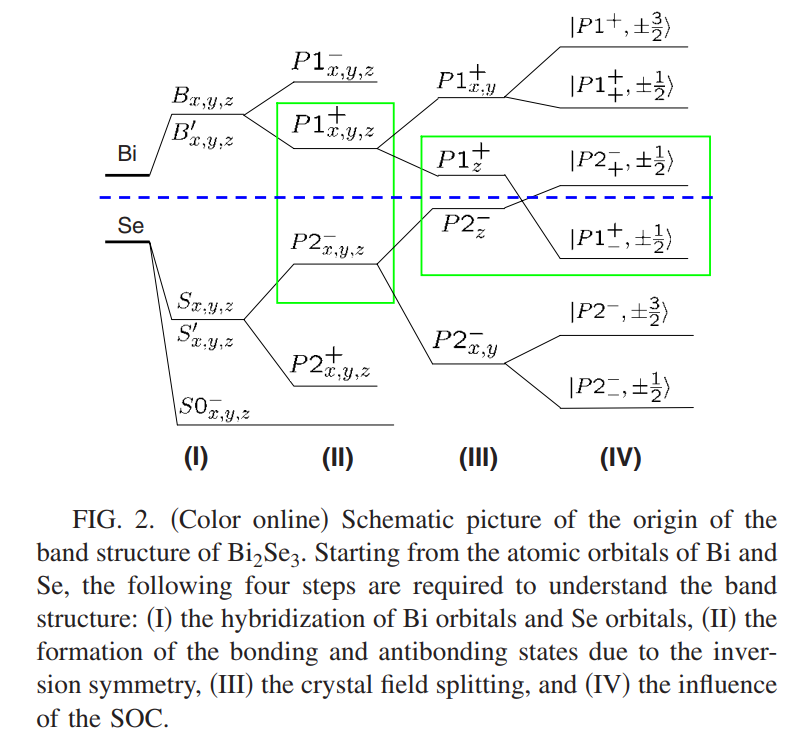
从前面的分析中知道,系统是具有反演对称性的,这里借用哈密顿量来理解体系具有对称性之后的性质,当系统具有某种对称性的时候,那么系统的哈密顿量就与这个对称性所表示的算符之间是满足对易关系的,那么说明这二者具有共同本征态,那么就可以利用反演对称性的本征值来标记体系哈密顿量所对应的能带进行标记,所以此时可以利用反演对称性对应的宇称来标记系统对应的能级,利用前面新的态来构成成键态与反键态,并利用反演对称性的将能带标用对应的宇称来标记

\[\begin{aligned} &\rvert P1^\pm,\alpha\rangle=\frac{1}{\sqrt{2}}(\rvert B_\alpha\rangle\mp\rvert B^{'}_\alpha\rangle)\\ &\rvert P2^\pm,\alpha\rangle=\frac{1}{\sqrt{2}}(\rvert S_\alpha\rangle\mp\rvert S^{'}_\alpha\rangle) \end{aligned}\]

这里的$\alpha=p_x,p_y,p_z$,当考虑了$\rvert B_\alpha(S_\alpha)\rangle$和$\rvert B_\alpha^{‘}(S_\alpha)^{‘}\rangle$之间的耦合之后,成键态和反键态对应的能量是不同的,会产生能级劈裂,反键态对应的能量会更高,而成键态对应的能量会降低,如图2(II)所示,在固体物理中,通常费米面附近的信息是最重要的,所以此时关注的能级主要是$\rvert P1^+,\alpha\rangle,\rvert P2^{-},\alpha\rangle,\alpha=p_x,p_y,p_z$,因此晶体是个层状结构,所以z方向和x,y方向是不同的,对应的能量也是不同的,所以$P1^+,p2^{-}$对应的$p_z$的能量与$p_x,p_y$的能量是不同的,此时$\rvert P1^+,p_{x,y}\rangle$对应的能量要高于$\rvert P1^+,p_{z}\rangle$,而$\rvert P2^{-},p_{x,y}\rangle$则是低于$\rvert P1^{-},p_{z}\rangle$,同样当关注费米面附近的能级的时候,此时导带主要是$\rvert P1^+,p_{z}\rangle$贡献的,而价带则主要是$\rvert P1^{-},p_{z}\rangle$贡献的,如图2(III)所示.

考虑SOC

当考虑自旋之后,上面的能级都是双重简并的,表示为$\rvert P1^+,\alpha,\sigma\rangle,\rvert P2^{-},\alpha,\sigma\rangle,\sigma=(\uparrow,\downarrow)$,此时再来考虑SOC效应,此时将原来的$p_x,p_y$轨道变换成$p_\pm$轨道来方便计算

\[\begin{aligned} &\rvert\Gamma,\alpha,p_{+}=-\frac{1}{\sqrt{2}}(\rvert\Gamma,p_x,\sigma\rangle-i\rvert\Gamma,p_y,\sigma\rangle)\\ &\rvert\Gamma,\alpha,p_{-}=\frac{1}{\sqrt{2}}(\rvert\Gamma,p_x,\sigma\rangle-i\rvert\Gamma,p_y,\sigma\rangle),\quad\Gamma=P1^+,P2^{-} \end{aligned}\]

当考虑SOC之后,原子对应的哈密顿量为$\hat{H}_{soc}=\lambda{\bf s\cdot L}$,此时有

\[\langle\Gamma,p_z,\uparrow(\downarrow)\rvert H_{soc}\rvert\Gamma,p_z,\uparrow(\downarrow)\rangle=0\]

可以看到这里z方向总的角动量是守恒的,在考虑了SOC之后标记一些新的态

\[\begin{aligned} &\rvert\Gamma,\frac{3}{2}\rangle=\rvert\Gamma,p_+,\uparrow\frac{1}{2}\rangle\quad\rvert\Gamma,\frac{3}{2}\rangle=\rvert\Gamma,p_+,\downarrow\rangle\\ &\rvert\Gamma_+,\frac{1}{2}\rangle=u_+^\Gamma\rvert\Gamma,p_z,\uparrow+v_+^\Gamma\rvert\Gamma,p_+,\downarrow\rangle\quad \rvert\Gamma_{-},\frac{1}{2}\rangle=u_{-}^\Gamma\rvert\Gamma,p_z,\uparrow+v_{-}^\Gamma\rvert\Gamma,p_+,\downarrow\rangle\\ &\rvert\Gamma_+,-\frac{1}{2}\rangle=(u_+^\Gamma)^{*}\rvert\Gamma,p_z,\downarrow+(v_+^\Gamma)^{*}\rvert\Gamma,p_+,\uparrow\rangle\quad \rvert\Gamma_{-},-\frac{1}{2}\rangle=(u_{-}^\Gamma)^{*}\rvert\Gamma,p_z,\downarrow+(v_{-}^\Gamma)^{*}\rvert\Gamma,p_{-},\uparrow\rangle \end{aligned}\]

当考虑了SOC之后可以看到$\rvert\Gamma,p_z,\uparrow\rangle(\rvert\Gamma,p_z,\downarrow\rangle)$和$\rvert\Gamma,p_{+},\downarrow\rangle(\rvert\Gamma,p_{-},\uparrow\rangle)$在SOC作用下耦合产生新的态,从而会产生能级排斥,最终

\[\rvert P1_{-}^{+},\pm\frac{1}{2}\rangle\]

被推向上

\[\rvert P2_{+}^{-},\pm\frac{1}{2}\rangle\]

被推向下,最终就会产生两个态之间的交叉,如图2(IV)所示.

模型构建

Bi$_2$Se$_3$能带计算结果如下图所示

png

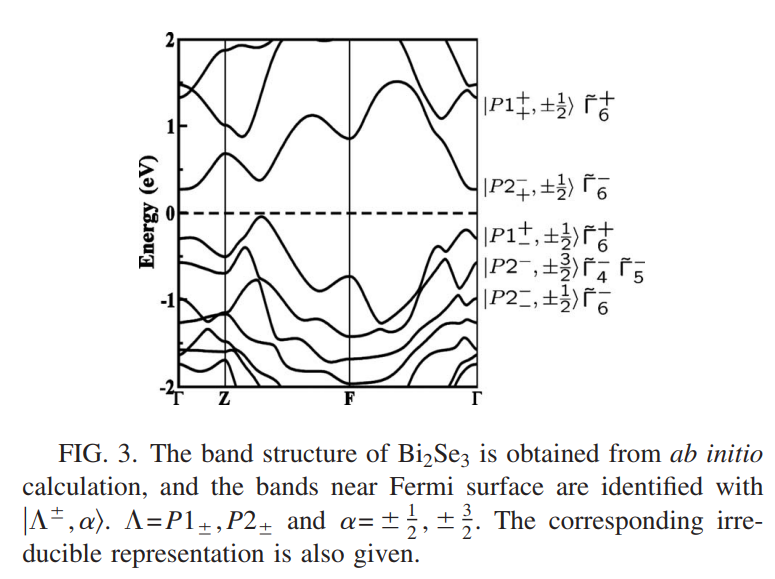
将费米面附近的能带标记为

$\rvert\Lambda^\pm,\alpha\rangle,\Gamma=P1\pm,P2\pm,\alpha=\pm\frac{1}{2},\pm\frac{3}{2}$$

Bi$2$Se$_3$对应的点群为$D^5{3d}$,其对应的特征标表为

png

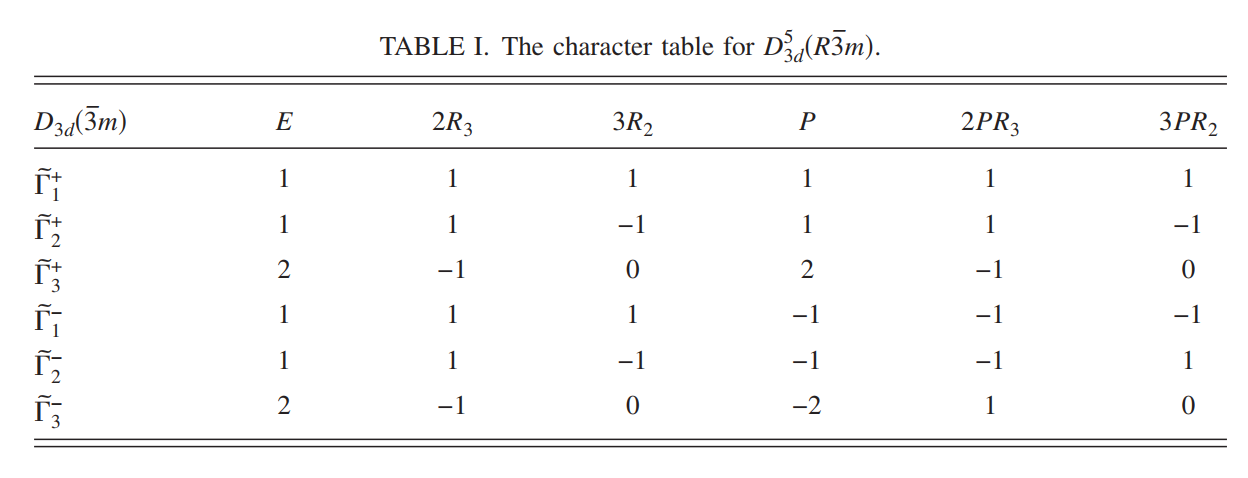
前面已经以及到晶体是具有反演对称性的,所以每个表示都具有一个确定的宇称，从Table I中可以看到，对于每个宇称，都有两个一维的表示

$\tilde{\Gamma}_1^\pm,\tilde{\Gamma}_2^\pm$$

和一个两维表示

$\tilde{\Gamma}_3^\pm$$

这里的上标代表着表示的宇称，可以采用最简单的原子轨道来构建波函数，已知$D_{3d}^5$点群的生成元为$R_3^z,R_2^x,\mathcal{P}$，可以根据对称操作对原胞中原子的作用，从而来确定这些操作对原子所贡献的轨道态的影响，首先可以看到$R_2^x$操作不会改变$p_x$轨道，但它会交换Bi1(Se1)和Bi$^{‘}$(Se$^{‘}$)的位置，也就对应着

\[\rvert B\rangle\rightarrow\rvert B^{'}\rangle\]

因此可以得到

\[R_2^x\rvert P1^+,p_x\rangle=-\rvert P1^+,p_x\rangle\]

利用相似的方法，同样可以得到点群生成元对其它态的变换作用

三重旋转$R_3^z$

\[\begin{aligned} &R_3^z\rvert \Lambda^\pm,p_x\rangle=\cos\theta\rvert\Lambda^\pm,p_x\rangle-\sin\theta\rvert\Lambda^\pm,p_y\rangle\\ &R_3^z\rvert \Lambda^\pm,p_y\rangle=\sin\theta\rvert\Lambda^\pm,p_x\rangle+\cos\theta\rvert\Lambda^\pm,p_y\rangle\\ &R_3^z\rvert\Lambda^\pm,p_z\rangle=\rvert\Lambda^\pm,p_z\rangle\quad\theta=\frac{2\pi}{3} \end{aligned}\]

两重旋转$R_2^x$

\[\begin{aligned} &R_2^x\rvert\Lambda^\pm,p_x\rangle=\mp\rvert\Lambda^\pm,p_x\rangle\\ &R_2^x\rvert\Lambda^\pm,p_y\rangle=\pm\rvert\Lambda^\pm,p_y\rangle\\ &R_2^x\rvert\Lambda^\pm,p_z\rangle=\pm\rvert\Lambda^\pm,p_z\rangle\\ \end{aligned}\]

反演操作$\mathcal{P}$

\[\mathcal{P}\rvert\Lambda^\pm,\alpha\rangle=\pm\rvert\Gamma6\pm,\alpha\rangle,\quad\alpha=p_x,p_y,p_z\]

上面的

\[\Gamma=P1_\pm,P2_\pm\]

从上面的变换关系，再结合Table I中点群$D_{3d}^5$的特征标表，可以对应得到

\[\rvert\Lambda^{+(-)},p_x\rangle,\rvert\Lambda^{+(-)},p_y\rangle\]

属于

\[\tilde{\Gamma}_3^{+(-)}\]

这个不可约表示，而

\[\rvert\Lambda^+,p_z\rangle\]

属于

\[\tilde{\Gamma}_1^+\]

这个表示

\[\rvert\Lambda^{-},p_z\rangle\]

属于

\[\tilde{\Gamma}_2^{-}\]

这个表示。要想确定某个态属于哪一个表示，方法如下：在上面已经确定了每个态在点群生成元下面的变换性质，也就可以得到这些操作对应的矩阵形式，那么自然就可以得到矩阵的trace，将其与特征标表进行对应，就可以得到每个态属于哪一个表示。

当需要考虑自旋之后，就需要在点群的单值表示基础上引入双群表示，其实也就是引入自旋表示

$\tilde{\Gamma}_6^+$$

当转动$2\pi$之后它会改变符号$+\rightarrow -$，最终可以得到$D_{3d}^5$的双值表示

png

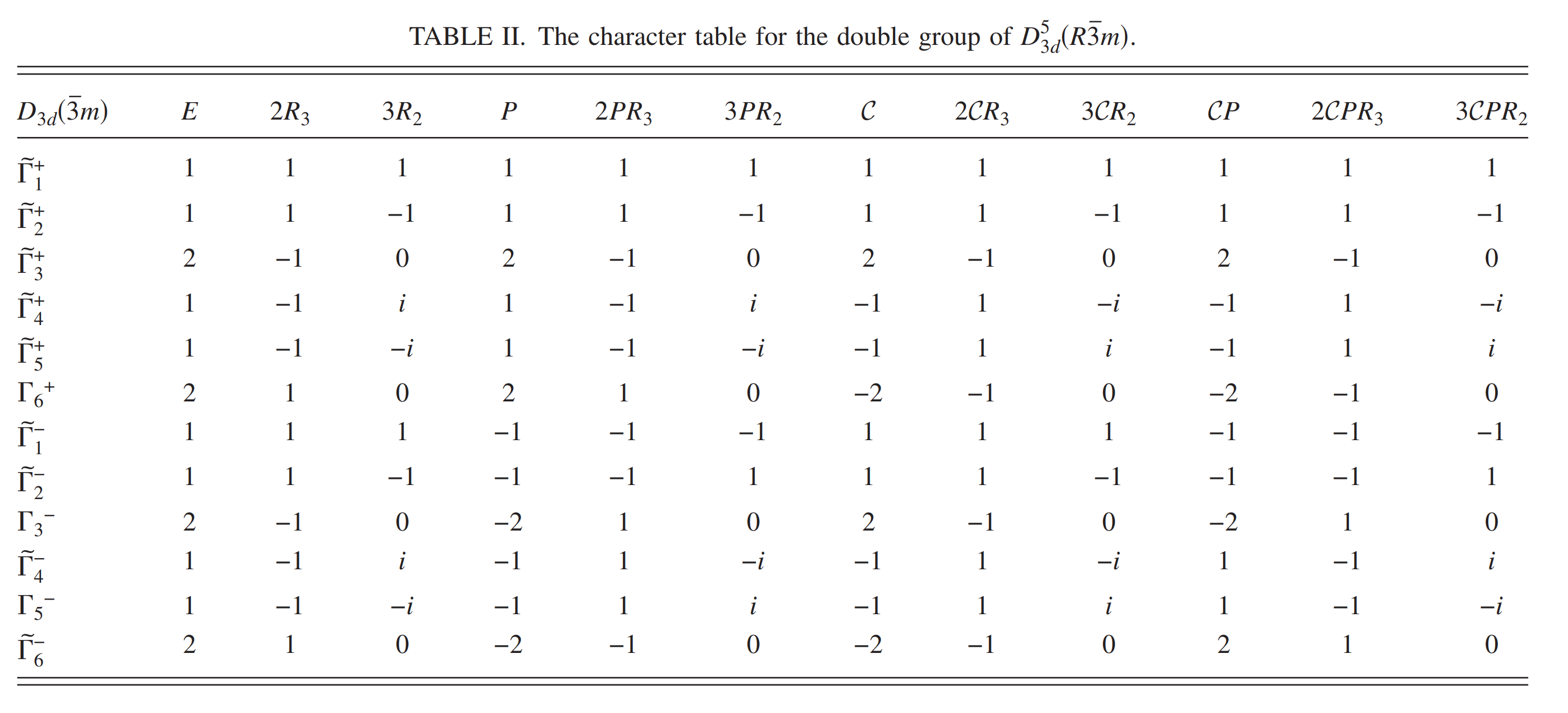
关于具体双值表示的推导，可以参考文章Model Hamiltonian for topological insulators中的附录，这里直接翻译一下文章中的内容，

png

从上面的关系中可以看到

$\tilde{\Gamma}6^\pm$与$\tilde{\Gamma}{1,2}^\pm$$

的直积仍然是$\tilde{\Gamma}_6^\pm$，所以

\[\rvert\Lambda^+,\pm\frac{1}{2}\rangle\]

属于

\[\tilde{\Gamma}_6^{+}\]

表示，而

\[\rvert\Lambda^{-},\pm\frac{1}{2}\rangle\]

属于

\[\tilde{\Gamma}_6^{-}\]

表示，而态

\[\rvert\Lambda^{-},\pm\frac{3}{2}\rangle\]

是来自于

\[\rvert\Lambda,p_{x,y}\rangle\]

与自旋的组合，根据上面的结果可以得到

\[\rvert\Lambda^\pm,\pm\frac{3}{2}\rangle\]

应该属于

\[\tilde{\Gamma}_4^\pm\]

和

\[\tilde{\Gamma}_5^\pm\]

的组合，将

\[\rvert\Lambda^\pm,\pm\frac{3}{2}\rangle\]

这两个态进行组合可以得到

\[\begin{aligned} &\rvert\Lambda^\pm,\tilde{\Gamma}_4\rangle\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,\frac{3}{2}\rangle+\rvert\Lambda^\pm,-\frac{3}{2}\rangle)\in\tilde{\Gamma}_4^\pm\\ &\rvert\Lambda^\pm,\tilde{\Gamma}_5\rangle\frac{1}{\sqrt{2}}(\rvert\Lambda^\pm,\frac{3}{2}\rangle-\rvert\Lambda^\pm,-\frac{3}{2}\rangle)\in\tilde{\Gamma}_5^\pm\\ \end{aligned}\]

那么在双值表示下，这些态在群生成元的操作下满足下列关系

三重旋转$R_3^z$

\[R_3^z\rvert\Lambda,\pm\frac{1}{2}\rangle=e^{\pm i\pi/3}\rvert\Lambda,\pm\frac{1}{2}\rangle\quad R_3^z\rvert\Lambda,\pm\frac{3}{2}\rangle=\pm\rvert\Lambda,\pm\frac{3}{2}\rangle\quad\Lambda=P1_\pm^\pm,P2_\pm^\pm\]

二重旋转$R_2^x$

\[\begin{aligned} & R_2^x\rvert\Lambda^+,\pm\frac{1}{2}\rangle=i\rvert\Lambda^+,\mp\frac{1}{2}\rangle\quad R_2^x\rvert\Lambda^-,\pm\frac{1}{2}\rangle=-i\rvert\Lambda^-,\mp\frac{1}{2}\rangle\\ & R_2^x\rvert\Lambda^+,\pm\frac{3}{2}\rangle=i\rvert\Lambda^+,\mp\frac{3}{2}\rangle\quad R_2^x\rvert\Lambda^-,\pm\frac{3}{2}\rangle=-i\rvert\Lambda^-,\mp\frac{3}{2}\rangle \end{aligned}\]

反演对称$\mathcal{P}$

\[\mathcal{P}\rvert\Lambda^\pm,\alpha\rangle\quad\Lambda=P1_\pm,P2_\pm\quad\alpha=\pm\frac{3}{2},\pm\frac{1}{2}\]

通过上面的分析，就得到了在考虑SOC下，这些态在晶体点群对称操作下的变换性质，从而也就可以得到这些态所属的表示，Bi$_2$Se$_3$的能带计算及能带表示如下所示

png

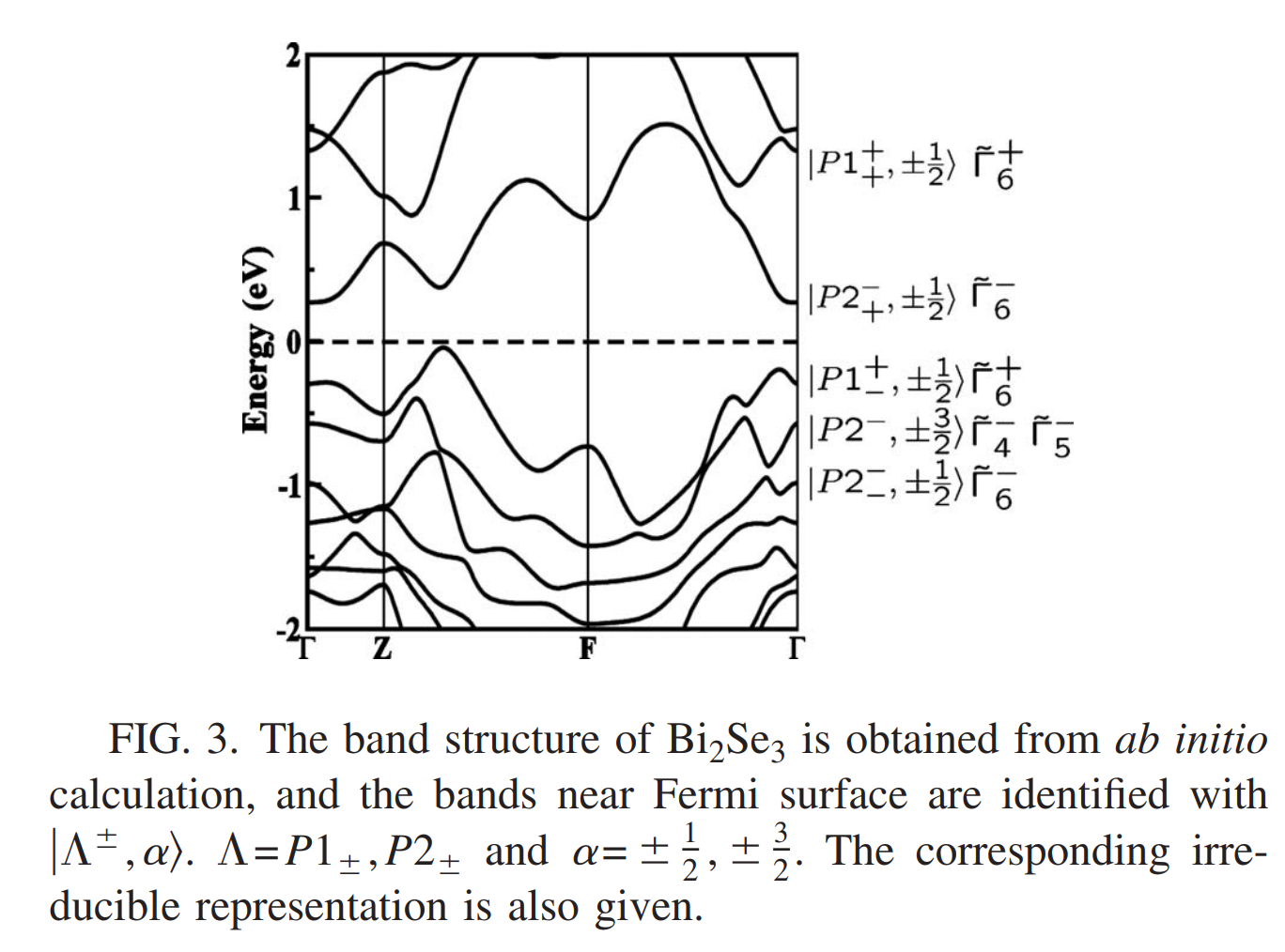
下面就来推导如何用一个哈密顿量来描述Bi$_2$Se$_3$在$\Gamma$点处的低能物理性质，首先可以看到在费米面附近导带和价带主要是由

\[\rvert P1_{-}^{+},\pm\frac{1}{2}\rangle,\rvert P2_{+}^{-},\pm\frac{1}{2}\rangle\]

这四个态决定，且分别属于 $\tilde{\Gamma}_6^+,\tilde{\Gamma}_6^{-}$ 这两个不可约表示，这里因为主要考虑的就是四个态，所以就可以将低能附近的哈密顿量用$4\times 4$的矩阵表示出来，通常$4\times 4$的哈密顿量都会用Dirac矩阵来展开

\[\begin{aligned} &\hat{H}_\text{eff}=\epsilon(\mathbf{k})I+\sum_id_i(\mathbf{k})\Gamma_i+\sum_{ij}d_{ij}(\mathbf{k})\Gamma_{ij}\\ &\{\Gamma_i,\Gamma_j\}=2\delta_{ij}\quad \Gamma_{ij}=\frac{1}{2i}[\Gamma_i,\Gamma_j] \end{aligned}\]

这里的$d_i(\mathbf{k}),d_{ij}(\mathbf{k})$是对应的一些系数。

这里做一些说明，到这里只是知道了哈密顿量描写的是费米能级附近四个态对应的一个有效的低能哈密顿量，所以其对应的维度就是4，通常$4\times 4$的哈密顿量习惯使用Dirac矩阵来展开，因为其满足的一些性质可以很好的来进行物理性质分析和研究，所以这也就是为什么通常见到的哈密顿量都是用Dirac矩阵或者Pauli矩阵为基矢进行展开的，但是这里只是完成了第一步，将哈密顿量的抽象形式表示了出来，而其前面的系数以及满足的对称性对应的矩阵形式，此时仍然是不知道的，这就需要在确定了写出这个$4\times 4$哈密顿量的基矢是什么，在确定之后才能得到这些具体的内容。

前面已将知道了，在费米面附近主要关注的是

\[\rvert P1_{-}^{+},\pm\frac{1}{2}\rangle,\rvert P2_{+}^{-},\pm\frac{1}{2}\rangle\]

这四个态，那么就将低能哈密顿量的基矢选择为

\[{\color{blue}\rvert P1_{-}^{+},\frac{1}{2}\rangle\quad \rvert P2_{+}^{-},\frac{1}{2}\rangle\quad \rvert P1_{-}^{+},-\frac{1}{2}\rangle\quad \rvert P2_{+}^{-},-\frac{1}{2}\rangle}\label{eq1}\]

在前面也已经知道了在双值表示这四个态在对称操作下的变换，那么就可以得到这些变换操作的具体矩阵形式,这里以反演对称$\mathcal{P}$为例,构建在上面的基矢下面如何将反演对称操作表示成矩阵形式,从前面的分析知道,反对称操作满足

\[\mathcal{P}\rvert\Lambda^\pm,\alpha\rangle\quad\Lambda=P1_\pm,P2_\pm\quad\alpha=\pm\frac{3}{2},\pm\frac{1}{2}\]

所以在基矢(\ref{eq1})下面可以看到,反演操作不会影响自旋,对于宇称为$+$的那么就得到$+$,反之对于宇称为$-$的态,得到的就是$-$,将反演对称操作表示在这个基矢下面可以得到

\[P=\sigma_0\otimes\tau_z\]

这里的$\sigma$是作用在基矢的自旋自由度上,而$\tau$则是作用在轨道自由度上,基矢排列的顺序对应的矩阵直积顺序为$\sigma_i\otimes\tau_j$,通常在理论文章中看到会将哈密顿量的基矢表示为

\[\Psi_\mathbf{k}=(c_{a\mathbf{k},\uparrow},c_{b\mathbf{k},\uparrow},c_{a\mathbf{k},\downarrow},c_{a\mathbf{k},\downarrow})\label{eq2}\]

将基矢表示方向(\ref{eq1})和(\ref{eq2})进行比较可以看到,这里的$a,b$轨道对应的宇称是相反的.

在基矢(\ref{eq1})的表示下,时间反演操作为

\[\mathcal{T}=i\sigma_2\otimes\tau_0\mathcal{K}\quad\mathcal{K}\rightarrow\text{复共轭}\]

三重转动操作$R_3^z$为

\[R_3^z=e^{i\frac{\sigma_3\otimes\tau_0}{2}\theta}\quad\theta=\frac{2\pi}{3}\]

两重转动操作$R_2^x$

\[R_2^x=i\sigma_x\otimes\tau_z\]

到这里之后,首先就明确了哈密顿量的基矢,那么也就知道了前面的在写出低能哈密顿量时Dirac矩阵的基矢,而根据上面得到的在这些基矢下面得到的对称操作的矩阵表示,利用这些对称操作的表示对Dirac矩阵进行操作,那么就可以知道这些Dirac矩阵是属于双群的哪一个表示,如下图所示

png

因为哈密顿量在这些操作下是不变的,这就要求Dirac矩阵前面的系数和Dirac矩阵是属于相同的不可约表示的,从Table III中就可以得到确定表示下的基矢,到这一步之后,剩下的就是将Dirac矩阵和与其属于相同表示的系数$d_i(\mathbf{k}),d_{ij}(\mathbf{k})$组合起来,比如$\Gamma_5$属于$\tilde{\Gamma}_1^{+}$这个表示,那么其前面的系数也应该属于$\tilde{\Gamma}_1^{+}$这个表示,所以对应的系数为${1,k_x^2+k_y^2,k_z^2}$,一般情况下这一项为

\[[M_0+M_1k_z^2+M_2(k_x^2+k_y^2)]\Gamma_5\]

利用这个方式,最终就可以得到完整的低能有效哈密顿量为

\[\begin{aligned} H_\text{eff}^{'}&=H_0^{'}+H_3^{'}\\ H_0^{'}&=\epsilon(\mathbf{k})+M(\mathbf{k})\Gamma_5+B(k_z)k_z\Gamma_4+A(k_\parallel)(k_y\Gamma_1-k_x\Gamma_2)\\ H_3^{'}&=R_1\Gamma_3(k_x^3-3k_xk_y^2)+R_2\Gamma_4(3k_x^2k_y-k_y^3)\\ \epsilon(\mathbf{k})&=C_0+C_1k_z^2+C_2k_\parallel^2\quad M(\mathbf{k})=M_0+M_1k_z^2+M_2k_\parallel^2\quad B(k_z)=B_0+B_2k_z^2\quad k_\parallel =k_x^2+k_y^2\label{eq3} \end{aligned}\]

到此就得到对应的低能有效哈密顿量,从而也得到了对应的对称性操作.