这里来重复Surface States of topological insulator这片文章中的一个推到，因为在学习边界态理论的过程中始终会提及到这篇文章，而且其中的内容对理解表面态还是很有启发意义的，所以这里整理一下
其中的一些推导。
{:.info}

$H=(c_{0}+c_{z}k_{z}^{2}+c_{\parallel}k_{\parallel}^{2})+(-m_{0}+m_{z}k_{z}^{2}+m_{\parallel}k_{\parallel}^{2})\tau_{z}+v_{z}k_{z}\tau_{y}+v_{\parallel}(k_{y}\sigma_{x}-k_{x}\sigma_{y})\tau_{x}$

在考虑具体问题的时候，通常线性项是最重要的（因为拓扑的边界态，主要是domain wall的物理，而这部分通常只需要线性阶的近似就可以抓住本质，而且在形式上也就是要对应Dirac方程），这里先忽略二次项和一些常数项

$H=-m_{0}\tau_{z}+v_{z}k_{z}\tau_{y}+v_{\parallel}(k_{y}\sigma_{x}-k_{x}\sigma_{y})\tau_{x}\label{eq1}$

这里对坐标系进行转动，通过观察哈密顿量可以发现每个$k_{i}$都会于一个矩阵相联系在一起

$k_{z}\tau_{y},\quad k_{y}\sigma_{x}\tau_{x},\quad k_{x}\sigma_{y}\tau_{x}$

当对坐标系进行转动之后，假设新的空间坐标为$(k_{1},k_{2},k_{3})$，那么它们也同样会与一组新的矩阵组合在一起，这里假设在这个转动下，$\tau_{i}\rightarrow S^{i}_{1},\sigma_{i}\rightarrow S^{i}_{2}$，在变换之后$S_{i}^{j}$同样需要满足下面的代数关系

$[S_{a}^{i},S_{b}^{j}]=2i\delta_{ab}\epsilon^{ijk}S_{a}^{k}\label{eq2}$

这里旋转转动轴为$y$轴，那么转动前后有$k_{y}=k_{2}$，唯一变化的就是$(k_{x},k_{z})\rightarrow(k_{1},k_{3})$。

png

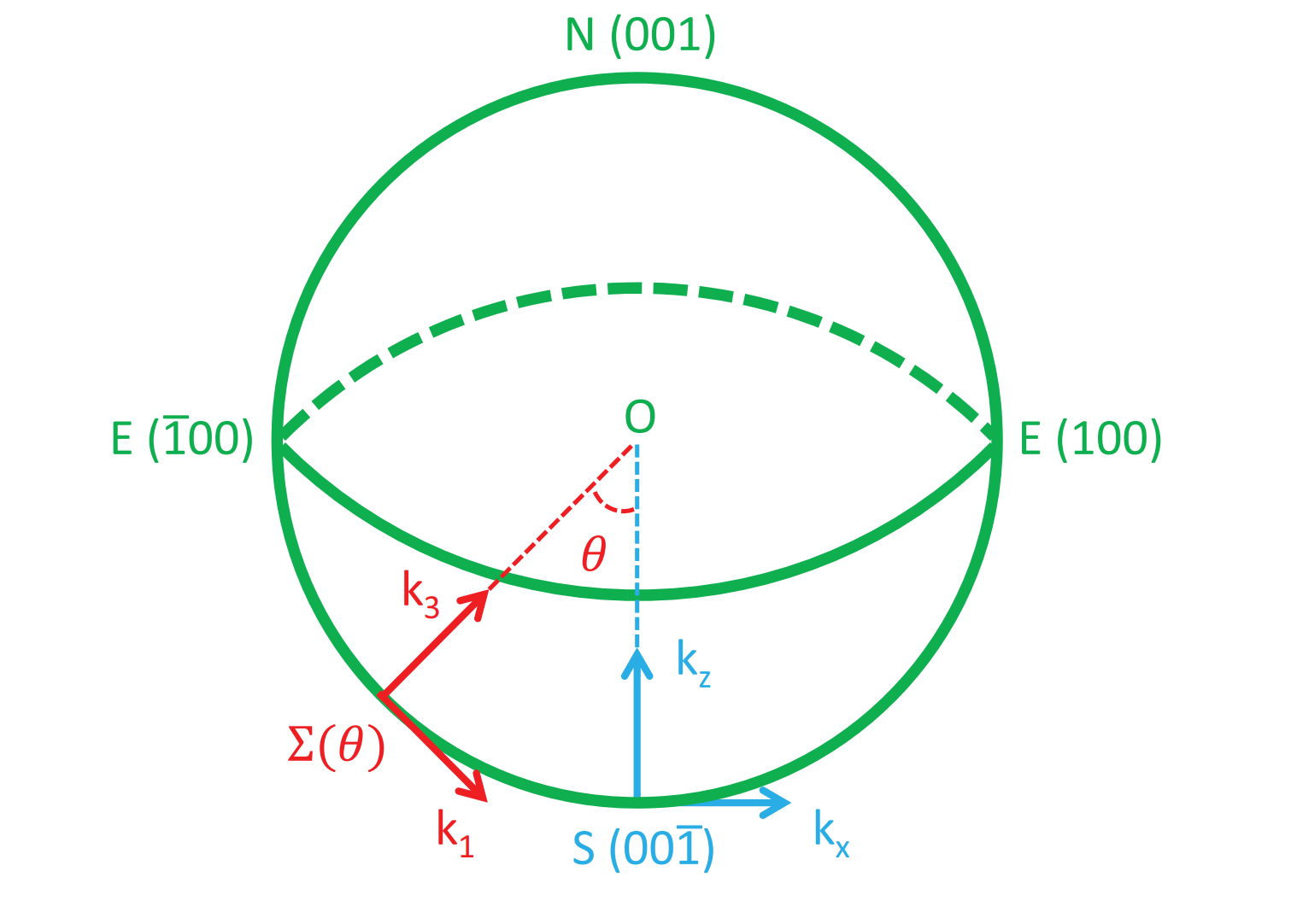
首先来观察哈密顿量(\ref{eq1})中可以看到，$\tau_{z}$只与一个常数项组合，及无论原来的$k_{x,y,z}$坐标轴怎样转动，可以选定在转动前后$S_{1}^{z}=\tau_{z}$。而且这里在转动的时候，选取的转动轴是$k_{y}$，那么可以再选定$\sigma$与$S_{2}^{y}$之间的对应关系$S_{2}^{y}=\sigma_{y}$，此时的这个选择是具有任意性的，同样你也可以选择$\sigma_{x}$或者$\sigma_{z}$，最终只需要这些$S_{2}^{i}$之间满足(\ref{eq2})这个关系即可。到现在为止，确定的关系为

$\begin{aligned} \mathbf{S}_{1}&=\{S_{1}^{x},S_{1}^{y},\tau_{z}\}\\ \mathbf{S}_{2}&=\{S_{2}^{x},\sigma_{y},S_{2}^{z}\}\\ \end{aligned}$

下面来确定剩下几个算符的形式，以$S_{1}^{x,y}$为例说明其选择的形式，最重要的就是满足(\ref{eq2})这个关系，所以可以将其形式选择为

$S_{1}^{x}=\alpha\tau_{x}+\beta\sigma_{y}\tau_{y},\quad S_{1}^{y}=\alpha\tau_{y}-\beta\sigma_{y}\tau_{x}$

这里再说明一下这个形式为什么这么选择，因为要满足(\ref{eq2})这个关系，首先$S_{1}^{x,y}$只能是$\tau_{x,y}$的线性组合的形式，而其次因为$\sigma_{y}$前面也说明了，它已经是选定的，所以这里同样可以将其认为是一个参数，这就是为什么要把$S_{2}^{x,y}$改写成这样的形式，这里强调的知识说形式，并不是说$S_{1}^{x}$就一定要写成$\alpha\tau_{x}+\beta\sigma_{y}\tau_{y}$，可以选择其它的组合形式，比如$S_{1}^{x}=\alpha\sigma_{y}\tau_{y}+\beta\tau_{x}$，只要满足(\ref{eq2})这个关系才是重点，而且这个条件就会进一步对$\alpha,\beta$作出限制要求，因为$(S_{i}^{j})^{2}=1$，所以可以得到

$\alpha^2+\beta^{2}=1$

与上面相同的逻辑，此时就可以将$S_{2}^{x,z}$的形式也给出一种选择

$S_{2}^{x}=\alpha\sigma_{x}-\beta\sigma_{z}\tau_{z},\quad S_{2}^{z}=\alpha\sigma_{z}+\beta\sigma_{x}\tau_{z}$

整理到一起即为

$\begin{aligned} \mathbf{S}_{1}&=\{\alpha\tau_{x}+\beta\sigma_{y}\tau_{y},\alpha\tau_{y}-\beta\sigma_{y}\tau_{x},\tau_{z}\}\\ \mathbf{S}_{2}&=\{\alpha\sigma_{x}-\beta\sigma_{z}\tau_{z},\sigma_{y},\alpha\sigma_{z}+\beta\sigma_{x}\tau_{z}\}\\ \end{aligned}\label{eq3}$

{\color{blue}这里的形式的选取，首先是要确定不变的$\tau_{z}$和$\sigma_{y}$，之后就是为了满足(\ref{eq2})进行的形式选取，这里存在极大的冗余自由度，因为最基本的要求是满足(\ref{eq2})，但是很显然，满足这个条件的并不只有现在这一种选择。}

通过(\ref{eq3})已经建立起来了$\vec{\tau}\rightarrow \mathbf{S}_{1}$以及$\vec{\sigma}\rightarrow \mathbf{S}_{2}$之间的关系，那么反过来同样可以将$\sigma_{i},\tau_{j}$表示为$S_{2}^{i},S_{1}^{j}$的形式，首先将(\ref{eq3})展开为方程形式

$\left\{ \begin{array}{c} \alpha\tau_{x}+\beta\sigma_{y}\tau_{y}=S_{1}^{x}\\ \alpha\tau_{y}-\beta\sigma_{y}\tau_{x}=S_{1}^{y}\\ \tau_{z}=S_{1}^{z}\\ \end{array} \right.\quad \left\{ \begin{array}{c} \alpha\sigma_{x}-\beta\sigma_{z}\tau_{z}=S_{2}^{x}\\ \sigma_{y}=S_{2}^{y}\\ \alpha\sigma_{z}+\beta\sigma_{x}\tau_{z}=S_{2}^{z} \end{array} \right.\label{eq4}$

通过求解(\ref{eq4})即可以得到

$\left\{ \begin{array}{c} \tau_{x}=\beta\sigma_{y} S_{1}^{y}-\alpha S_{1}^{x}\\ \tau_{y}=\beta\sigma_{y} S_{1}^{x}+\alpha S_{1}^{y}\\ \tau_{z}=S_{1}^{z}\\ \end{array} \right.\quad \left\{ \begin{array}{c} \sigma_{x}=\alpha S_{2}^{x}+\beta\tau_{z}S_{2}^{z}\\ \sigma_{y}=S_{2}^{y}\\ \sigma_{z}=\alpha S_{2}^{z}-\beta S_{2}^{x}\tau_{z} \end{array} \right.$ $\left\{ \begin{array}{c} \tau_{x}=\beta S_{2}^{y}S_{1}^{y}-\alpha S_{1}^{x}\\ \tau_{y}=\beta S_{2}^{y} S_{1}^{x}+\alpha S_{1}^{y}\\ \tau_{z}=S_{1}^{z}\\ \end{array} \right.\quad \left\{ \begin{array}{c} \sigma_{x}=\alpha S_{2}^{x}+\beta S_{1}^{z}S_{2}^{z}\\ \sigma_{y}=S_{2}^{y}\\ \sigma_{z}=\alpha S_{2}^{z}-\beta S_{2}^{x}S_{1}^{z} \end{array} \right.\label{eq5}$

这里利用欧拉转动，来描述坐标系基矢之间的变换关系，这里是以$y$轴为中心进行的转动，那么对应的欧拉转动矩阵为

$\left[ \begin{array}{ccc} \cos\theta&0&\sin\theta\\ 0&1&0\\ -\sin\theta&0&\cos\theta \end{array} \right]$

那么就可以得到转动前后两个坐标系之间的关系为

$\left\{ \begin{array}{c} k_{1}=k_{x}\cos\theta+k_{z}\sin\theta\\ k_{2}=k_{y}\\ k_{3}=k_{z}\cos\theta-k_{x}\sin\theta \end{array} \right.\quad\left\{ \begin{array}{c} k_{x}=k_{1}\cos\theta-k_{3}\sin\theta\\ k_{y}=k_{2}\\ k_{z}=k_{3}\cos\theta+k_{1}\sin\theta \end{array} \right.$

将$k_{x,y,z}\rightarrow k_{1,2,3}$并且利用(\ref{eq5})将下面的哈密顿量进行改写

$H=-m_{0}\tau_{z}+v_{z}k_{z}\tau_{y}+v_{\parallel}(k_{y}\sigma_{x}-k_{x}\sigma_{y})\tau_{x}$

分别将表达式进行替换

$-m_{0}\tau_{z}=-m_{0}S_{1}^{z}\label{eq6}$ $\begin{aligned} v_{z}k_{z}\tau_{y}&=v_{z}(k_{3}\cos\theta+k_{1}\sin\theta)(\beta S_{2}^{y} S_{1}^{x}+\alpha S_{1}^{y})\\ &=v_{z}(k_{3}\beta\cos\theta S_{2}^{y}S_{1}^{x}+k_{3}\alpha \cos\theta S_{1}^{y}+k_{1}\beta\sin\theta S_{2}^{y}S_{1}^{x}+k_{1}\alpha\sin\theta S_{1}^{y})\label{eq7} \end{aligned}$ $\begin{aligned} v_{\parallel}k_{y}\sigma_{x}\tau_{x}&=v_{\parallel}k_{2}(\alpha S_{2}^{x}+\beta S_{1}^{z}S_{2}^{z})(\beta S_{2}^{y}S_{1}^{y}-\alpha S_{1}^{x})\\ &=v_{\parallel}k_{2}(\alpha\beta S_{2}^{x}S_{2}^{y}S_{1}^{y}-\alpha^{2}S_{2}^{x}S_{1}^{x}+\beta^{2}S_{1}^{z}S_{2}^{z}S_{2}^{y}S_{1}^{y}-\alpha\beta S_{1}^{z}S_{2}^{z}S_{1}^{x})\\ &=v_{\parallel}k_{2}[\alpha\beta(S_{2}^{x}S_{2}^{y}S_{1}^{y}-S_{1}^{z}S_{2}^{z}S_{1}^{x})-(\alpha^{2}+\beta^{2})S_{2}^{x}S_{1}^{x}]\label{eq8} \end{aligned}$

在这一步的推导中使用了

$S_{1}^{z}S_{2}^{y}=-iS_{x}\quad S_{2}^{z}S_{2}^{y}=-S_{2}^{x}\quad S_{1}^{z}S_{2}^{y}S_{2}^{z}S_{2}^{y}=-S_{1}^{x}S_{2}^{x}$

第三项可以化简为

$\begin{aligned} -v_{\parallel}k_{x}\sigma_{y}\tau_{x}&=-v_{\parallel}(k_{1}\cos\theta-k_{3}\sin\theta)S_{2}^{y}(\beta S_{2}^{y}S_{1}^{y}-\alpha S_{1}^{x})\\&=-v_{\parallel}k_{1}\cos\theta(\beta S_{2}^{y}S_{2}^{y}S_{1}^{y}-\alpha S_{2}^{y}S_{1}^{x})+v_{\parallel}k_{3}\sin\theta(\beta S_{2}^{y}S_{2}^{y}S_{1}^{y}-\alpha S_{2}^{y}S_{1}^{x})\\&=-v_{\parallel}k_{1}\cos\theta(\beta S_{1}^{y}-\alpha S_{2}^{y}S_{1}^{x})+v_{\parallel}k_{3}\sin\theta(\beta S_{1}^{y}-\alpha S_{2}^{y}S_{1}^{x})\label{eq9} \end{aligned}$

整理(\ref{eq6})-(\ref{eq9})可以得到

$\begin{aligned} H&=-m_{0}S_{1}^{z}+(v_{z}\alpha\sin\theta-v_{\parallel}\beta\cos\theta)k_{1}S_{1}^{y}+(v_{\parallel}\beta\sin\theta+v_{z}\alpha\cos\theta)k_{3}S_{1}^{y}\\ &+(v_{\parallel}\alpha\cos\theta+v_{z}\beta\sin\theta)k_{1}S_{2}^{y}S_{1}^{x}+(v_{z}\beta\cos\theta-v_{\parallel}\alpha\sin\theta)k_{3}S_{2}^{y}S_{1}^{x}-v_{\parallel}k_{1}S_{2}^{x}S_1^x \label{eq10} \end{aligned}$

到这里之后，变量代换完成，在前面提到过，为了满足(\ref{eq2})的关系，需要令

$\alpha^{2}+\beta^{2}=1$

这是两个未知量，只有一个方程，为了确定这两个未知量，这里令

$(v_{z}\beta\cos\theta-v_{\parallel}\alpha\sin\theta)=0$

则可以得到

$\alpha=\frac{v_{z}\cos\theta}{v_{3}}\quad\beta=\frac{v_{\parallel}\sin\theta}{v_{3}}\quad v_{3}=\sqrt{(v_{z}\cos\theta)^{2}+(v_{\parallel}\sin\theta)^{2}}\label{eq11}$

将(\ref{eq11})代入(\ref{eq10})之后即可以将其化简为

$H=-m_{0}S_{1}^{z}+(v_{3}k_{3}+v_{0}k_{1})S_{1}^{y}+v_{1}k_{1}S_{2}^{y}S_{1}^{x}-v_{\parallel}k_{1}S_{2}^{x}S_1^x$

这里有

$v_{0}=\frac{(v_{z}^{2}-v_{\parallel}^{2})\cos\theta\sin\theta}{v_{3}}\quad v_{1}=\frac{v_{z}v_{\parallel}}{v_{3}}$