这里整理一下如何推导Graphene的紧束缚模型哈密顿量。
晶格结构
首先来分析石墨烯的晶体结构
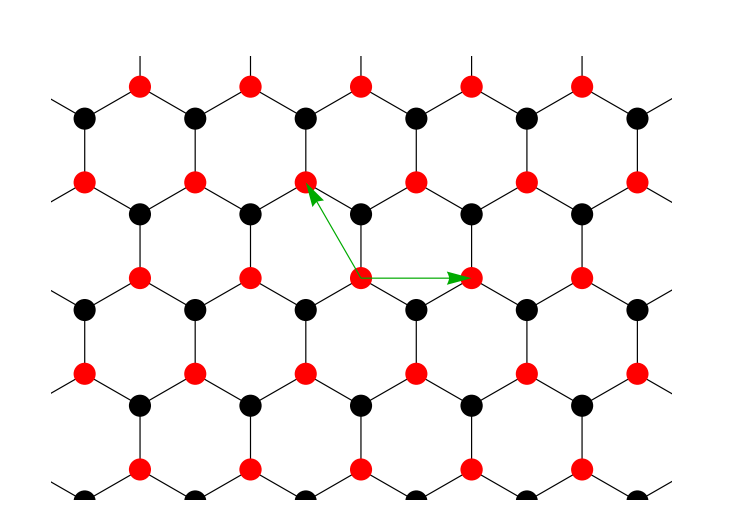
每个原胞中包含两个不等价的C原子,晶格基矢选择为
\[a_1=(\frac{3}{2},\frac{\sqrt{3}}{2})a\quad a_2=(\frac{3}{2},-\frac{\sqrt{3}}{2})a\]这里的$a$是晶格常数,对应的到空间基矢可以计算得到
\[b_1=(\frac{2\pi}{3},\frac{2\sqrt{3}}{3})/a\quad b_2=(\frac{2\pi}{3},-\frac{2\sqrt{3}}{3})/a\]每个原子到其最近邻原子之间(不等价原子)的距离为
\[r_1=(\frac{1}{2},\frac{\sqrt{3}}{2})a\quad r_2=(\frac{1}{2},-\frac{\sqrt{3}}{2})a\quad r_3=(0,-1)a\]通过固体物理的知识,Bloch态与Wannier态之间为Fourier变换关系
\[\psi_{nl}(r)=\frac{1}{\sqrt{N}}\sum_le^{ik\cdot l}W_n(r,l)\]这里的$W_n(r,l)$就是关于$(r-l)$的Wannier函数,在这里先不考虑多条能带的情况,所以将能带指标$n$先略去,此时因为每个原胞中包含两个C原子,而且它们对应的空间位置是不等价的,可以分别给每个不等价的C原子给定一个Bloch态
\[\varphi_1=\frac{1}{\sqrt{N}}\sum_le^{i\mathbf{k}\cdot \mathbf{R}^A_l}\phi(\mathbf{r}-\mathbf{R}_l^A)\quad \varphi_2=\frac{1}{\sqrt{N}}\sum_le^{i\mathbf{k}\cdot \mathbf{R}^B_l}\phi(\mathbf{r}-\mathbf{R}_l^B)\]这里的$N$就是体系中总的原胞的数目,$\mathbf{R}_l^{A/B}$则分别表示原胞中两个不等价的原子的位置。一般情况下都会使用原子的轨道波函数$\phi$来近似的代替局域的Wannier函数$W$,主要是因为两者都具有很好的局域性质,通常这都是一个比较好的近似。 接下来就可以将整个系统的波函数写成这些原子轨道波函数的线性组合
\[\psi(\mathbf{r})=c_1\varphi_1+c_2\varphi_2=\frac{1}{\sqrt{N}}\sum_{l,l^{'}}[e^{i\mathbf{k}\cdot \mathbf{R}^A_l}c_1\phi(\mathbf{r}-\mathbf{R}_l^A)+e^{i\mathbf{k}\cdot \mathbf{R}^B_{l^{'}}}c_1\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^B]\]下面的问题就是求解系统对应的本征方程
\[H\rvert\psi\rangle=E\rvert\psi\rangle\]这里就可以利用原子轨道波函数之间的正交关系
\[\lang\varphi_i\rvert\varphi_j\rangle=\delta_{ij}\]就可以将本征方程转化为一个救起方程
\[\[ \begin{array} H_{11}-E& H_{12}\\ H_{21}&H_{22}-E \end{array} \]=0\]这里使用了$H_{ij}=\langle\varphi_i\rvert H\rvert\psi_j\rangle\quad H_{12}=H_{21}^{*}$。通过求解这个方程就可以得到系统对应的本征能量
\[E=\frac{1}{2}[H_{11}+H_{22}\pm\sqrt{[(H_{11}-H_{22})^2+4\rvert H_{12}\rvert ^2]}]\]下面的问题就是计算这些具体的矩阵元到底是多少。
\[H_{11}=\langle\varphi_1\rvert H\rvert\varphi_1\rangle=\frac{1}{N}\sum_{ll^{'}}e^{-i\mathbf{k}\cdot(\mathbf{R}_l^A-\mathbf{R}_{l^{'}}^A)}\langle\phi(\mathbf{r}-\mathbf{R}_l^A)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle\]这里利用原子轨道波函数的正交性以及$\delta$函数的性质可以得到
\[\langle\phi(\mathbf{r}-\mathbf{R}_l^A)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\epsilon_{1}\langle\phi(\mathbf{r}-\mathbf{R}_l^A)\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\epsilon_1\] \[\delta(\mathbf{R}_l^A-\mathbf{R}_{l^{'}}^A)=\frac{1}{N}\sum_{ll^{'}}e^{-i\mathbf{k}\cdot(\mathbf{R}_l^A-\mathbf{R}_{l^{'}}^A)}\]就可以得到$H_{11}=\epsilon_1$。用力可以得到
\[H_{22}=\langle\varphi_2\rvert H\rvert\varphi_2\rangle=\frac{1}{N}\sum_{ll^{'}}e^{-i\mathbf{k}\cdot(\mathbf{R}_l^B-\mathbf{R}_{l^{'}}^B)}\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^B)\rangle=\epsilon_2\]而对于交叉项
\[H_{12}=\langle\varphi_1\rvert H\rvert \varphi_2\rangle=\frac{1}{N}\sum_{ll^{'}}e^{i\mathbf{k}\cdot(\mathbf{R}_l^B-\mathbf{R}_{l^{'}}^A)}\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\frac{1}{N}\sum_{ll^{'}}e^{i\mathbf{k}\cdot(\mathbf{R}_l^B-\mathbf{R}_{l^{'}}^A)}J\]这里简记
\[J=\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle\]被称为交叠积分,通常在计算中将它取定为一个常数,一般可以将其表示为
\[J=\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert H\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert (H_a+V-v_a)\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle\]这里是将这个系统的哈密顿量分解成了单粒子哈密顿量$H_a$与势能部分$V-v_a$,而对于单粒子部分有
\[\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert H_a\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\epsilon_1\times \langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle=\epsilon_1\delta_{AB}\delta_{ll^{'}}\]这里是利用了原子轨道波函数正交归一的性质,所以最终可以得到交叠积分为
\[J=\langle\phi(\mathbf{r}-\mathbf{R}_l^B)\rvert (V-v_a)\rvert\phi(\mathbf{r}-\mathbf{R}_{l^{'}}^A)\rangle\]这里来看在$H_{12}$中其实包含了$\frac{1}{N}\sum_{ll^{‘}}$,也就是说它是包含了所有的格点上的hopping,而实际上在考虑的时候可以仅关注最近邻之间的hopping(但是并不意味着所有的系统都可以只关注最近邻,有时候其它近邻会产生较大的影响,需要具体问题具体对待)
\[\rvert \mathbf{R}_l^A-\mathbf{R}_{l^{'}}^B\rvert=\rvert r_i\rvert\]所以此时遍历三个最近邻hopping方向
\[r_1=(\frac{1}{2},\frac{\sqrt{3}}{2})a\quad r_2=(\frac{1}{2},-\frac{\sqrt{3}}{2})a\quad r_3=(0,-1)a\]就可以得到
\[H_{12}=\frac{1}{N}\sum_{ll^{'}}e^{i\mathbf{k}\cdot(\mathbf{R}_l^A-\mathbf{R}_{l^{'}}^B)}J=\frac{1}{N}(e^{i\mathbf{k}\cdot\mathbf{r}_1}+e^{i\mathbf{k}\cdot\mathbf{r}_2}+e^{i\mathbf{k}\cdot\mathbf{r}_3})NJ=J[e^{ik_x\cdot a}+2\cos k_y(\frac{\sqrt{3}a}{2}\cdot e^{ik_x\cdot\frac{a}{2}})]\]最后就可以得到石墨烯紧束缚模型对应的能带本征值
\[E(\mathbf{k})=\epsilon_1\pm J\sqrt{3+2\cos(\sqrt{3}k_ya)+4\cos(\frac{3}{2}k_xa)\cos(\frac{\sqrt{3}}{2}k_ya)}\]到此就推导完了石墨烯的紧束缚哈密顿量模型以及求解其对应的能量本征值。
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |