这里整理一下ARPES的理论原理，搞清楚一下到底它测量的是什么物理量。

基本原理

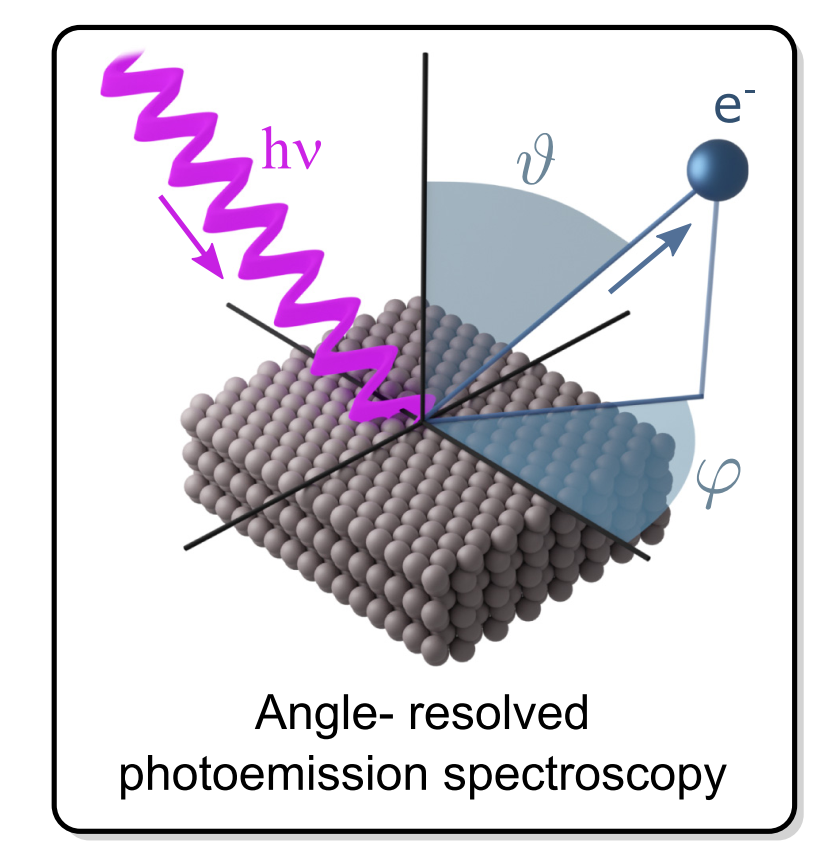
Angle-resolved photoemission spectroscopy (ARPES)的基本原理是基于光电效应，利用一束光对材料进行照射，将材料中的电子进行激发，可以探测逃逸电子的动能和动量分布，实验示意图如图1所示

一般情况下固体系统都可以通过一个哈密顿量$H$的本征值和本征态来描述，最简单的情况就是系统的行为主要由电子的动能和晶体的周期势场来决定的时候，此时可以通过能带理论来很好的描述体系，其电子波函数$\psi(\mathbf{r})$是Bloch态，而本征值$\epsilon(\mathbf{k})$那表示着能量为$\mathbf{k}$的时候电子能带的色散关系，但是对于很多系统，其中的电子关联效应不可忽略，那么能带理论就不再能描述这类系统。但是即使是多体系统中，电子仍然是参与其中的，那么仍然是可以通过研究电子的的能量-动量谱来研究这类系统的性质，如图2所示

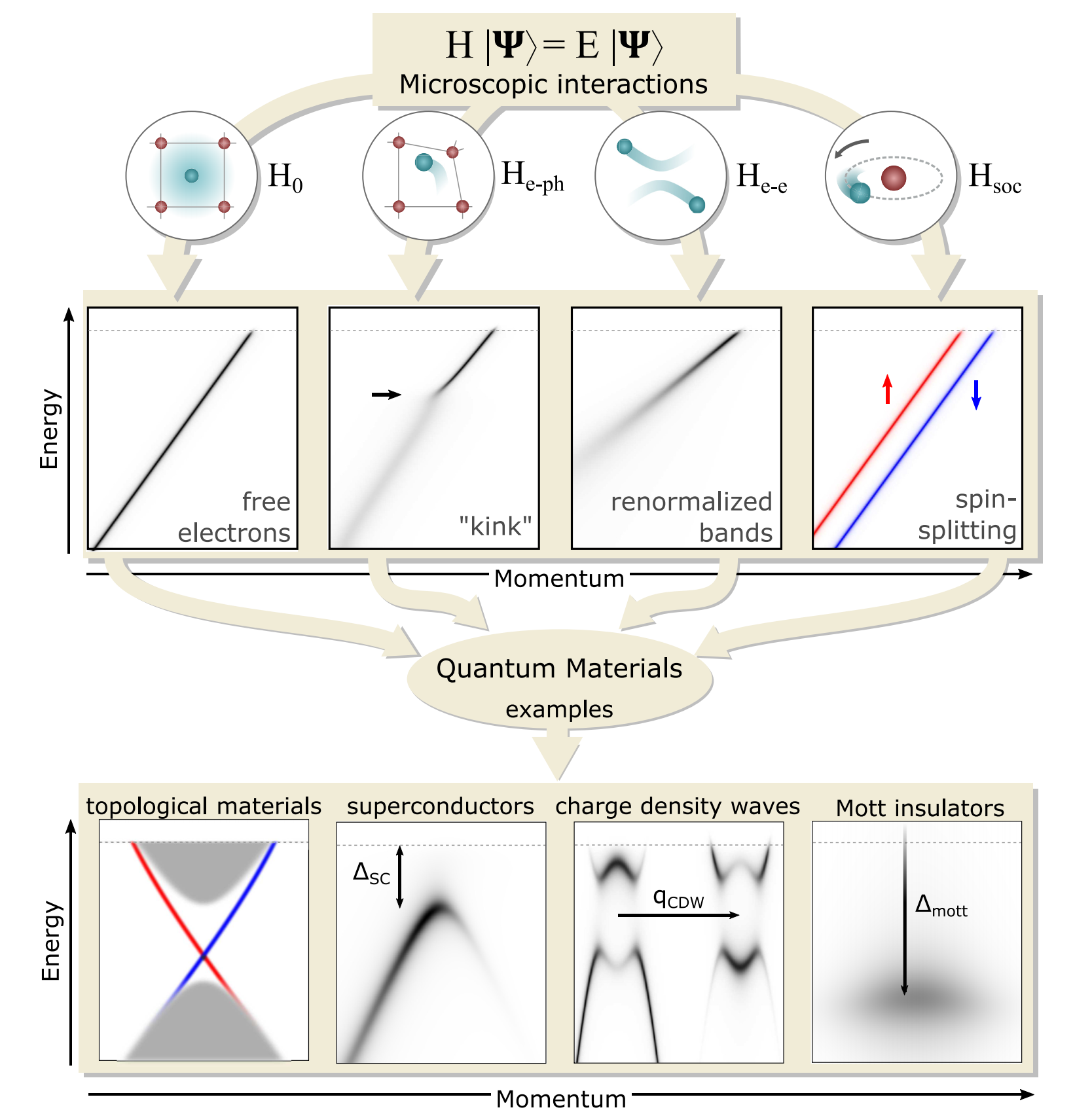
在相互作用比较弱的时候。ARPES能谱的强度可以反映电子的能带结构$\epsilon(\mathbf{k})$，从能带结构同样可以得到体系的费米速度以及费米面的结构信息。

由光电效应可以知道，当光子照射到材料上被电子吸收之后，电子可以从材料中逃逸，可以利用这个过程中的运动学方程反推出电子在材料中的束缚能$E_B$以及晶体动量$\hbar\mathbf{k}$。一般情况下在ARPES的实验中都是利用一束单色光能量为$h\nu$照射单晶材料，在所有的方向上探测辐射电子，其中的一部分电子会被光子探测仪收集并记录其这些电子的动能$E_\text{kin}$和发射角度$(\theta,\varphi)$，从图\ref{f1}中可以看到，这里的$\theta$角是相对于单晶表面的法向分量而言的，$\varphi$则是通常所说的方位角，它是以实验仪器的结构或者晶轴的方向为基准确定的。实验中探测到的动能是以样品的真空能级为为零点来定义的，利用动量和能量守恒定律可以得到发射前后电子态的能量动量关系

\[\begin{equation} \begin{aligned} E_\text{kin}&=h\nu-\phi-E_B\\ \hbar\mathbf{k}_\parallel&=\sqrt{2mE_\text{kin}}\sin(\theta)\label{q3} \end{aligned} \end{equation}\]

这里其实是忽略了光子的动量，因为在紫外区间内，它的动量是可以忽略的。$\phi$是样品表面的功函数$\hbar\mathbf{k}$是平行于晶体表面方向电子的动量，$E_\text{kin}$是光电动能，$E_B$是电子在被激发之前的束缚能。晶体在面内的具有离散周期性结构，因此动量$\mathbf{k}\parallel$在整个过程中是守恒的，而垂直表面方向的动量$\mathbf{k}\perp$在电子的激发过程中是不守恒的。

光电发射过程如图3所示

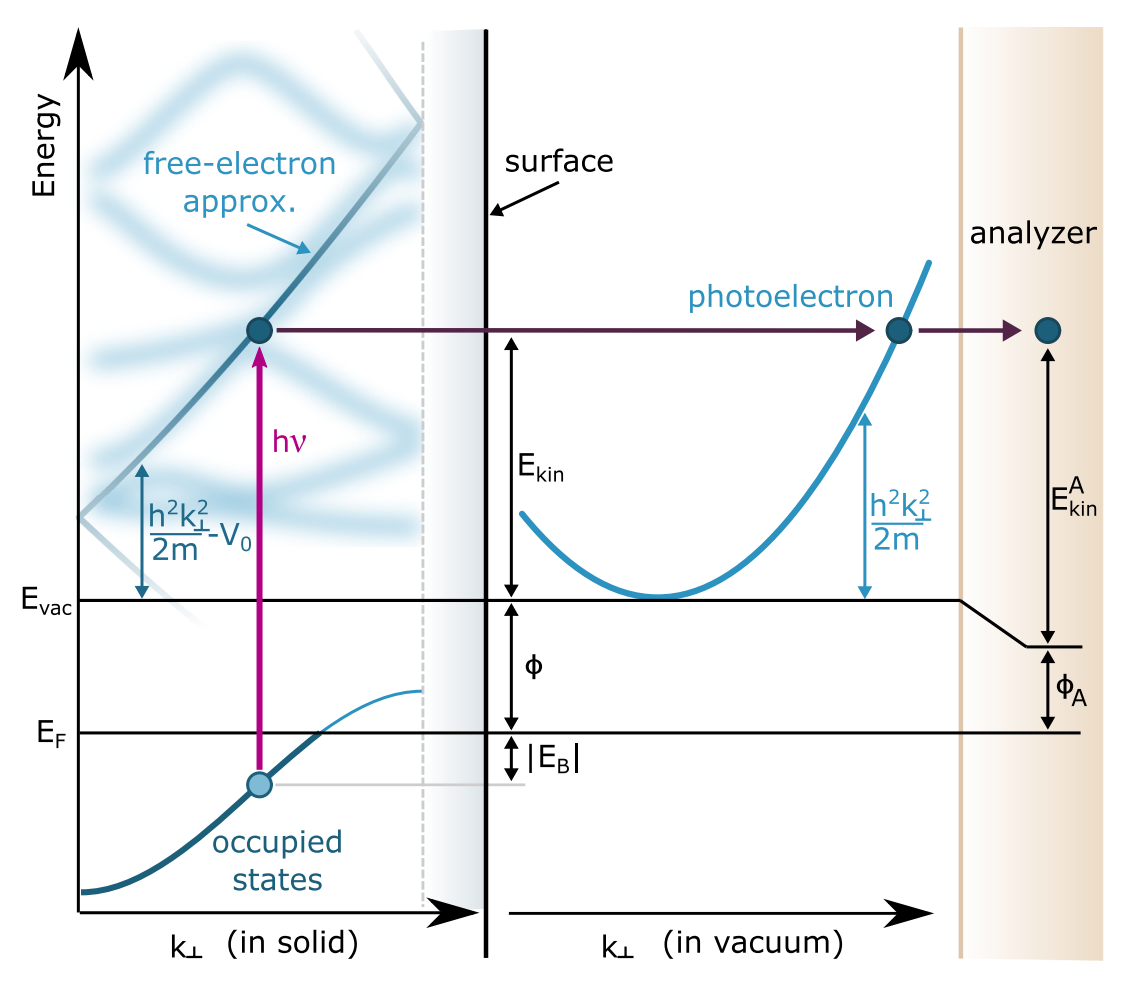
相比较于直接给出$E_\text{kin}$与入射光照能量$h\nu$之间的关系，ARPES的数据给出的是$E-E_f=-E_B$这个能量信息，直接反映初始状态下电子的能量信息，这里的$E_F$则是样品的费米能级。利用费米黄金规则可以直接给出在光电发射过程中系统从初始状态$\rvert\Psi_i^N\rangle$到被激发末态$\rvert\Psi_f^N$的几率

\[\begin{equation} w_{fi}=\frac{2\pi}{\hbar}\rvert \langle\Psi_f^N\rvert H_{int}\rvert \Psi_i^N\rangle\rvert^2\delta(E_f^N-E_i^N-h\nu)\label{q1} \end{equation}\]

这里的能量$E_i^N,E_f^N$分别是$N$电子体系初态和终态的能量，而$H_\text{int}$描述的是电子-光子相互作用的微扰哈密顿量

\[\begin{equation} \begin{aligned} H_\text{int}&=\frac{1}{2m}(\mathbf{p}+\frac{e}{c}\mathbf{A})^2-e\Phi-\frac{\mathbf{p}^2}{2m}\\ &\simeq\frac{e}{2mc}(\mathbf{A}\cdot\mathbf{p}+\mathbf{p}\cdot\mathbf{A})\\ &\simeq\frac{e}{2mc}\mathbf{A}\cdot\mathbf{p} \end{aligned} \end{equation}\]

这里$\mathbf{p}$是电子的动量算符，$\mathbf{A},\Phi$分别是电磁场的矢势和标势，而在上面的过程中选择了Weyl规范，将标势$\Phi=0$，这里使用了两个近似步骤，第一步是忽略了两光子过程$\mathbf{A}^2$，第二个近似则是认为光场$\mathbf{A}$在原子范围内是常数

\[\begin{equation} [\mathbf{A},\mathbf{p}]\sim\nabla\cdot\mathbf{A}=0. \end{equation}\]

这里还有一点需要强调，费米黄金规则是有在弱微扰下才是有效的，如果是一束强度较大的超快激光脉冲，那么上面的微扰过程就需要进行修正，必须包含多光子过程才可以。

方程(\ref{q1})描述的其实是个一步模型，光子吸收，电子激发，电子探测被当作一个相关联的过程。但是从实用主义的角度来讲，为了方便通常是将光电激发这个过程唯象的分为三步

• 光子驱动材料中的电子直接发生光学跃迁(这个步骤中会包含材料本征的电子结构信息)。

• 电子传播到材料表面(这个过程是根据弹性和非弹性散射过程中的平均自由程$\lambda_\text{MFP}$来描述的)。

• 电子穿过表面势垒，电子最终在真空中占据自由电子平面波状态，并延伸至检测器。

这个三步模型的优势在于每一步其实都是解耦的。

为了得到一个更加直观的图像来理解光电发射过程，这里从无相互作用的电子系统出发来理解，首先考虑一个N电子体系的初态和终态

\[\begin{equation} \begin{aligned} \rvert\Psi_f^N\rangle&=A\rvert\phi_f^\mathbf{k}\rangle\otimes\rvert\Psi_f^{N-1}\rangle\\ \rvert\Psi_i^N\rangle&=A\rvert\phi_i^\mathbf{k}\rangle\otimes\rvert\Psi_i^{N-1}\rangle\\ \end{aligned}\label{q6} \end{equation}\]

这里的$A$是反对称算符，系统需要满足Pauli不相容原理，$\rvert\phi_i^\mathbf{k}\rangle,\rvert\phi_f^\mathbf{k}\rangle$是吸收光子之前和之后电子的波函数，因为动量守恒的缘故，这两个态对应的动量都是$\mathbf{k}$，初态和终态的能量分别是$\epsilon_i,\epsilon_f$，$\rvert\Psi_i^{N-1}\rangle,\rvert \Psi_f^{N-1}\rangle$是剩下的$(N-1)$个电子系统对应的初态和终态。因为这里考虑的是无相互作用系统，所以从$N$电子系统中移走一个电子，并不会对$(N-1)$个电子的系统有影响，因此

\[\begin{equation} \rvert \Psi_i^{N-1}\rangle=\rvert \Psi_f^{N-1}\rangle \end{equation}\]

下面就来利用费米黄金规则计算整个过程中的光电流$I=\sum_{if}w_{fi}$，这里继续做一个假设，在每个动量$\mathbf{k}$上至少有一个$(i\rightarrow f)$的跃迁发生，那么就可以得到

\[\begin{equation} \begin{aligned} &I_{i\rightarrow f}\sim\rvert M_{f,i}^\mathbf{k}\rvert^2\delta(\epsilon_f-\epsilon_\mathbf{k}-h\nu)\\ &M_{f,i}^\mathbf{k}\equiv\langle\phi_f^\mathbf{k}\rvert H_{int}\rvert \phi_i^\mathbf{k}\rangle\label{q2} \end{aligned} \end{equation}\]

这里的$M_{f,i}^\mathbf{k}$是单电子的偶极矩阵元，其实也就是跃迁选择定则。从方程(\ref{q2})就可以从一个即理论又实验的角度来理解到底ARPES是如何反映材料的能带信息的。首先可以看到这里有一个$\delta$函数，所以当

\[\begin{equation} \epsilon_f-\epsilon_\mathbf{k}-h\nu=0 \end{equation}\]

的时候，就可以在ARPES的能谱上看到一个非常尖锐的峰，这也就是相当于探测到了材料的能带$\epsilon(\mathbf{k})$，而这个峰的强度则是由偶极矩阵元$M_{f,i}^\mathbf{k}$所决定的。所以这里也就可以看到为什么ARPES可以探测材料的能带结构。{\color{red}这里的讨论都是基于无相互作用的情形，如果存在电子相互作用，那么这个图像是要被修改的。}

这里继续来回顾一下前面提到的三步模型，在第一步电子吸收光子的过程中，动量$\mathbf{k}$的所有分量都是守恒的，但是在第三步中电子电子穿过表面势垒激发之后平行于表面的动量$\mathbf{k}\parallel$是守恒的。这里如果做一些假设同样是可以得到垂直方向的动量$\mathbf{k}{\perp\text{solid}}$，假设在晶体中末态光电子的色散关系可以用自由电子色散关系和一个能量偏移来描述

\[\begin{equation} \epsilon_f=\frac{\hbar^2\mathbf{k}^2_{\perp\text{solid}}}{2m}-V_0 \end{equation}\]

这个$V_0$被称为内势，就先简单的把它当作一个参数来理解就可以。假设光电子在表面没有受到非弹性碰撞，它在固体中的终态能量可以等同于真空中的动能

\[\begin{equation} E_\text{kin}=\frac{\hbar^2\mathbf{k}_\text{vac}^2}{2m} \end{equation}\]

这里就可以看到前面提到的内势$V_0$就反映出了动量$\mathbf{k}_\perp$在表面上的不连续性

\[\begin{equation} \frac{\hbar^2\mathbf{k}^2_\text{vac}}{2m}=\frac{\hbar^2\mathbf{k}^2_{\perp\text{solid}}}{2m}-V_0 \end{equation}\]

从而就可以得到

\[\begin{equation} \hbar\mathbf{k}_{\perp\text{solid}}=\sqrt{2m[E_\text{kin}\cos^2(\theta)+V_0]}\label{q4} \end{equation}\]

从光电效应的方程(\ref{q3})看到，动能$E_\text{kin}$是依赖于入射光子能量$h\nu$的，因此利用方程(\ref{q4})之后，通过调节入射光的频率就可以得到$\hbar\mathbf{k}_{\perp\text{solid}}$的色散关系，而这里的$V_0$是一个可以通过实验和方程(\ref{q3})决定的量，并利用下面的关系

\[\begin{equation} E_B(\mathbf{k}_\parallel,\mathbf{k}_{\perp\text{solid}})=E_B(\mathbf{k}_\parallel,\mathbf{k}_{\perp\text{solid}}+n\mathbf{G}_\perp) \end{equation}\]

这里$\mathbf{G}\perp$是平面外的倒空间晶格矢量，可以看到两位电子态并不会随着 $\mathbf{k}{\perp\text{solid}}$存在色散，从而可以通过$h\nu$以来的测量来区分表面和体态的能带。

这里表面的色散关系只是依赖于平面内的动量$\mathbf{k}\parallel$， 但是体态的能带色散关系同时依赖于$(\mathbf{k}\parallel,\mathbf{k}_{\perp\text{solid}})$， 因此通过改变入射光子的能量$h\nu$就可以区分到底哪些是体态的能带mapping，哪些是表面的能带mapping。

固体材料中电子的非弹性碰撞平均自由程$\lambda_\text{MFP}$会使得光电子在材料表面上开始衰减 ，这个效应比较依赖于电子的功能，而于材料本身没有太大的关系，当能量在20-100eV的时候平均自由程的最小值小于1nm， 这意味着使用紫外光源执行的 ARPES 对表面高度敏感，大部分信号来自顶部的几个原子层。所以这就要求材料的表面需要非常的平整， 这样才可能通过ARPES来获得材料体态的信息。

影响ARPES分辨率的因素有很多，可以分为内在影响和外部影响。

• 内在因素1

其中重要的一个内在影响就是终态的寿命，电子处在某个态的寿命因为散射存在缘故总是有效的，而这个散射通常又是和平均自由程相关$\lambda_\text{MPF}$的，因此利用不确定原理可以估算位置-动量不确定关系

\[\begin{equation} \Delta\mathbf{k}_\perp\simeq\frac{\hbar}{\lambda_\text{MPF}} \end{equation}\]

对于一些典型能量$h\nu$下的分辨率展宽为

\[\begin{equation} \Delta\mathbf{k}_\perp\sim 0.1 A^{-1} \end{equation}\]

• 内在因素2

另外一个影响分辨率的内在因素就是在前面提到的偶极近似不适用

\[\begin{equation} \nabla\cdot\mathbf{A}=0 \end{equation}\]

实际上如果在表面附近介电函数发生突然的变化，将会使得$\mathbf{A}$在表面附近的原子尺度范围内发生很大的变化，这个时候偶极近似也就不再适用了，突然变化的$\mathbf{A}$同样会影响光电子的动量并且对$\mathbf{k}_\parallel$产生一个不确定的展宽。

• 外在因素1

在实验过程中样品的质量和样品表面的质量不好，会产生杂质散射，从而会使得能量分辨率变低从而产生展宽。

• 内在因素2

另外一个影响观测的因素就是实验上的能量分辨率，通常情况下入射的光束也是存在一定的能量展宽的，对应的能量分辨率为

\[\begin{equation} (\Delta E_\text{tot})^2=(h\Delta\nu)^2+(\Delta E_\text{spec})^2 \end{equation}\]

这里$h\Delta\nu$所带来的动量展宽是可以忽略的，能对动量展宽带来比较大的影响的则是光谱仪的角度分辨率$\Delta\theta$

\[\begin{equation} \hbar\Delta\mathbf{k}_\parallel=\sqrt{2mE_\text{kin}}\cos(\theta)\Delta\theta \end{equation}\]

从上面的分析中其实可以看到，ARPES所能看到的最深的能级$E_B$完全是有入射光的能量$h\nu$所决定的

\[\begin{equation} E_B^\text{max}=h\nu-\phi \end{equation}\]

最大的$\mathbf{k}_\parallel$为

\[\begin{equation} \hbar\mathbf{k}_\parallel^\text{max}=\sqrt{2m(h\nu-\phi)} \end{equation}\]

矩阵元效应

前面在通过三步模型介绍ARPES的基本原理的时候已经介绍过偶极矩阵元$M_{f,i}^\mathbf{k}$，

\[\begin{equation*} \begin{aligned} &I_{i\rightarrow f}\sim\rvert M_{f,i}^\mathbf{k}\rvert^2\delta(\epsilon_f-\epsilon_\mathbf{k}-h\nu)\\ &M_{f,i}^\mathbf{k}\equiv\langle\phi_f^\mathbf{k}\rvert H_{int}\rvert\phi_i^\mathbf{k}\rangle \end{aligned} \end{equation*}\]

通过对偶极矩阵中的元素进行分析，在实验上可以通过ARPES探测出关于初态$\rvert\phi_i^\mathbf{k}\rangle$的波函数的微观信息。例如，当电子在样品的镜面对称平面上光发射时，$\rvert\phi_i^\mathbf{k}\rangle$ 的奇偶性可以通过测量各种线偏光的发射强度推导出来。利用这个手段可以探测能带所对应的轨道信息。利用左旋或者右旋的光泽可以用来探测时间反演对称的电子态，还可以用来探测拓扑绝缘体中的自旋动量锁定态，以及手性、Berry位相还有Dirac电子。

利用极化的光在有自旋轨道耦合的系统中探测光电子的自旋也是ARPES的一个重要表征手段，初始态可以看作是不同自旋态的线性叠加

\[\begin{equation} \rvert\phi\rangle=\sum_\alpha c_{\alpha,\uparrow}\rvert\alpha,\uparrow\rangle+c_{\alpha,\downarrow}\rvert\alpha,\downarrow\rangle \end{equation}\]

这里的$\alpha$表示的是不同的轨道索引，光偏振以及轨道的空间对称性决定了波函数的哪些分量是光发射的，从而就可以通过改变光的极化来探测不同自旋取向的态，也就是自旋分别的ARPES。

多体系统

对于存在相互作用的体系，它与无相互作用时候最大的不同就是多体的初态和末态不能直接分解为方程(\ref{q6})的形式，但是如果在某些近似的条件下，这个形式仍然是可以适用的。这里先做一个假设，{\color{blue}认为在系统中拿走一个电子是一个瞬时过程，称为瞬时近似}，在这个近似下光电子会具有很高的终态，因此不会有时间与剩余的$(N-1)$个电子发生相互作用，所以此时就可以使用

\[\begin{equation} \rvert\Psi_f^N\rangle=A\rvert\phi_f^\mathbf{k}\rangle\otimes\rvert\Psi_f^{N-1}\rangle \end{equation}\]

来描述末态，而初态则是利用平均场的方法来描述，所以此时的初态与无相互作用的初态是完全不同的，{\color{blue}$(N-1)$个电子的系统不再可以看作是从$N$电子系统中移走一个电子的态}

\[\begin{equation} \rvert\Psi_i^{N-1}\rangle\neq\rvert\Psi_f^{N-1}\rangle \end{equation}\]

在瞬时近似假设下，$(N-1)$个电子的终态可以处在任意数量的激发态，其本征波函数为$\rvert\Psi_m^{N-1}\rangle$对应的本征能量为$E_m^{N-1}$，那么总的转移几率就是所有的激发态求和

\[\begin{equation} \sum_{f,i}\rvert M^\mathbf{k}_{f,i}\rvert^2\sum_m\rvert\langle \Psi_m^{N-1}\rvert\Psi_i^{N-1}\rvert^2\delta(\epsilon_f+E_m^{N-1}-E_i^{N}-h\nu) \end{equation}\]

这里$\rvert M^\mathbf{k}_{f,i}\rvert^2$就是从初态$i$中拿走一个电子剩下$(N-1)$个电子处在激发本征态$m$上的几率。而对于强关联材料，这会在能谱上反映出丰富的信息，包括能带展宽等。利用格林函数可以写出从系统中移走一个单电子的谱函数$A^{-}(\mathbf{k},\omega)$

\[\begin{equation} A^{-}(\mathbf{k},\omega)=\sum_m\rvert\langle\Psi_m^{N-1}\rvertc_\mathbf{k}\rvert\Psi^N_i\rvert^2\delta(\omega-E_m^{N-1}+E_i^N) \end{equation}\]

物理上$A^{-}(\mathbf{k},\omega)$表示剩余的$(N-1)$个电子系统移走一个波矢$\mathbf{k}$的电子之后能量变化为$\omega$的概率，$A^{-}(\mathbf{k},\omega)$与完全谱函数$A(\mathbf{k},\omega)$之间的关系是

\[\begin{equation} A^{-}(\mathbf{k},\omega)=A(\mathbf{k},\omega)f(\omega) \end{equation}\]

这里的$f(\omega)$是费米分布函数，最终就可以得到光发射强度为

\[\begin{equation} I(\mathbf{k},\omega)=I_0(\mathbf{k},h\nu,\mathbf{A})f(\omega)A(\mathbf{k},\omega) \end{equation}\]

在瞬时近似假设下，光发射强度的信号正比于单粒子的谱函数。

这里的$f(\omega)$是因为光电子发射只能从占据态的电子中激发，这也就说明ARPES只能探测费米面一下的能带，而$I_0(\mathbf{k},h\nu,\mathbf{A})$则代表着由于矩阵元效应带来的光强调制。

谱函数是与推迟格林函数相联系

\[\begin{equation} G(\mathbf{k},\omega)=\frac{1}{\omega-\epsilon(\mathbf{k})-\Sigma(\mathbf{k},\omega)}\quad A(\mathbf{k},\omega)=-\frac{1}{\pi}\text{Im}G(\mathbf{k},\omega) \end{equation}\]

这里相互作用可以通过自能来描述

\[\begin{equation} \Sigma(\mathbf{k},\omega)=\Sigma^{'}(\mathbf{k},\omega)+i\Sigma^{'}(\mathbf{k},\omega) \end{equation}\]

从而可以得到谱函数为

\[\begin{equation} A(\mathbf{k},\omega)=-\frac{1}{\pi}\frac{\Sigma^{''}(\mathbf{k},\omega)}{[\omega-\epsilon(\mathbf{k})-\Sigma^{'}(\mathbf{k},\omega)]^2+[\Sigma^{''}(\mathbf{k},\omega)]^2} \end{equation}\]

从这里就可以看到，自能中的$\Sigma^{‘}(\mathbf{k},\omega)$将会对电子能带$\epsilon(\mathbf{k})$进行平移修正，而$\Sigma^{‘’}$则会使得能谱进行展宽，物理上自能的虚部代表着单粒子的散射率，代表着准粒子的寿命。上面的这些分析是可以退化到无相互作用情况

\[\begin{equation} \Sigma(\mathbf{k},\omega)=0\quad A(\mathbf{k},\omega)=\delta(\omega-\epsilon(\mathbf{k})) \end{equation}\]

在弱相互作用下电子的自能$\Sigma(\mathbf{k},\omega)$可以展开到关于能量$\epsilon(\mathbf{k})$的一阶近似，此时谱函数为

\[\begin{equation} A(\mathbf{k},\omega)=Z(\mathbf{k})\frac{\Gamma(\mathbf{k})/\pi}{(\omega-\epsilon(\mathbf{k}))^2+\Gamma(\mathbf{k})^2}+A_\text{inc}(\mathbf{k},\omega) \end{equation}\]

这里的一些符号为

\[\begin{equation*} Z(\mathbf{k})=(1-\partial\Sigma^{'})^{-1}\quad\epsilon(\mathbf{k})=Z(\mathbf{k})(\epsilon(\mathbf{k})+\Sigma^{'})\quad\Gamma(\mathbf{k})=Z(\mathbf{k})\rvert\Sigma^{''}\rvert \end{equation*}\]

这里自能和求导都是在$\omega=\epsilon(\mathbf{k})$的位置进行的，而且这个描述在费米面附近当满足条件

\[\begin{equation} \rvert\Sigma^{''}\rvert<<\epsilon(\mathbf{k}) \end{equation}\]

在$\omega,\rvert\mathbf{k}-\mathbf{k}F\rvert$比较小的情况下仍然是有效的。$A\text{inc}$是谱函数的非相干部分，表示着由于自能$\Sigma(\mathbf{k},\omega)$在一阶近似带来的误差，而且$A_\text{inc}$需满足求和规则。

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。