BBH Nested Wilson loop计算(Julia 并行)
这里就使用Julia写了一下Nested Wilson loop的并行程序,因为前面考虑的体系其实就是一个$4\times 4$的哈密顿量,如果体系变大以及计算撒点数量变大的时候,julia还是会有点慢,这里就给一个并行的版本,并顺便看一下julia是怎么并行的。
{:.info}
Nested Wilson Loop
关于Nested Wilson loop的计算可以参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators 这篇文章,这里主要说一下自己在学习计算的时候踩过的坑。
与计算Wilson loop相同,这里最主要的仍然是找到一个Wannier band basis,也就是文章的中的公式
其实在做计算的时候,最让人困扰的不过是公式中的一大堆符号对应的到底是什么,这里就来讲这个公式拆解开,一步一步的讲清楚里面的含义。这里假设你已经知道为什么要计算Nested Wilson loop,
我在这里就简单的阐述一下。首先要是体系的Wilson loop计算对应的Wannier哈密顿量的能带是有能隙的,也就是说你的体系是4带模型,那么当占据态是2条能带的时候,每个占据态能带会对应着一个Wannier center,
比如BHZ模型的两条占据态能带对应的Wannier band就是相互交叉的,而且因为Wilson loop与边界态之间的拓扑等价性,TI是有边界态的,所以其对应的Wilson loop在形状上就与边界态类似。而对于高阶拓扑相,
首先就是要使得边界态打开能隙,那么相对应的就是其Wilson loop计算得到的Wannier center随着某个动量参数的演化是不会相互交叉的,这一点在上面BBH模型中已经计算过了,所以此时就可以对某一个单独的Wannier band
计算它的Nested Wilson loop,所以首先第一步就是必须要明白什么样的情况下,是需要计算体系的Nested Wilson loop。
这里的$\sum_{n=1}^\text{Nocc}$不用讲太多,是需要对占据态进行求和,但是这个$n$其实表示的只是说哈密顿量的占据态,也就是说对于$\rvert u^n_\mathbf{k}\rangle$而言,这是哈密顿量的占据态波函数,$n$表示占据态其实是对$\rvert u^n_\mathbf{k}\rangle$
而言的,虽然$[v_{x,\mathbf{k}}^j]^n$中同样存在这个$n$,但是在这个地方$n$代表的不是占据态,在这里$j$代表的才是你选择的是哪一个Wannier band来计算其对应的Nested Wilson loop,也就是这里$j$代表的是你选择的是那个占据的Wannier band,而$n$在这里
表示的是一个Wannier哈密顿量本征矢量的第$n$个分量。假如$H_\text{Wann}$是Wannier哈密顿量,其满足
那么这里的$[v_{x,\mathbf{k}}^j]^n$表示的就是这个本征矢量的第$n$个分量,$j$则表示你选择是哪个本征值对应的本征矢量,也就是选择了哪一个Wannier band。这里的$x$则表示你在做Wilson loop的时候,是沿着哪个方向进行的,即就是讲上面公式中的$H_\text{Wann}$替换成你
构建的那个Wilson loop的哈密顿量就可以。
至于$\rvert u^n_\mathbf{k}\rangle$就很简单了,它表示的就是你的哈密顿量的本征态,当然了在计算的时候,还是要选择正确的占据态才可以。下面直接上代码,在其中同样做了注释1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193using DelimitedFiles
using ProgressMeter
using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
#--------------------------------------------------------------
function hamset(kx::Float64,ky::Float64)
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.000000000000
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
#--------------------------------------------------------------------------------------
function Wilson_kx(kx::Float64,nky::Int64)
# nky::Int64 = 100
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nky) # 存储哈密顿量对应的波函数
wan = zeros(ComplexF64,Nocc,Nocc) # 存储Wannier哈密顿量对应的波函数
F = zeros(ComplexF64,Nocc,Nocc)
kylist = range(0, 2*pi, length = nky)
for iy in 1:nky # 固定kx,沿着ky方向计算Wilson loop
ky = kylist[iy]
val,vec = eigen(hamset(kx,ky))
wave[:,:,iy] = vec[:,:] # 存储波函数
end
wave[:,:,nky] = wave[:,:,1] # 在边界上波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1 # 构建单位矩阵
end
for i1 in 1:nky - 1 # index ki lattice
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
F = wan * F # 沿着ky方向构造Wannier哈密顿量
end
val,vec = eigen(F) # 这里求解得到的本征态是按照本征值的大小进行排列的,和python有一点不同
vec1 = vec[:,sortperm(map(angle,val))[1]]
vec2 = vec[:,sortperm(map(angle,val))[2]]
return vec1,vec2# 给出两个占据态能带对应的Wannier哈密顿量的本征矢量
end
#-------------------------------------------------------------------------------------
function Wilson_ky(ky::Float64,nkx::Int64)
# nkx::Int64 = 100
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nkx)
wan = zeros(ComplexF64,Nocc,Nocc)
F = zeros(ComplexF64,Nocc,Nocc)
kxlist = range(0, 2*pi, length = nkx)
for ix in 1:nkx # 固定ky,沿着kx方向计算Wilson loop
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1
end
for i1 in 1:nkx - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
F = wan * F # 构造Wannier 哈密顿量
end
val,vec = eigen(F)
vec1 = vec[:,sortperm(map(angle,val))[1]]
vec2 = vec[:,sortperm(map(angle,val))[2]]
return vec1,vec2# 给出两个占据态能带对应的Wannier哈密顿量的本征矢量
# return sort(map(angle,val)/(2*pi))
end
#------------------------------------------------------------------------------------
function Nseted_Wilson_loop_kx(nkx::Int64)
# nkx::Int64 = 100
nky::Int64 = nkx
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
kxlist = range(-pi, pi, length = nkx)
kylist = range(-pi, pi, length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
for ix in 1:nkx
kx = kxlist[ix]
for iy in 1:nky
ky = kylist[iy]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,iy] = vec[:,:]
end
wave[:,:,nky] = wave[:,:,1] # 波函数首尾相接
wmu = zeros(ComplexF64,hn,nky) # 用来构建新的Wannier basis
for iy in 1:nky
ky = kylist[iy]
wann_v1, wann_v2 = Wilson_ky(ky,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,iy] = wave[:,1,iy] * wann_v1[1] + wave[:,2,iy] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nky] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for iy in 1:nky - 1
F0 = wmu[:, iy]' * wmu[:, iy + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
#pmu = log(wan)/(2 * im * pi)
pmu = map(angle,wan)/(2*pi)
if pmu < 0
pmu += 1
end
pmulist[ix] = pmu
end
return kylist,pmulist
end
#-----------------------------------------------------------------------
function Nseted_Wilson_loop_ky(nkx::Int64)
# nkx = 100
nky = nkx
hn = 4
Nocc = Int(hn/2)
kxlist = range(-pi,pi,length = nkx)
kylist = range(-pi,pi,length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
for iy in 1:nky
ky = kylist[iy]
for ix in 1:nkx
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1]
wmu = zeros(ComplexF64,hn,nkx)
for ix in 1:nkx
kx = kxlist[ix]
wann_v1, wann_v2 = Wilson_kx(kx,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,ix] = wave[:,1,ix] * wann_v1[1] + wave[:,2,ix] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nkx] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for ix in 1:nkx - 1
F0 = wmu[:,ix]' * wmu[:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
#pmu = log(wan)/(2*im*pi)
pmu = map(angle,wan)/(2*pi)
if pmu < 0
pmu += 1
end
pmulist[iy] = pmu
end
return kylist,pmulist
end
#----------------------------------------------------------------------------------------------
function Nested(num)
nkx = 100
x1,x2 = Nseted_Wilson_loop_ky(nkx)
fx1 = "Nested-ky-" * string(num) * ".dat"
f1 = open(fx1,"w")
writedlm(f1,[x1 x2],"\t")
close(f1)
x1,x2 = Nseted_Wilson_loop_kx(nkx)
fx1 = "Nested-kx-" * string(num) * ".dat"
f1 = open(fx1,"w")
writedlm(f1,[x1 x2],"\t")
close(f1)
end
#-----------------------------------------------------------------
# @time test()
Nested(1)
Julia并行
其实对于julia来说,并行还是还是非常方便的,首先加入几个函数库1
2
3using DelimitedFiles
using ProgressMeter
using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
这里使用@everywhere是为了让每个线程都可以看到这些库函数,接下来就是要对需要并行的函数,每个函数前面也都加入@everywhere。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 function hamset(kx::Float64,ky::Float64)
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.000000000000
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
最后一步就是需要对需要并行计算的循环进行修改1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 function Nseted_Wilson_loop_ky(nkx::Int64)
# nkx = 100
nky = nkx
hn = 4
Nocc = Int(hn/2)
kxlist = range(-pi,pi,length = nkx)
kylist = range(-pi,pi,length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
for iy in 1:nky
ky = kylist[iy]
for ix in 1:nkx
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1]
wmu = zeros(ComplexF64,hn,nkx)
for ix in 1:nkx
kx = kxlist[ix]
wann_v1, wann_v2 = Wilson_kx(kx,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,ix] = wave[:,1,ix] * wann_v1[1] + wave[:,2,ix] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nkx] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for ix in 1:nkx - 1
F0 = wmu[:,ix]' * wmu[:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
pmu = log(wan)/(2*im*pi)
if real(pmu) < 0
pmu += 1
end
pmulist[iy] = pmu
end
return kylist,pmulist
end
可以看到这里对最外层的循环使用了@sync @distributed这个宏定义,但是还需要逐一这里存储结果的数组需要时共享数组1
pmulist = SharedArray(zeros(Float64,nkx))
以上就是julia需要并行所执行的一些操作,最后执行程序1
julia -p 16 file.jl
这里就选择了16个线程进行并行计算。
通过与BBH Nested Wilson loop计算(Julia Version)中的串行执行的程序进行比较,结果如下1
2
3
4
5
6
7
8
9
10
11
12======== Job starts at 2022-03-26 11:04:58 on c07 ========
Nested-BBH 串行检测
203.983876 seconds (419.58 M allocations: 107.249 GiB, 2.55% gc time, 0.09% compilation time)
======== Job ends at 2022-03-26 11:08:28 on c07 ========
======== Job starts at 2022-03-26 11:05:39 on c05 ========
Nested-BBH 并行检测
23.892738 seconds (1.88 M allocations: 104.246 MiB, 0.20% gc time, 3.89% compilation time)
======== Job ends at 2022-03-26 11:06:35 on c05 ========
绘图程序
因为julia绘图不是很好看,所以这里就用python画图了,给一个绘图脚本1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------
def scatterplot1(cont):
da1 = "Nested-kx-" + str(cont) + ".dat"
da2 = "Nested-ky-" + str(cont) + ".dat"
picname = "Nested-" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
with open(da1) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
y0 = np.array(y0)
plt.scatter(x0, y0, s = 20, color = 'lightskyblue', label = "$p_y^{v_x^\pm}(k_x)$")
x1 = []
y1 = []
with open(da2) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x1.append(ldos[0])
y1.append(ldos[1])
y1 = np.array(y1)
# print(y0)
# sc = plt.scatter(x0, y0, c = z1, s = 2,vmin = 0, vmax = 1, cmap="magma")
plt.scatter(x1, y1, s = 20, color = 'deeppink', label = "$p_x^{v_y^\pm}(k_y)$")
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 25,
}
plt.xlim(0,1)
plt.ylim(-1,1)
plt.xlabel("$k_x(k_y)/\pi$",font2)
# plt.ylabel("",font2)
plt.yticks([-1,-0.5,0.,0.5,1],fontproperties='Times New Roman', size = 25)
plt.xticks([-1,0,1],fontproperties='Times New Roman', size = 25)
plt.legend(loc = 'upper left', bbox_to_anchor=(0.5,0.5), shadow = True, prop = font2, markerscale = 4)
# plt.text(x = 0.6,y = 0.7,s = 'MCM', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.text(x = 0.1,y = 0.7,s = 'NSC', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.vlines(x = 0.4, ymin = -1, ymax = 1,lw = 3.0, colors = 'black', linestyles = '--')
plt.savefig(picname, dpi = 600, bbox_inches = 'tight')
#---------------------------------------------------------
def main():
for i0 in range(1,2):
scatterplot1(i0)
#---------------------------------------------------------
if __name__=="__main__":
main()
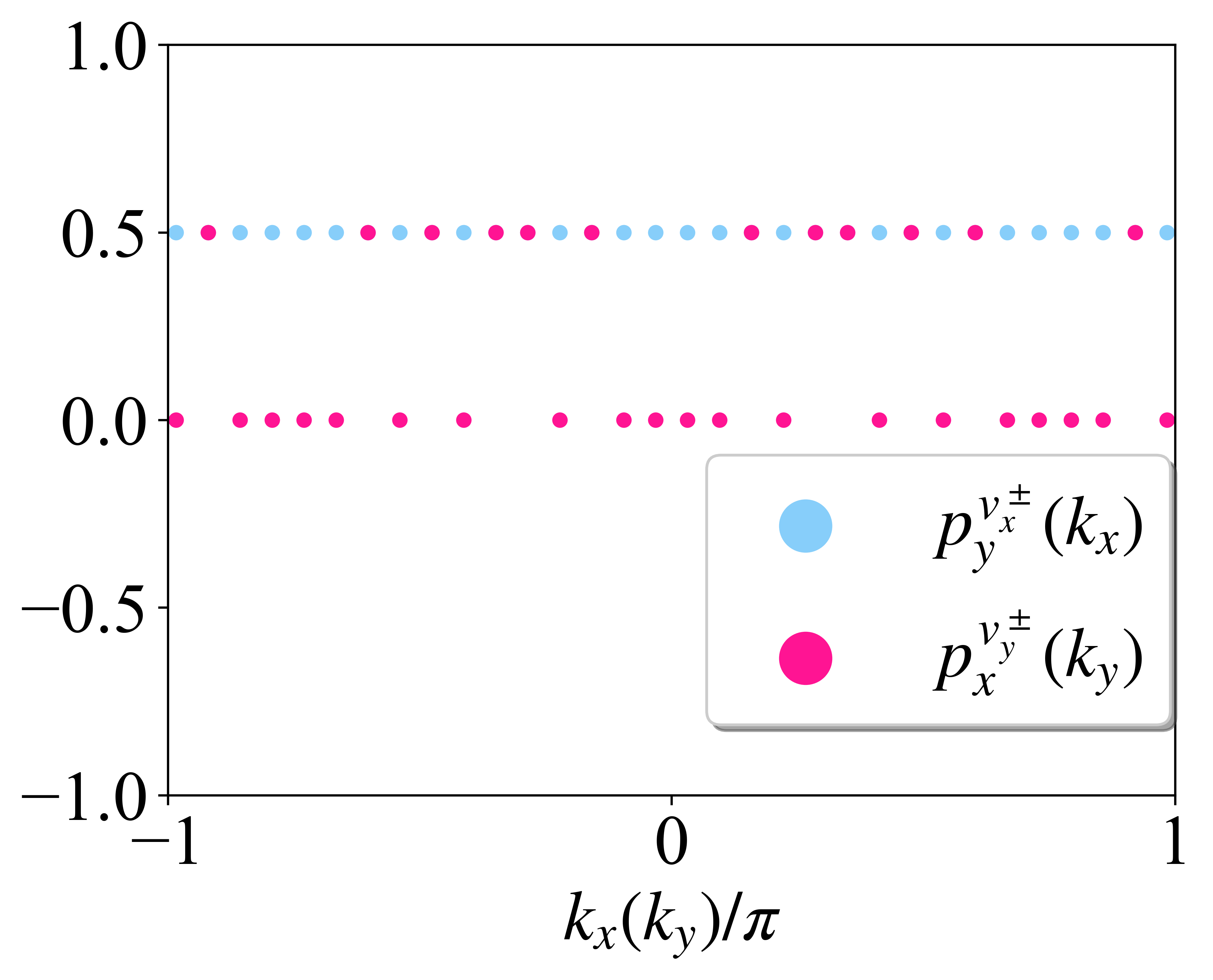
通用版
上面写的程序其实只能用于BBH这一个模型,有点局限。因为要计算Nested Wilson loop其实最终是要对Wannier sector中的每一个Wannier
能带都要计算的,而对于BBH模型来说正好Wannier sector中只有一个能带,所以在构建新的Wannier basis的时候它其实也是一个数,如果一个Wannier sector中有多条Wannier 能带,那么此时就会有多个Wannier basis,在利用新的Wannier basis构建Wilson loop的时候其实就会是一个矩阵,这里就
general的考虑这种情况。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249using DelimitedFiles
using ProgressMeter
using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
#----------------------------------------------------------------------------------------
function hamset(kx::Float64,ky::Float64,m0::Float64,matnum::Int64)::Matrix{ComplexF64}
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.0
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
#--------------------------------------------------------------------------------------
function Wilson_kx(kx::Float64,m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1] # 获取哈密顿量矩阵的维度
Nocc::Int64 = Int(hn/2) # 确定占据态的数量
wave = zeros(ComplexF64,hn,hn,nk) # 存储哈密顿量对应的波函数
wan = zeros(ComplexF64,Nocc,Nocc) # 存储哈密顿量波函数的交叠积分
F = zeros(ComplexF64,Nocc,Nocc) # 计算Wilson loop中的交叠矩阵
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2 * pi, length = nk)
for iy in 1:nk # 固定kx,沿着ky方向计算Wilson loop
ky = klist[iy]
val,vec = eigen(hamset(kx,ky,m0,matnum))
wave[:,:,iy] = vec[:,:] # 存储波函数
end
wave[:,:,nk] = wave[:,:,1] # 在边界上波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1 # 构建单位矩阵
end
for i1 in 1:nk - 1 # index ki lattice
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
# sv1 = svd(wan)
# wan = sv1.U * sv1.Vt #奇异值分解计算交叠矩阵积分
F = wan * F # 沿着ky方向构造Wannier哈密顿量
end
val,vec = eigen(F) # 对求解得到的本征矢量按照本征值大小排列
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 按照顺序对本征态进行排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态(排序后的结果)
# return vec # 给出所有Wannier 本征值对应的本征态
end
#-------------------------------------------------------------------------------------
function Wilson_ky(ky::Float64,m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1]
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nk)
wan = zeros(ComplexF64,Nocc,Nocc)
F = zeros(ComplexF64,Nocc,Nocc)
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2*pi, length = nk)
for ix in 1:nk # 固定ky,沿着kx方向计算Wilson loop
kx = klist[ix]
val,vec = eigen(hamset(kx,ky,m0,matnum))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1
end
for i1 in 1:nk - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
# sv1 = svd(wan)
# wan = sv1.U * sv1.Vt
F = wan * F # 构造Wannier 哈密顿量
end
val,vec = eigen(F) # 对求解得到的本征矢量按照本征值大小排列
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 按照顺序对本征态进行排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态
end
#------------------------------------------------------------------------------------
function Nseted_Wilson_loop_kx(m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
nk::Int64 = nk
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
klist = range(-pi, pi, length = nk)
wave = zeros(ComplexF64,hn,hn,nk)
pmulist = SharedArray(zeros(Float64,nk,Int(Nocc/2)))
for ix in 1:nk # 计算沿着kx方向的Wilson loop
kx = klist[ix]
for iy in 1:nk # 首先在固定kx时,沿着ky方向计算哈密顿量的本征波函数
ky = klist[iy]
val,vec = eigen(hamset(kx,ky,m0,matnum)) # 计算哈密顿量对应的本征矢量
wave[:,:,iy] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
wmu = zeros(ComplexF64,Int(Nocc/2),hn,nk) # 用来构建新的Wannier basis
for i3 in 1:Int(Nocc/2) # 遍历Wannier sector中的每一个Wannier 能带
for iy in 1:nk # 遍历k点
ky = klist[iy]
wann_vec = Wilson_ky(ky,m0,nk,matnum) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
for i4 in 1:Nocc
wmu[i3,:,iy] += wave[:,i4,iy]*wann_vec[i4,i3]
# wmu[i3,:,iy] = wave[:,1,iy] * wann_vec[1,i3] + wave[:,2,iy] * wann_vec[2,i3] + wave[:,3,iy] * wann_vec[3,i3] + wave[:,4,iy] * wann_vec[4,i3] # 构建新的Wannier basis
end
end
wmu[i3,:,nk] = wmu[i3,:,1] # 首尾相接
end
# 在新的形式下构建Wilson loop
wan = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2)) # 对确定的Wannier sector中的每一个Wannier 能带计算Wilson loop
F0 = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2))
for i4 in 1:Int(Nocc/2)
wan[i4,i4] = 1
end
for iy in 1:nk - 1
for i3 in 1:Int(Nocc/2)
for i2 in 1:Int(Nocc/2)
F0[i3,i2] = wmu[i3,:,iy]' * wmu[i2,:,iy + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
end
end
# sv1 = svd(F0)
# F0 = sv1.U * sv1.Vt
wan = F0 * wan
end
val,vec = eigen(wan) # 利用新基矢构建出来的Wilson loop
pmu = map(angle,val)/(2 * pi)
for i0 in 1:length(pmu)
if pmu[i0] < 0
pmu[i0] += 1
end
end
pmulist[ix,:] = pmu
end
return klist,pmulist
end
#-----------------------------------------------------------------------
function Nseted_Wilson_loop_ky(m0::Float64,nk::Int64,matnum::Int64)
# nk = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1]
Nocc::Int64 = Int(hn/2)
klist = range(-pi,pi,length = nk)
wave = zeros(ComplexF64,hn,hn,nk) # 哈密顿量波函数
pmulist = SharedArray(zeros(Float64,nk,Int(Nocc/2)))
for iy in 1:nk
ky = klist[iy]
for ix in 1:nk
kx = klist[ix]
val,vec = eigen(hamset(kx,ky,m0,matnum)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1]
wmu = zeros(ComplexF64,Int(Nocc/2),hn,nk) # 用来构建新的Wannier basis
for i3 in 1:Int(Nocc/2) # 遍历Wannier sector中的每一个Wannier 能带
for ix in 1:nk # 遍历k点
kx = klist[ix]
wann_vec = Wilson_kx(kx,m0,nk,matnum) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
for i4 in 1:Nocc
wmu[i3,:,ix] += wave[:,i4,ix]*wann_vec[i4,i3]
end
end
wmu[i3,:,nk] = wmu[i3,:,1] # 首尾相接
end
# 在新的形式下构建Wilson loop
wan = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2)) # 对确定的Wannier sector中的每一个Wannier 能带计算Wilson loop
F0 = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2))
for i4 in 1:Int(Nocc/2)
wan[i4,i4] = 1
end
for ix in 1:nk - 1
for i3 in 1:Int(Nocc/2)
for i2 in 1:Int(Nocc/2)
F0[i3,i2] = wmu[i3,:,ix]' * wmu[i2,:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
end
end
# sv1 = svd(F0)
# F0 = sv1.U * sv1.Vt
wan = F0 * wan
end
val,vec = eigen(wan)
pmu = map(angle,val)/(2 * pi)
for i0 in 1:length(pmu)
if pmu[i0] < 0
pmu[i0] += 1
end
end
pmulist[iy,:] = pmu
end
return klist,pmulist
end
#----------------------------------------------------------------------------------------------
function Nested(m0::Float64,nk::Int64,matnum::Int64)
x1,x2 = Nseted_Wilson_loop_ky(m0,nk,matnum)
x3,x4 = Nseted_Wilson_loop_kx(m0,nk,matnum)
re1 = 0
re2 = 0
for i0 in 1:length(x1)
re1 += mod(sum(x2[i0,:]),1)# 对同一个Wannier sector中的两个Wannier band求和
re2 += mod(sum(x4[i0,:]),1)# 对同一个Wannier sector中的两个Wannier band求和
end
re1 = re1/length(x1)
re2 = re2/length(x1)
return re1,re2,2*re1*re2
end
#---------------------------------------------------------------------
function main()
# 测试增加k点结果是否收敛(主要是以BBH模型为测试基准)
i0::Int64 = 1
nklist = 20:10:100
relist = zeros(Float64,length(nklist),3)
m0::Float64 = 1.0
matnum::Int64 = 1
for nk in nklist
re1,re2,re3 = Nested(m0,nk,matnum)
relist[i0,:] = [re1 re2 re3]
i0 += 1
end
# fx1 = "-polar-" * string(num) * ".dat"
fx1 ="polar-all.dat"
f1 = open(fx1,"w")
writedlm(f1,[nklist relist],"\t")
close(f1)
end
#--------------------------------------------------------------------------
main()
这里是执行了一个收敛性测试,看看随着$k$点数目的增加,结果是否是稳定不变的。
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |









