这里就使用Julia写了一下Nested Wilson loop的并行程序,因为前面考虑的体系其实就是一个$4\times 4$的哈密顿量,如果体系变大以及计算撒点数量变大的时候,julia还是会有点慢,这里就给一个并行的版本,并顺便看一下julia是怎么并行的。
Nested Wilson Loop
关于Nested Wilson loop的计算可以参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators 这篇文章,这里主要说一下自己在学习计算的时候踩过的坑。
与计算Wilson loop相同,这里最主要的仍然是找到一个Wannier band basis,也就是文章的中的公式
\[\rvert w_{x,\mathbf{k}}^j\rangle=\sum_{n=1}^\text{Nocc}\rvert u^n_\mathbf{k}\rangle[v_{x,\mathbf{k}}^j]^n\]其实在做计算的时候,最让人困扰的不过是公式中的一大堆符号对应的到底是什么,这里就来讲这个公式拆解开,一步一步的讲清楚里面的含义。这里假设你已经知道为什么要计算Nested Wilson loop, 我在这里就简单的阐述一下。首先要是体系的Wilson loop计算对应的Wannier哈密顿量的能带是有能隙的,也就是说你的体系是4带模型,那么当占据态是2条能带的时候,每个占据态能带会对应着一个Wannier center, 比如BHZ模型的两条占据态能带对应的Wannier band就是相互交叉的,而且因为Wilson loop与边界态之间的拓扑等价性,TI是有边界态的,所以其对应的Wilson loop在形状上就与边界态类似。而对于高阶拓扑相, 首先就是要使得边界态打开能隙,那么相对应的就是其Wilson loop计算得到的Wannier center随着某个动量参数的演化是不会相互交叉的,这一点在上面BBH模型中已经计算过了,所以此时就可以对某一个单独的Wannier band 计算它的Nested Wilson loop,所以首先第一步就是必须要明白什么样的情况下,是需要计算体系的Nested Wilson loop。
这里的$\sum_{n=1}^\text{Nocc}$不用讲太多,是需要对占据态进行求和,但是这个$n$其实表示的只是说哈密顿量的占据态,也就是说对于$\rvert u^n_\mathbf{k}\rangle$而言,这是哈密顿量的占据态波函数,$n$表示占据态其实是对$\rvert u^n_\mathbf{k}\rangle$ 而言的,虽然$[v_{x,\mathbf{k}}^j]^n$中同样存在这个$n$,但是在这个地方$n$代表的不是占据态,在这里$j$代表的才是你选择的是哪一个Wannier band来计算其对应的Nested Wilson loop,也就是这里$j$代表的是你选择的是那个占据的Wannier band,而$n$在这里 表示的是一个Wannier哈密顿量本征矢量的第$n$个分量。假如$H_\text{Wann}$是Wannier哈密顿量,其满足
\[H_\text{Wann}\rvert v_\mathbf{k}\rangle=E\rvert v_\mathbf{k}\rangle\]那么这里的$[v_{x,\mathbf{k}}^j]^n$表示的就是这个本征矢量的第$n$个分量,$j$则表示你选择是哪个本征值对应的本征矢量,也就是选择了哪一个Wannier band。这里的$x$则表示你在做Wilson loop的时候,是沿着哪个方向进行的,即就是讲上面公式中的$H_\text{Wann}$替换成你 构建的那个Wilson loop的哈密顿量就可以。
至于$\rvert u^n_\mathbf{k}\rangle$就很简单了,它表示的就是你的哈密顿量的本征态,当然了在计算的时候,还是要选择正确的占据态才可以。下面直接上代码,在其中同样做了注释
using DelimitedFiles
using ProgressMeter
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
#--------------------------------------------------------------
@everywhere function hamset(kx::Float64,ky::Float64)
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.000000000000
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
#--------------------------------------------------------------------------------------
@everywhere function Wilson_kx(kx::Float64,nky::Int64)
# nky::Int64 = 100
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nky) # 存储哈密顿量对应的波函数
wan = zeros(ComplexF64,Nocc,Nocc) # 存储Wannier哈密顿量对应的波函数
F = zeros(ComplexF64,Nocc,Nocc)
kylist = range(0, 2*pi, length = nky)
for iy in 1:nky # 固定kx,沿着ky方向计算Wilson loop
ky = kylist[iy]
val,vec = eigen(hamset(kx,ky))
wave[:,:,iy] = vec[:,:] # 存储波函数
end
wave[:,:,nky] = wave[:,:,1] # 在边界上波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1 # 构建单位矩阵
end
for i1 in 1:nky - 1 # index ki lattice
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
F = wan * F # 沿着ky方向构造Wannier哈密顿量
end
val,vec = eigen(F) # 这里求解得到的本征态是按照本征值的大小进行排列的,和python有一点不同
vec1 = vec[:,sortperm(map(angle,val))[1]]
vec2 = vec[:,sortperm(map(angle,val))[2]]
return vec1,vec2# 给出两个占据态能带对应的Wannier哈密顿量的本征矢量
end
#-------------------------------------------------------------------------------------
@everywhere function Wilson_ky(ky::Float64,nkx::Int64)
# nkx::Int64 = 100
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nkx)
wan = zeros(ComplexF64,Nocc,Nocc)
F = zeros(ComplexF64,Nocc,Nocc)
kxlist = range(0, 2*pi, length = nkx)
for ix in 1:nkx # 固定ky,沿着kx方向计算Wilson loop
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1
end
for i1 in 1:nkx - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
F = wan * F # 构造Wannier 哈密顿量
end
val,vec = eigen(F)
vec1 = vec[:,sortperm(map(angle,val))[1]]
vec2 = vec[:,sortperm(map(angle,val))[2]]
return vec1,vec2# 给出两个占据态能带对应的Wannier哈密顿量的本征矢量
# return sort(map(angle,val)/(2*pi))
end
#------------------------------------------------------------------------------------
@everywhere function Nseted_Wilson_loop_kx(nkx::Int64)
# nkx::Int64 = 100
nky::Int64 = nkx
hn::Int64 = 4
Nocc::Int64 = Int(hn/2)
kxlist = range(-pi, pi, length = nkx)
kylist = range(-pi, pi, length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
@sync @distributed for ix in 1:nkx
kx = kxlist[ix]
for iy in 1:nky
ky = kylist[iy]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,iy] = vec[:,:]
end
wave[:,:,nky] = wave[:,:,1] # 波函数首尾相接
wmu = zeros(ComplexF64,hn,nky) # 用来构建新的Wannier basis
for iy in 1:nky
ky = kylist[iy]
wann_v1, wann_v2 = Wilson_ky(ky,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,iy] = wave[:,1,iy] * wann_v1[1] + wave[:,2,iy] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nky] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for iy in 1:nky - 1
F0 = wmu[:, iy]' * wmu[:, iy + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
#pmu = log(wan)/(2 * im * pi)
pmu = map(angle,wan)/(2*pi)
if pmu < 0
pmu += 1
end
pmulist[ix] = pmu
end
return kylist,pmulist
end
#-----------------------------------------------------------------------
@everywhere function Nseted_Wilson_loop_ky(nkx::Int64)
# nkx = 100
nky = nkx
hn = 4
Nocc = Int(hn/2)
kxlist = range(-pi,pi,length = nkx)
kylist = range(-pi,pi,length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
@sync @distributed for iy in 1:nky
ky = kylist[iy]
for ix in 1:nkx
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1]
wmu = zeros(ComplexF64,hn,nkx)
for ix in 1:nkx
kx = kxlist[ix]
wann_v1, wann_v2 = Wilson_kx(kx,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,ix] = wave[:,1,ix] * wann_v1[1] + wave[:,2,ix] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nkx] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for ix in 1:nkx - 1
F0 = wmu[:,ix]' * wmu[:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
#pmu = log(wan)/(2*im*pi)
pmu = map(angle,wan)/(2*pi)
if pmu < 0
pmu += 1
end
pmulist[iy] = pmu
end
return kylist,pmulist
end
#----------------------------------------------------------------------------------------------
function Nested(num)
nkx = 100
x1,x2 = Nseted_Wilson_loop_ky(nkx)
fx1 = "Nested-ky-" * string(num) * ".dat"
f1 = open(fx1,"w")
writedlm(f1,[x1 x2],"\t")
close(f1)
x1,x2 = Nseted_Wilson_loop_kx(nkx)
fx1 = "Nested-kx-" * string(num) * ".dat"
f1 = open(fx1,"w")
writedlm(f1,[x1 x2],"\t")
close(f1)
end
#-----------------------------------------------------------------
# @time test()
@time Nested(1)
Julia并行
其实对于julia来说,并行还是还是非常方便的,首先加入几个函数库
using DelimitedFiles
using ProgressMeter
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
这里使用@everywhere是为了让每个线程都可以看到这些库函数,接下来就是要对需要并行的函数,每个函数前面也都加入@everywhere。
@everywhere function hamset(kx::Float64,ky::Float64)
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.000000000000
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
最后一步就是需要对需要并行计算的循环进行修改
@everywhere function Nseted_Wilson_loop_ky(nkx::Int64)
# nkx = 100
nky = nkx
hn = 4
Nocc = Int(hn/2)
kxlist = range(-pi,pi,length = nkx)
kylist = range(-pi,pi,length = nky)
wave = zeros(ComplexF64,hn,hn,nky)
pmulist = SharedArray(zeros(Float64,nkx))
@sync @distributed for iy in 1:nky
ky = kylist[iy]
for ix in 1:nkx
kx = kxlist[ix]
val,vec = eigen(hamset(kx,ky)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nkx] = wave[:,:,1]
wmu = zeros(ComplexF64,hn,nkx)
for ix in 1:nkx
kx = kxlist[ix]
wann_v1, wann_v2 = Wilson_kx(kx,nkx) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
wmu[:,ix] = wave[:,1,ix] * wann_v1[1] + wave[:,2,ix] * wann_v1[2] # 构建新的Wannier basis
end
wmu[:,nkx] = wmu[:,1] # 首尾相接
# 在新的形式下构建Wilson loop
wan = 1
for ix in 1:nkx - 1
F0 = wmu[:,ix]' * wmu[:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
wan = F0 * wan
end
pmu = log(wan)/(2*im*pi)
if real(pmu) < 0
pmu += 1
end
pmulist[iy] = pmu
end
return kylist,pmulist
end
可以看到这里对最外层的循环使用了@sync @distributed这个宏定义,但是还需要逐一这里存储结果的数组需要时共享数组
pmulist = SharedArray(zeros(Float64,nkx))
以上就是julia需要并行所执行的一些操作,最后执行程序
julia -p 16 file.jl
这里就选择了16个线程进行并行计算。
通过与BBH Nested Wilson loop计算(Julia Version)中的串行执行的程序进行比较,结果如下
======== Job starts at 2022-03-26 11:04:58 on c07 ========
Nested-BBH 串行检测
203.983876 seconds (419.58 M allocations: 107.249 GiB, 2.55% gc time, 0.09% compilation time)
======== Job ends at 2022-03-26 11:08:28 on c07 ========
======== Job starts at 2022-03-26 11:05:39 on c05 ========
Nested-BBH 并行检测
23.892738 seconds (1.88 M allocations: 104.246 MiB, 0.20% gc time, 3.89% compilation time)
======== Job ends at 2022-03-26 11:06:35 on c05 ========
绘图程序
因为julia绘图不是很好看,所以这里就用python画图了,给一个绘图脚本
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------
def scatterplot1(cont):
da1 = "Nested-kx-" + str(cont) + ".dat"
da2 = "Nested-ky-" + str(cont) + ".dat"
picname = "Nested-" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
with open(da1) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
y0 = np.array(y0)
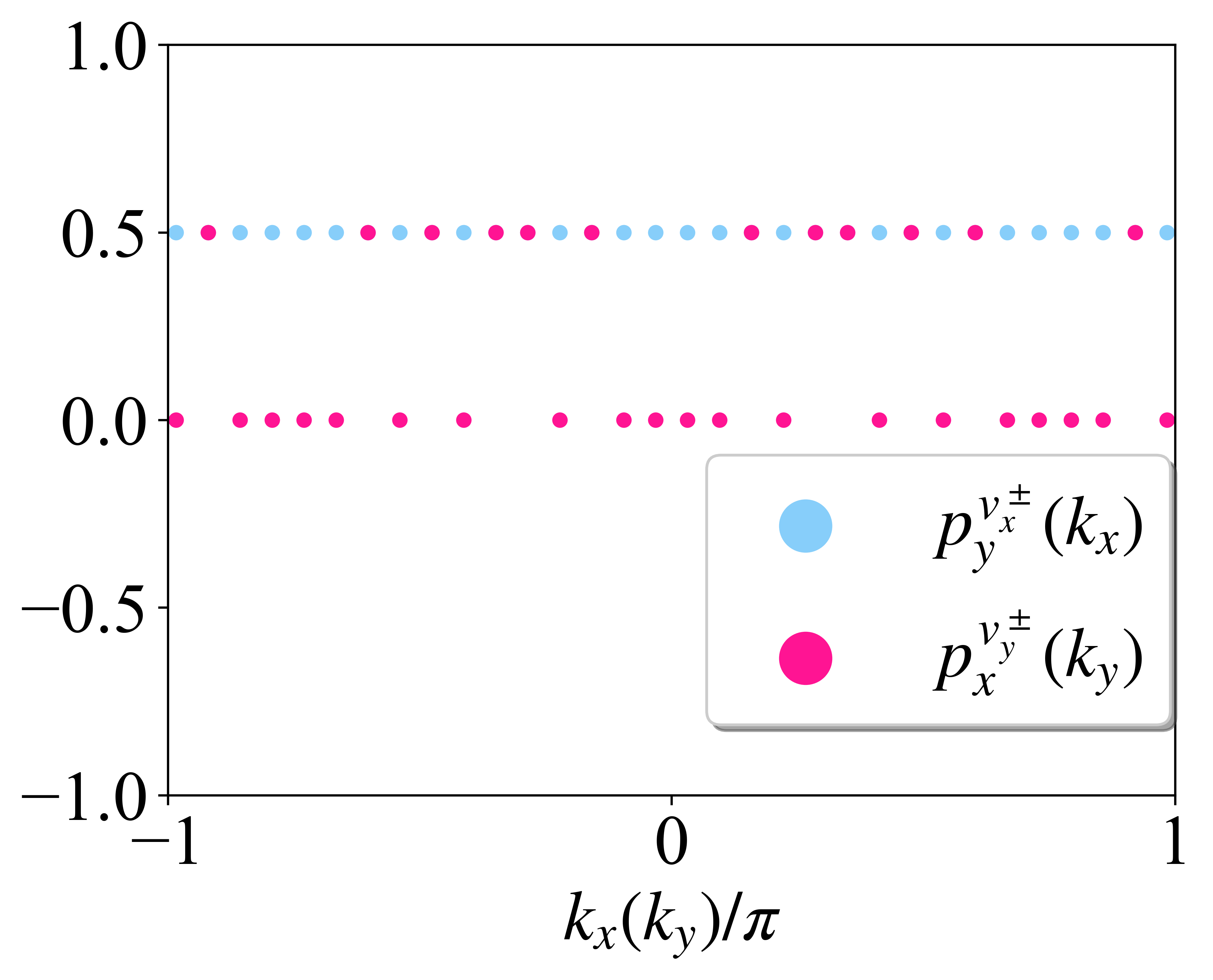
plt.scatter(x0, y0, s = 20, color = 'lightskyblue', label = "$p_y^{v_x^\pm}(k_x)$")
x1 = []
y1 = []
with open(da2) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x1.append(ldos[0])
y1.append(ldos[1])
y1 = np.array(y1)
# print(y0)
# sc = plt.scatter(x0, y0, c = z1, s = 2,vmin = 0, vmax = 1, cmap="magma")
plt.scatter(x1, y1, s = 20, color = 'deeppink', label = "$p_x^{v_y^\pm}(k_y)$")
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 25,
}
plt.xlim(0,1)
plt.ylim(-1,1)
plt.xlabel("$k_x(k_y)/\pi$",font2)
# plt.ylabel("",font2)
plt.yticks([-1,-0.5,0.,0.5,1],fontproperties='Times New Roman', size = 25)
plt.xticks([-1,0,1],fontproperties='Times New Roman', size = 25)
plt.legend(loc = 'upper left', bbox_to_anchor=(0.5,0.5), shadow = True, prop = font2, markerscale = 4)
# plt.text(x = 0.6,y = 0.7,s = 'MCM', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.text(x = 0.1,y = 0.7,s = 'NSC', fontdict=dict(fontsize=20, color='black',family='Times New Roman'))
# plt.vlines(x = 0.4, ymin = -1, ymax = 1,lw = 3.0, colors = 'black', linestyles = '--')
plt.savefig(picname, dpi = 600, bbox_inches = 'tight')
#---------------------------------------------------------
def main():
for i0 in range(1,2):
scatterplot1(i0)
#---------------------------------------------------------
if __name__=="__main__":
main()
通用版
上面写的程序其实只能用于BBH这一个模型,有点局限。因为要计算Nested Wilson loop其实最终是要对Wannier sector中的每一个Wannier
能带都要计算的,而对于BBH模型来说正好Wannier sector中只有一个能带,所以在构建新的Wannier basis的时候它其实也是一个数,如果一个
Wannier sector中有多条Wannier 能带,那么此时就会有多个Wannier basis,在利用新的Wannier basis构建Wilson loop的时候其实就会是一个矩阵,这里就
general的考虑这种情况。
using DelimitedFiles
using ProgressMeter
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
#----------------------------------------------------------------------------------------
@everywhere function hamset(kx::Float64,ky::Float64,m0::Float64,matnum::Int64)::Matrix{ComplexF64}
hn::Int64 = 4
gamx::Float64 = 0.5
lamx::Float64 = 1.0
gamy::Float64 = gamx
lamy::Float64 = lamx
xsyb1::Float64 = 0.000000000000
xsyb2::Float64 = 1.1
ysyb1::Float64 = 0.000000000000
ysyb2::Float64 = 1.0
ham = zeros(ComplexF64, hn, hn)
ham[1, 1] = xsyb1
ham[2, 2] = ysyb1
ham[3, 3] = ysyb1
ham[4, 4] = xsyb1
ham[1, 3] = (gamx + lamx * exp(im * kx)) * ysyb2
ham[2, 4] = gamx + lamx * exp(-im * kx)
ham[1, 4] = gamy + lamy * exp(im * ky)
ham[2, 3] = (-gamy - lamy * exp(-im * ky)) * xsyb2
ham[3, 1] = conj(ham[1, 3])
ham[4, 2] = conj(ham[2, 4])
ham[4, 1] = conj(ham[1, 4])
ham[3, 2] = conj(ham[2, 3])
return ham
end
#--------------------------------------------------------------------------------------
@everywhere function Wilson_kx(kx::Float64,m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1] # 获取哈密顿量矩阵的维度
Nocc::Int64 = Int(hn/2) # 确定占据态的数量
wave = zeros(ComplexF64,hn,hn,nk) # 存储哈密顿量对应的波函数
wan = zeros(ComplexF64,Nocc,Nocc) # 存储哈密顿量波函数的交叠积分
F = zeros(ComplexF64,Nocc,Nocc) # 计算Wilson loop中的交叠矩阵
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2 * pi, length = nk)
for iy in 1:nk # 固定kx,沿着ky方向计算Wilson loop
ky = klist[iy]
val,vec = eigen(hamset(kx,ky,m0,matnum))
wave[:,:,iy] = vec[:,:] # 存储波函数
end
wave[:,:,nk] = wave[:,:,1] # 在边界上波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1 # 构建单位矩阵
end
for i1 in 1:nk - 1 # index ki lattice
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
# sv1 = svd(wan)
# wan = sv1.U * sv1.Vt #奇异值分解计算交叠矩阵积分
F = wan * F # 沿着ky方向构造Wannier哈密顿量
end
val,vec = eigen(F) # 对求解得到的本征矢量按照本征值大小排列
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 按照顺序对本征态进行排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态(排序后的结果)
# return vec # 给出所有Wannier 本征值对应的本征态
end
#-------------------------------------------------------------------------------------
@everywhere function Wilson_ky(ky::Float64,m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1]
Nocc::Int64 = Int(hn/2)
wave = zeros(ComplexF64,hn,hn,nk)
wan = zeros(ComplexF64,Nocc,Nocc)
F = zeros(ComplexF64,Nocc,Nocc)
vec2 = zeros(ComplexF64,Nocc,Nocc) # 重新排列顺序后Wannier Hamiltonian的本征矢量
klist = range(0, 2*pi, length = nk)
for ix in 1:nk # 固定ky,沿着kx方向计算Wilson loop
kx = klist[ix]
val,vec = eigen(hamset(kx,ky,m0,matnum))
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
for i1 in 1:Nocc
F[i1,i1] = 1
end
for i1 in 1:nk - 1
for i2 in 1:Nocc
for i3 in 1:Nocc
wan[i2,i3] = wave[:,i2,i1]' * wave[:,i3,i1 + 1] # 计算Berry联络
end
end
# sv1 = svd(wan)
# wan = sv1.U * sv1.Vt
F = wan * F # 构造Wannier 哈密顿量
end
val,vec = eigen(F) # 对求解得到的本征矢量按照本征值大小排列
for i0 in 1:Nocc
vec2[:,i0] = vec[:,sortperm(map(angle,val))[i0]] # 按照顺序对本征态进行排列
end
return vec2 # 给出所有Wannier 本征值对应的本征态
end
#------------------------------------------------------------------------------------
@everywhere function Nseted_Wilson_loop_kx(m0::Float64,nk::Int64,matnum::Int64)
# nk::Int64 = 100
nk::Int64 = nk
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1] # 直接通过哈密顿量来获取其维度,程序具有通用性
Nocc::Int64 = Int(hn/2) # 获取占据态的数量
klist = range(-pi, pi, length = nk)
wave = zeros(ComplexF64,hn,hn,nk)
pmulist = SharedArray(zeros(Float64,nk,Int(Nocc/2)))
@sync @distributed for ix in 1:nk # 计算沿着kx方向的Wilson loop
kx = klist[ix]
for iy in 1:nk # 首先在固定kx时,沿着ky方向计算哈密顿量的本征波函数
ky = klist[iy]
val,vec = eigen(hamset(kx,ky,m0,matnum)) # 计算哈密顿量对应的本征矢量
wave[:,:,iy] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1] # 波函数首尾相接
wmu = zeros(ComplexF64,Int(Nocc/2),hn,nk) # 用来构建新的Wannier basis
for i3 in 1:Int(Nocc/2) # 遍历Wannier sector中的每一个Wannier 能带
for iy in 1:nk # 遍历k点
ky = klist[iy]
wann_vec = Wilson_ky(ky,m0,nk,matnum) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
for i4 in 1:Nocc
wmu[i3,:,iy] += wave[:,i4,iy]*wann_vec[i4,i3]
# wmu[i3,:,iy] = wave[:,1,iy] * wann_vec[1,i3] + wave[:,2,iy] * wann_vec[2,i3] + wave[:,3,iy] * wann_vec[3,i3] + wave[:,4,iy] * wann_vec[4,i3] # 构建新的Wannier basis
end
end
wmu[i3,:,nk] = wmu[i3,:,1] # 首尾相接
end
# 在新的形式下构建Wilson loop
wan = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2)) # 对确定的Wannier sector中的每一个Wannier 能带计算Wilson loop
F0 = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2))
for i4 in 1:Int(Nocc/2)
wan[i4,i4] = 1
end
for iy in 1:nk - 1
for i3 in 1:Int(Nocc/2)
for i2 in 1:Int(Nocc/2)
F0[i3,i2] = wmu[i3,:,iy]' * wmu[i2,:,iy + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
end
end
# sv1 = svd(F0)
# F0 = sv1.U * sv1.Vt
wan = F0 * wan
end
val,vec = eigen(wan) # 利用新基矢构建出来的Wilson loop
pmu = map(angle,val)/(2 * pi)
for i0 in 1:length(pmu)
if pmu[i0] < 0
pmu[i0] += 1
end
end
pmulist[ix,:] = pmu
end
return klist,pmulist
end
#-----------------------------------------------------------------------
@everywhere function Nseted_Wilson_loop_ky(m0::Float64,nk::Int64,matnum::Int64)
# nk = 100
hn::Int64 = size(hamset(0.0,0.0,m0,matnum))[1]
Nocc::Int64 = Int(hn/2)
klist = range(-pi,pi,length = nk)
wave = zeros(ComplexF64,hn,hn,nk) # 哈密顿量波函数
pmulist = SharedArray(zeros(Float64,nk,Int(Nocc/2)))
@sync @distributed for iy in 1:nk
ky = klist[iy]
for ix in 1:nk
kx = klist[ix]
val,vec = eigen(hamset(kx,ky,m0,matnum)) # 计算哈密顿量对应的本征矢量
wave[:,:,ix] = vec[:,:]
end
wave[:,:,nk] = wave[:,:,1]
wmu = zeros(ComplexF64,Int(Nocc/2),hn,nk) # 用来构建新的Wannier basis
for i3 in 1:Int(Nocc/2) # 遍历Wannier sector中的每一个Wannier 能带
for ix in 1:nk # 遍历k点
kx = klist[ix]
wann_vec = Wilson_kx(kx,m0,nk,matnum) # 在固定ky的情况下,计算沿着kx方向的Wilson loop并得到对应的本征矢量
for i4 in 1:Nocc
wmu[i3,:,ix] += wave[:,i4,ix]*wann_vec[i4,i3]
end
end
wmu[i3,:,nk] = wmu[i3,:,1] # 首尾相接
end
# 在新的形式下构建Wilson loop
wan = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2)) # 对确定的Wannier sector中的每一个Wannier 能带计算Wilson loop
F0 = zeros(ComplexF64,Int(Nocc/2),Int(Nocc/2))
for i4 in 1:Int(Nocc/2)
wan[i4,i4] = 1
end
for ix in 1:nk - 1
for i3 in 1:Int(Nocc/2)
for i2 in 1:Int(Nocc/2)
F0[i3,i2] = wmu[i3,:,ix]' * wmu[i2,:,ix + 1] # 在新的Wannier basis下面构建Wilson loop,也就是计算Nested Wilson loop
end
end
# sv1 = svd(F0)
# F0 = sv1.U * sv1.Vt
wan = F0 * wan
end
val,vec = eigen(wan)
pmu = map(angle,val)/(2 * pi)
for i0 in 1:length(pmu)
if pmu[i0] < 0
pmu[i0] += 1
end
end
pmulist[iy,:] = pmu
end
return klist,pmulist
end
#----------------------------------------------------------------------------------------------
@everywhere function Nested(m0::Float64,nk::Int64,matnum::Int64)
x1,x2 = Nseted_Wilson_loop_ky(m0,nk,matnum)
x3,x4 = Nseted_Wilson_loop_kx(m0,nk,matnum)
re1 = 0
re2 = 0
for i0 in 1:length(x1)
re1 += mod(sum(x2[i0,:]),1)# 对同一个Wannier sector中的两个Wannier band求和
re2 += mod(sum(x4[i0,:]),1)# 对同一个Wannier sector中的两个Wannier band求和
end
re1 = re1/length(x1)
re2 = re2/length(x1)
return re1,re2,2*re1*re2
end
#---------------------------------------------------------------------
function main()
# 测试增加k点结果是否收敛(主要是以BBH模型为测试基准)
i0::Int64 = 1
nklist = 20:10:100
relist = zeros(Float64,length(nklist),3)
m0::Float64 = 1.0
matnum::Int64 = 1
for nk in nklist
re1,re2,re3 = Nested(m0,nk,matnum)
relist[i0,:] = [re1 re2 re3]
i0 += 1
end
# fx1 = "-polar-" * string(num) * ".dat"
fx1 ="polar-all.dat"
f1 = open(fx1,"w")
writedlm(f1,[nklist relist],"\t")
close(f1)
end
#--------------------------------------------------------------------------
@time main()
这里是执行了一个收敛性测试,看看随着$k$点数目的增加,结果是否是稳定不变的。
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |