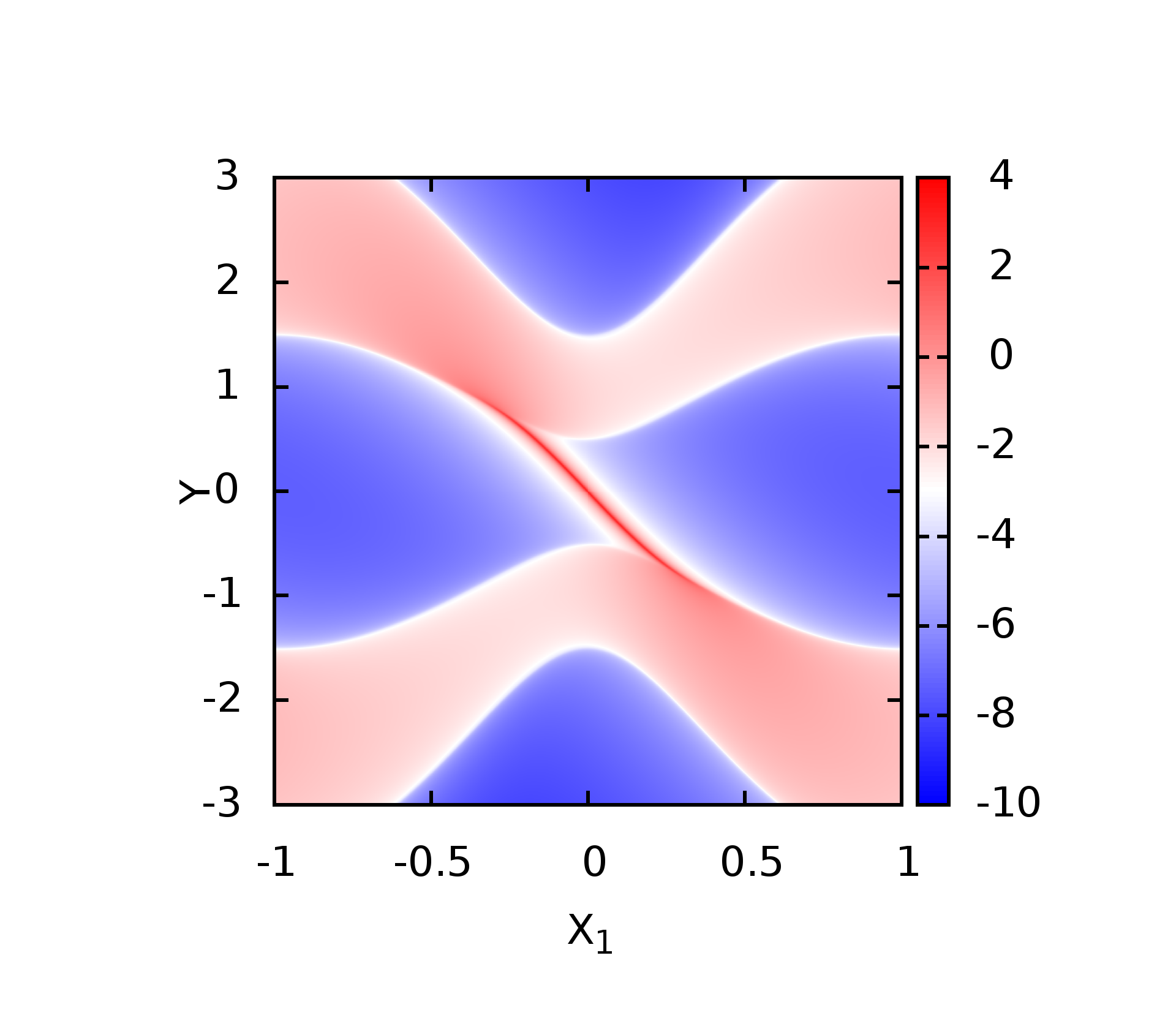
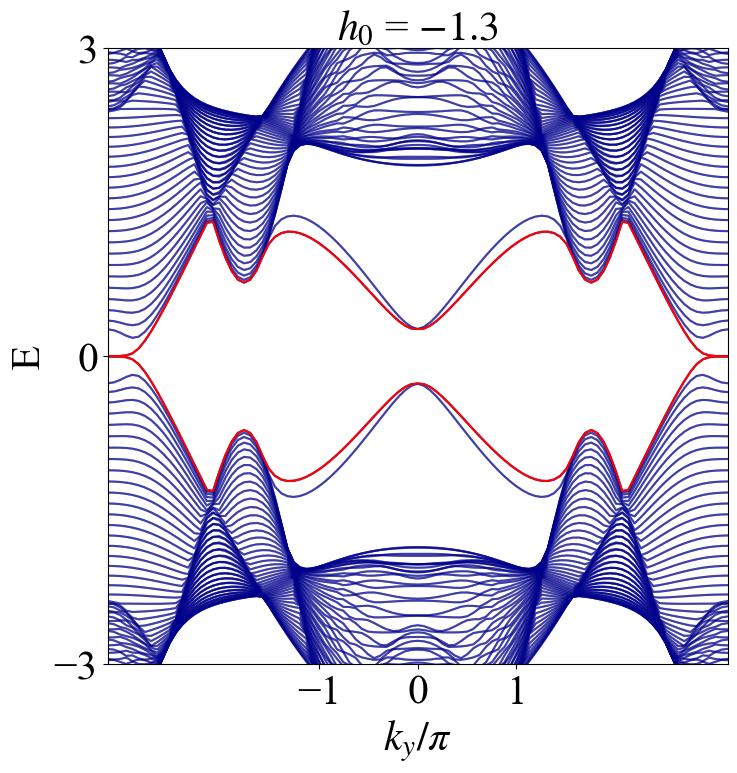
BBH实空间计算
之前其实已经研究过BBH模型的拓扑性质,但是一直没去写实空间电荷分布以及零能态的代码,这里补一下作业。
{:.info}
模型
废话不说,直接给模型上代码,具体的性质可以参考Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators这篇文章。
代码
1 | using ProgressMeter |
绘图
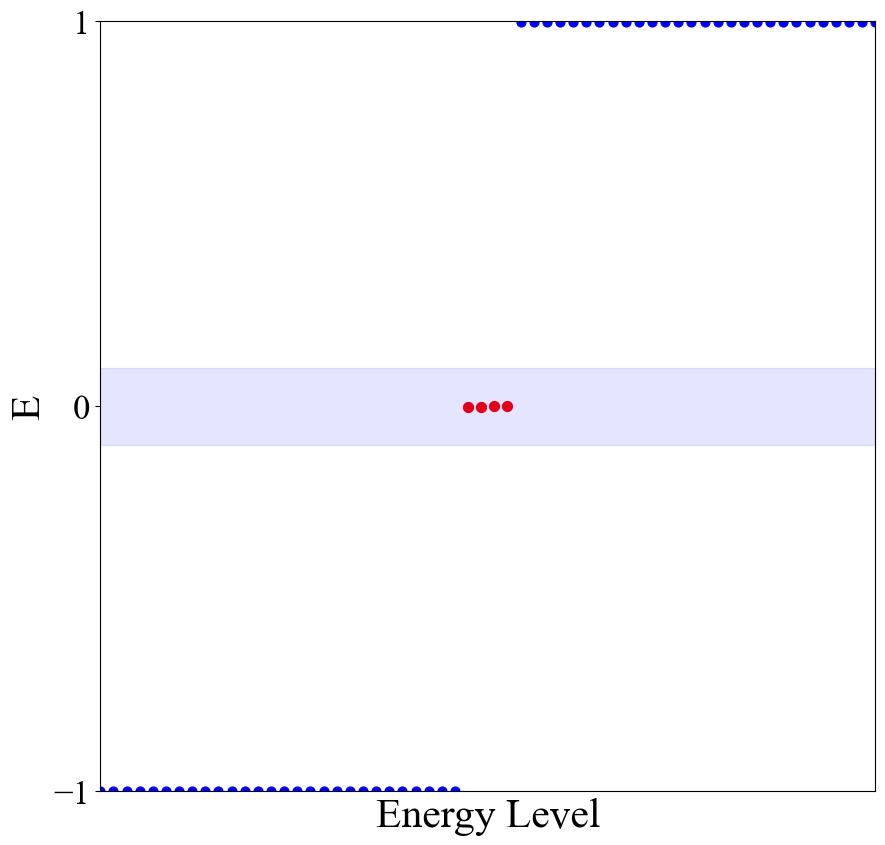
Julia目前画图调整方面我不是很熟悉,所以暂时先用Python作图了。分别给出实空间的本征值,态密度,残余电荷1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146import numpy as np
import matplotlib.pyplot as plt
import os
#---------------------------------------------------------
def ldosplt(cont):
dataname = "m1-ldos-" + str(cont).rjust(2,'0') + ".dat"
dataname = "dos.dat"
picname = "ldos-m1-" + str(cont).rjust(2,'0') + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
z0 = []
z1 = []
with open(dataname) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
z0.append(ldos[2])
z1.append(ldos[3])
z0 = (z0 - np.min(z0))/(np.max(z0) - np.min(z0))*3000 # 数据归一化
plt.figure(figsize=(15, 15))
sc = plt.scatter(x0, y0, c = z0,s = z0,vmin=0, vmax=1,cmap="bwr",edgecolor="black")
cb = plt.colorbar(sc,fraction = 0.045) # 调整colorbar的大小和图之间的间距
cb.ax.tick_params(labelsize = 30)
cb.set_ticks(np.linspace(0,1,2))
cb.set_ticklabels(('0','1.0'))
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 40,
}
cb.set_label('LDOS',fontdict=font2) #设置colorbar的标签字体及其大小
plt.scatter(x0, y0, s = 5, color='blue',edgecolor="blue")
plt.axis('scaled')
plt.xlabel("x",font2)
plt.ylabel("y",font2)
plt.title("Local Density of State",font2)
plt.yticks([0,15,30],fontproperties='Times New Roman', size = 30)
plt.xticks([0,15,30],fontproperties='Times New Roman', size = 30)
plt.savefig(picname, dpi = 100)
plt.close()
#---------------------------------------------------------
def eigval(cont):
dataname = "eigval-m1-" + str(cont).rjust(4,'0') + ".dat"
dataname = "eigval.dat"
picname = "m1-val-" + str(cont).rjust(4,'0') + ".png"
x0 = []
y0 = []
with open(dataname) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 2:
da1 = [float(x) for x in f1.strip().split()]
x0.append(da1[0])
y0.append(da1[1])
# plt.plot(x0, y0)
# plt.title("|C| = 1",size = 20,fontproperties='Times New Roman')
datalen = int(len(x0)/2)
vallen = 30
len1 = int(len(y0)/2)
y0 = y0[len1 - vallen:len1 + vallen]
valmin = np.min(y0)
valmax = np.max(y0)
x0 = range(len(y0))
#----------------------------------
plt.figure(figsize=(10, 10))
sc = plt.scatter(x0, y0, s = 40,c='blue')
sc = plt.scatter(x0[int(len(x0)/2)-2:int(len(x0)/2)+2], y0[int(len(y0)/2)-2:int(len(y0)/2)+2], s = 50, c='red')
#cb = plt.colorbar(sc,fraction=0.045) # 调整colorbar的大小和图之间的间距
#cb.ax.tick_params(labelsize=20)
#plt.xlim(datalen - vallen,datalen + vallen)
plt.xlim(np.min(x0),np.max(x0))
plt.ylim(valmin, valmax)
yrange = 0.1
c1 = -yrange*np.ones(len(x0))
c2 = yrange*np.ones(len(x0))
plt.fill_between(x0, c1, c2, color = 'blue', alpha = 0.1)
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 30,
}
plt.yticks(fontproperties='Times New Roman', size = 25)
plt.ylabel("E", font2)
plt.xlabel("Energy Level", font2)
plt.xticks([])
plt.yticks([-1,0,1])
plt.savefig(picname, dpi = 100, bbox_inches = 'tight')
plt.close()
#---------------------------------------------------------
def charge(cont):
dataname = "ldos-" + str(cont).rjust(2,'0') + ".dat"
dataname = "dos.dat"
picname = "charge-" + str(cont).rjust(2,'0') + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = []
y0 = []
z0 = []
z1 = []
with open(dataname) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 3:
ldos = [float(x) for x in f1.strip().split()]
x0.append(ldos[0])
y0.append(ldos[1])
z0.append(ldos[2])
z1.append(ldos[3])
z0 = (z0 - np.min(z0))/(np.max(z0) - np.min(z0))*500 # 数据归一化
z2 = [abs(x-2)*5000 for x in z1] # 定义scatter的大小
z3 = [(x-2)*1000 for x in z1] # 定义scatter的颜色,因为这里电荷有正有负
plt.figure(figsize=(15, 15))
# sc = plt.scatter(x0, y0, c = z0,s = z0,vmin=0, vmax=1,cmap="seismic",edgecolor="black")
sc = plt.scatter(x0, y0, c = z3,s = z2,vmin=-0.5, vmax=0.5,cmap="inferno",edgecolor="black") # 残余电荷密度
cb = plt.colorbar(sc,fraction = 0.045) # 调整colorbar的大小和图之间的间距
cb.ax.tick_params(labelsize = 30)
cb.set_ticks(np.linspace(-0.5,0.5,2))
cb.set_ticklabels(('-0.5','0.5'))
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 40,
}
cb.set_label('Charge Density',fontdict=font2) #设置colorbar的标签字体及其大小
plt.scatter(x0, y0, s = 5, color='blue',edgecolor="blue")
plt.axis('scaled')
plt.xlabel("x",font2)
plt.ylabel("y",font2)
plt.title("Charge Distrubution",font2)
plt.yticks([0,15,30],fontproperties='Times New Roman', size = 30)
plt.xticks([0,15,30],fontproperties='Times New Roman', size = 30)
plt.savefig(picname, dpi = 100)
plt.close()
#---------------------------------------------------------
def main1():
for i0 in range(1,2):
ldosplt(i0)
eigval(i0)
charge(i0)
#---------------------------------------------------------
if __name__=="__main__":
main1()
 {:height=”50%” width=”50%”}
{:height=”50%” width=”50%”}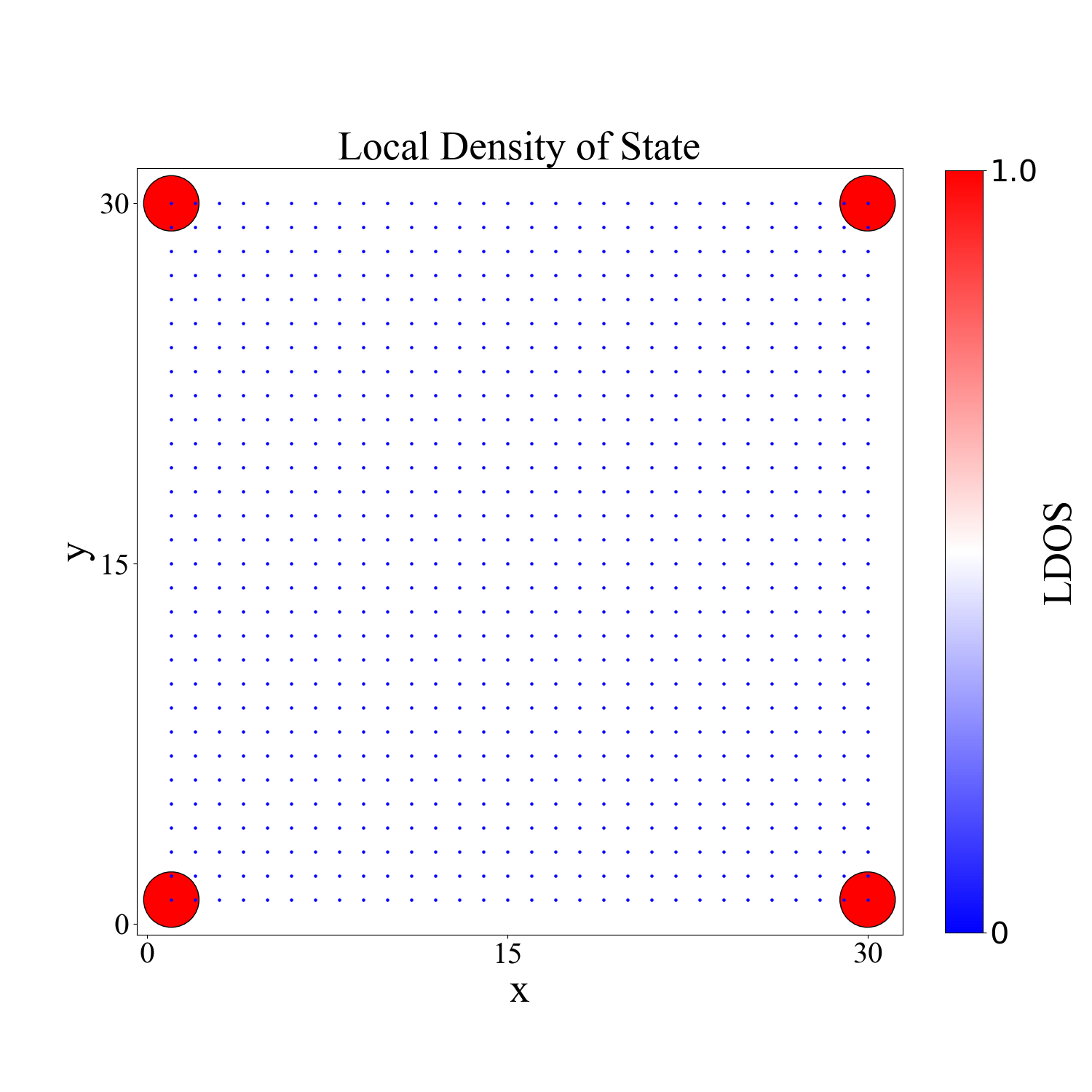 {:height=”50%” width=”50%”}
{:height=”50%” width=”50%”}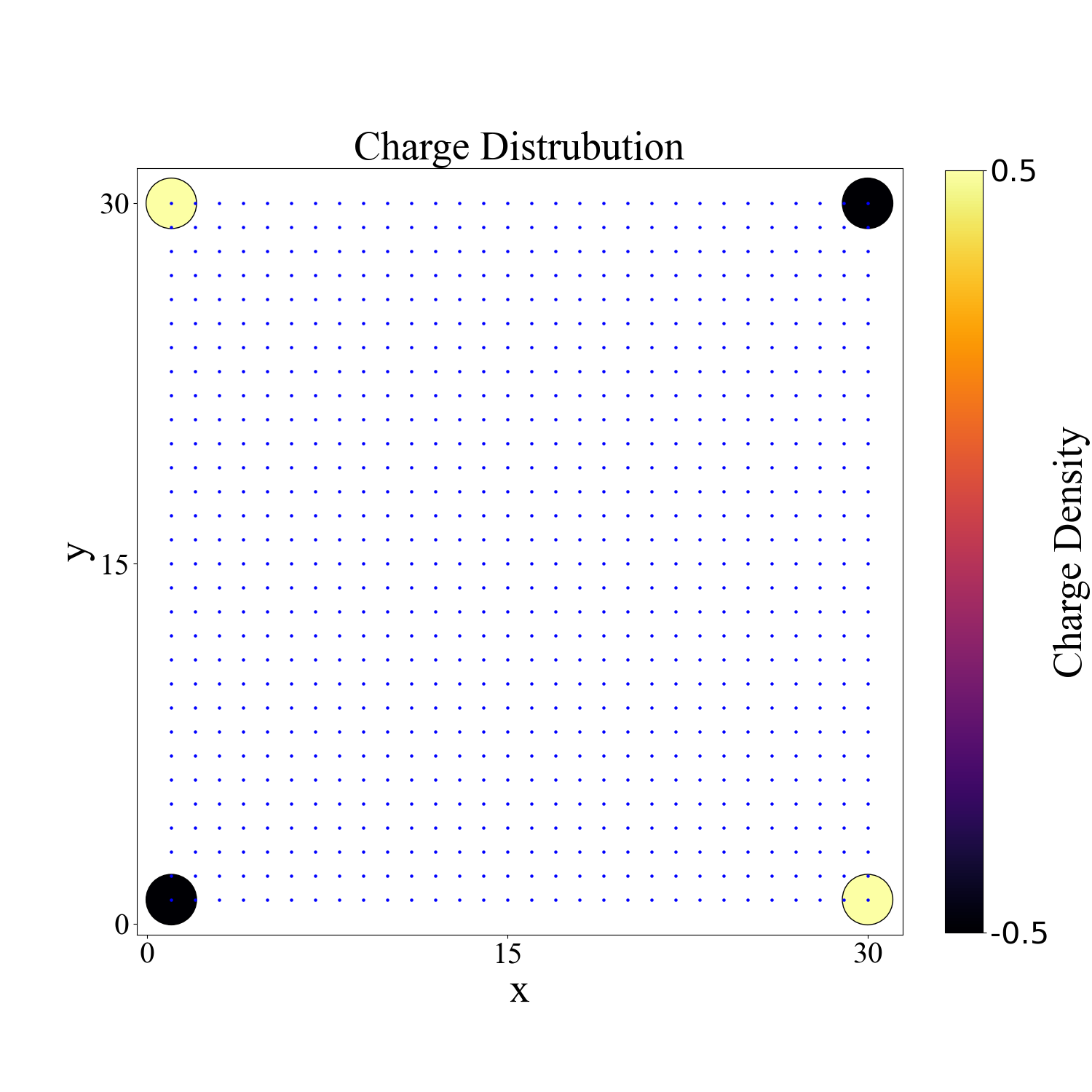 {:height=”50%” width=”50%”}
{:height=”50%” width=”50%”}
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |