这里在实空间中构建一个上三角形状来计算一些系统的性质。
{:.info}

前言

虽然自己经常研究的是正方点阵体系，但是有时候还是需要在一些特殊的形状上来计算系统的性质，这里就来构建一个上三角的格点模型来计算。

代码

废话不多说，直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
# 构建三角区域计算
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles,Printf
# --------------------------------------
@everywhere function boundary(xn::Int64,yn::Int64)
    # 构建在特定形状格点上的hopping位置
    len2::Int64 = xn*yn
    bry = zeros(Int64,4,len2)
    # f1 = open("tri.dat","w")
    for iy = 1:yn,ix in 1:iy  
        i = Int(iy*(iy - 1)/2) + ix
        bry[1,i] = i + 1    # right hopping
        if ix==iy 
            bry[1,i] = bry[1,i] - iy     
        end
        bry[2,i] = i - 1    # left hopping
        if ix==1
            bry[2,i] = bry[2,i] + iy      
        end
        bry[3,i] = i + iy   # up hopping
        if iy==yn 
            bry[3,i] = (ix + 1)*ix/2
        end
        bry[4,i]= i - (iy - 1)    # down hopping
        if iy==ix 
            bry[4,i] = yn*(yn - 1)/2 + ix
        end
        # writedlm(f1,[ix iy i bry[1,i] bry[2,i] bry[3,i] bry[4,i]])
    end
    # close(f1)
    return bry
end
#-------------------------------------
@everywhere function pauli()
    s0 = zeros(ComplexF64,2,2)
    s1 = zeros(ComplexF64,2,2)
    s2 = zeros(ComplexF64,2,2)
    s3 = zeros(ComplexF64,2,2)
    #----
    s0[1,1] = 1
    s0[2,2] = 1
    #----
    s1[1,2] = 1
    s1[2,1] = 1
    #----
    s2[1,2] = -im
    s2[2,1] = im
    #-----
    s3[1,1] = 1
    s3[2,2] = -1
    #-----
    return s0,s1,s2,s3
end
#---------------------------------------
@everywhere function gamma()
    s0,sx,sy,sz = pauli()
    g1 = kron(sz,s0,sz) # mass term
    g2 = kron(s0,sz,sx) # lambdax
    g3 = kron(sz,s0,sy) # lambday
    g4 = kron(sy,sy,s0) # dx^2-y^2
    g5 = kron(sx,sy,s0) # dxy
    g6 = kron(sz,sx,s0) # Zeeman
    g7 = kron(sz,s0,s0) # mu
    return g1,g2,g3,g4,g5,g6,g7
end
#-------------------------------------------------------------------------
@everywhere function matset(xn::Int64,yn::Int64)
    m0::Float64 = 1.0
    tx::Float64 = 2.0
    ty::Float64 = 2.0
    txy::Float64 = .0
    ax::Float64 = 2.0
    ay::Float64 = 2.0
    d0::Float64 = 0.
    dx::Float64 = 0.5
    dy::Float64 = -dx
    dp::Float64 = 0.
    mu::Float64 = 0.
    h0::Float64 = .0
    hn::Int64 = 8
    len2::Int64 = Int(xn*(yn + 1)/2)
    N::Int64 = len2*hn  #通过格点确定哈密顿量的大小
    ham = zeros(ComplexF64,N,N)
    g1,g2,g3,g4,g5,g6,g7 = gamma()
    bry = boundary(xn,yn)
    for iy in 1:yn,ix in 1:iy
        i0 = Int(iy*(iy - 1)/2) + ix
        for i1 in 0:hn -1,i2 in 0:hn - 1
            ham[i0 + len2*i1,i0 + len2*i2] = m0*g1[i1 + 1,i2 + 1] + d0*g4[i1 + 1,i2 + 1] - mu*g7[i1 + 1,i2 + 1] + h0*g6[i1 + 1,i2 + 1]
            if ix != iy
                ham[i0 + len2*i1,bry[1,i0] + len2*i2] = -tx/2.0*g1[i1 + 1,i2 + 1] + ax/(2*im)*g2[i1 + 1,i2 + 1] + dx/2.0*g4[i1 + 1,i2 + 1]
            end
            if ix != 1
                ham[i0 + len2*i1,bry[2,i0] + len2*i2] = -tx/2.0*g1[i1 + 1,i2 + 1] - ax/(2*im)*g2[i1 + 1,i2 + 1] + dx/2.0*g4[i1 + 1,i2 + 1]
            end
            if iy != yn
                ham[i0 + len2*i1,bry[3,i0] + len2*i2] = -ty/2.0*g1[i1 + 1,i2 + 1] + ay/(2*im)*g3[i1 + 1,i2 + 1] + dy/2.0*g4[i1 + 1,i2 + 1]
            end
            if iy != ix
                ham[i0 + len2*i1,bry[4,i0] + len2*i2] = -ty/2.0*g1[i1 + 1,i2 + 1] - ay/(2*im)*g3[i1 + 1,i2 + 1] + dy/2.0*g4[i1 + 1,i2 + 1]
            end
        end
    end
    if ishermitian(ham)
        val,vec = eigen(ham)
    else
        println("Hamiltonian is not hermitian")
        # break
    end
    temp = (a->(@sprintf "%3.2f" a)).(mu) # 将值转化成标准的字符串
    fx1 = "trival-" * temp * ".dat"
    f1 = open(fx1,"w")
    ind = (a->(@sprintf "%5.2f" a)).(range(1,length(val),length = length(val)))
    val2 = (a->(@sprintf "%15.8f" a)).(map(real,val))
    # writedlm(f1,map(real,val),"\t")
    writedlm(f1,[ind val2],"\t")
    close(f1)
    return map(real,val),vec
end
#----------------------------------------
@everywhere function delta(x::Float64)
    gamma::Float64 = 0.01
    return 1.0/pi*gamma/(x*x + gamma*gamma)
end
#------------------------------------------------------------------
@everywhere function ldos(h0::Float64)
# 计算实空间中零能态密度分布
    xn::Int64 = 30
    yn::Int64 = xn
    hn::Int64 = 8
    len2::Int64 = Int(xn*(yn + 1)/2)
    N::Int64 = len2*hn  #通过格点确定哈密顿量的大小
    omg::Float64 = 0.0
    val,vec = matset(xn,yn)
    fx1 = "trildos-" * string(h0) * ".dat"
    f1 = open(fx1,"w")
    for iy in 1:yn,ix in 1:iy
        i0 = Int(iy*(iy - 1)/2) + ix
        re1 = 0
        re2 = 0
        for ie in 1:N
            for i1 in 0:7
                re1 = re1 + delta(val[ie] - omg)*(abs(vec[i0 + len2*i1,ie])^2)
            end
        end
        for ie in 1:Int(N/2)
            for i1 in 0:7
                re2 += abs(vec[i0 + len2*i1,ie])^2
            end
        end
        @printf(f1,"%5.2f\t%5.2f\t%15.8f\t%15.8f\n",ix,iy,re1,re2)
        #writedlm(f1,[ix iy re1 re2],"\t")
    end
    close(f1)
end
#------------------------------------------------------------------
@everywhere function wave1(h0::Float64)
# 计算零能态波函数的分布
    xn::Int64 = 30
    yn::Int64 = xn
    hn::Int64 = 8
    len2::Int64 = Int(xn*(yn + 1)/2)
    N::Int64 = len2*hn  #通过格点确定哈密顿量的大小
    omg::Float64 = 0.0
    val,vec = matset(xn,yn)
    temp = (a->(@sprintf "%3.2f" a)).(h0)
    fx1 = "triwave-" * temp * ".dat"
    f1 = open(fx1,"w")
    for iy in 1:yn,ix in 1:iy
        i0 = Int(iy*(iy - 1)/2) + ix
        re1 = 0
        re2 = 0
        for m1 = 0:7
            for m2 = -1:2 # 遍历本征值
                re1 = re1 + abs(vec[i0 + m1*len2, Int(N/2) + m2])^2
            end 
        end 
        for ie in 1:Int(N/2) # 占据态波函数求和，得到每个格点上占据的电子数
            for i1 in 0:7
                re2 += abs(vec[i0 + len2*i1,ie])^2
            end
        end
        writedlm(f1,[ix iy re1 re2],"\t")
    end
    close(f1) 
end

#-------------------------------------------------------------------------
@time wave1(0.0)
@time ldos(0.0)

利用得到的数据进行绘图

绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------
def ldosplot2():
    dataname = "trildos-0.0.dat"
    picname = "tri.png"
    os.chdir(os.getcwd())# 确定用户执行路径
    dat = np.loadtxt(dataname)
    z0 = dat[:,2]
    z0 = (z0 - np.min(z0))/(np.max(z0) - np.min(z0))*1000 # 数据归一化
    plt.figure(figsize=(8, 8))
    #sc = plt.scatter(x0, y0, c = z0,s = z0,vmin=0, vmax=1,cmap="coolwarm",edgecolor="black") 
    sc = plt.scatter(dat[:,0], dat[:,1], c = z0,s = z0,vmin=0, vmax=1,cmap="bwr",edgecolor="black") 
    cb = plt.colorbar(sc,fraction = 0.045)  # 调整colorbar的大小和图之间的间距
    cb.ax.tick_params(labelsize=20)
    font2 = {'family': 'Times New Roman',
             'weight': 'normal',
             'size': 40,
             }
    # cb.set_label('ldos',fontdict=font2) #设置colorbar的标签字体及其大小
    plt.scatter(dat[:,0], dat[:,1], s = 5, color='blue',edgecolor="blue")
    plt.axis('scaled')
    # tit = "$\mu$ = " + cont
    # plt.title(tit,font2)
    plt.xlabel("x",font2)
    plt.ylabel("y",font2)
    #plt.title("|C| = 1",size = 20,fontproperties='Times New Roman')
    plt.yticks([1,15,30],fontproperties='Times New Roman', size = 30)
    plt.xticks([1,15,30],fontproperties='Times New Roman', size = 30)
    plt.savefig(picname, dpi=100,bbox_inches = 'tight')
    # plt.show()
    plt.close()
#-----------------------------------------------------
def eigval():
    # dataname = "val-" + cont + ".dat"
    # picname = "val-" + cont + ".png"
    dataname = "trival-0.00.dat"
    picname = "val.png"
    x0 = []
    y0 = []
    with open(dataname) as file:
        da = file.readlines()
        for f1 in da:
            if len(f1) > 2:
                da1 = [float(x) for x in f1.strip().split()]
                x0.append(da1[0])
                y0.append(da1[1])
    # plt.plot(x0, y0)
    # plt.title("|C| = 1",size = 20,fontproperties='Times New Roman')
    datalen = int(len(x0)/2)
    vallen = 30
    len1 = int(len(y0)/2)
    y0 = y0[len1 - vallen:len1 + vallen]
    valmin = np.min(y0)
    valmax = np.max(y0)
    x0 = range(len(y0))
    #----------------------------------
    plt.figure(figsize=(7, 6))
    sc = plt.scatter(x0, y0, s = 40,c='blue')
    # sc = plt.scatter(x0[int(len(x0)/2)-2:int(len(x0)/2)+2], y0[int(len(y0)/2)-2:int(len(y0)/2)+2], s = 50, c='red')
    #cb = plt.colorbar(sc,fraction=0.045)  # 调整colorbar的大小和图之间的间距
    #cb.ax.tick_params(labelsize=20)
    #plt.xlim(datalen - vallen,datalen + vallen)
    plt.xlim(np.min(x0),np.max(x0))
    plt.ylim(valmin, valmax)
    yrange = 0.1
    c1 = -yrange*np.ones(len(x0))
    c2 = yrange*np.ones(len(x0))
    plt.fill_between(x0, c1, c2, color = 'blue', alpha = 0.1)
    font2 = {'family': 'Times New Roman',
             'weight': 'normal',
             'size': 30,
             }
    # tit = "$\mu$ = " + cont
    # plt.title(tit,font2)
    plt.yticks(fontproperties='Times New Roman', size = 25)
    plt.ylabel("E", font2)
    plt.xlabel("Energy Level", font2)
    plt.xticks([])
    plt.yticks([-0.7,0,0.7])
    plt.savefig(picname, dpi=100, bbox_inches = 'tight')
    plt.close()
#-----------------------------------------------------
if __name__=="__main__":
    ldosplot2()
    eigval()

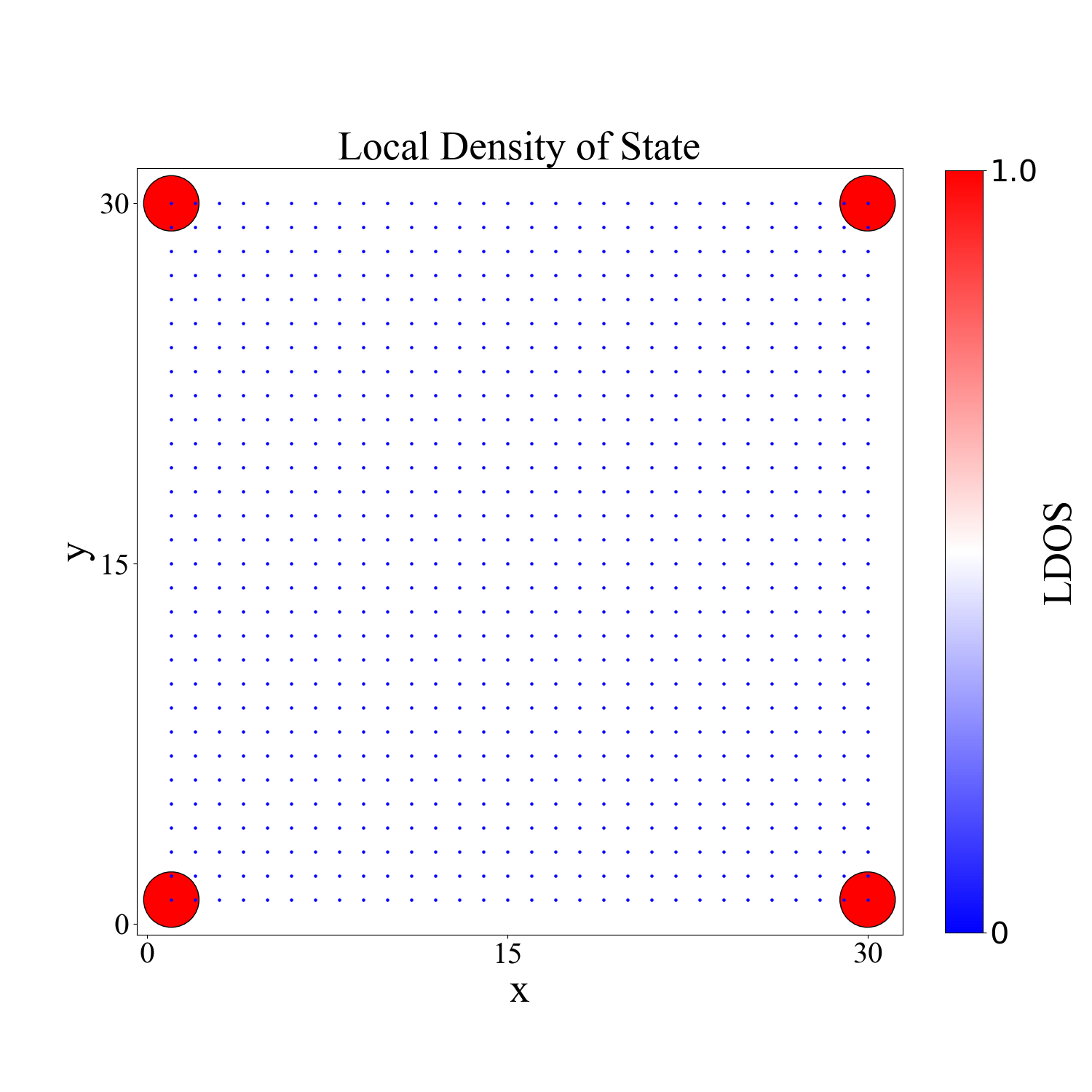
实空间中零能态密度分布为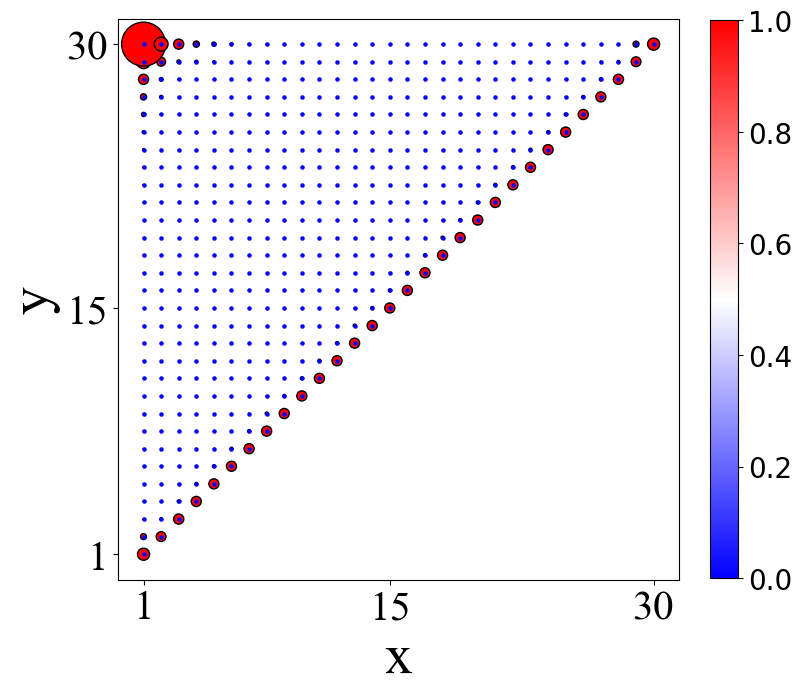
png

本征值为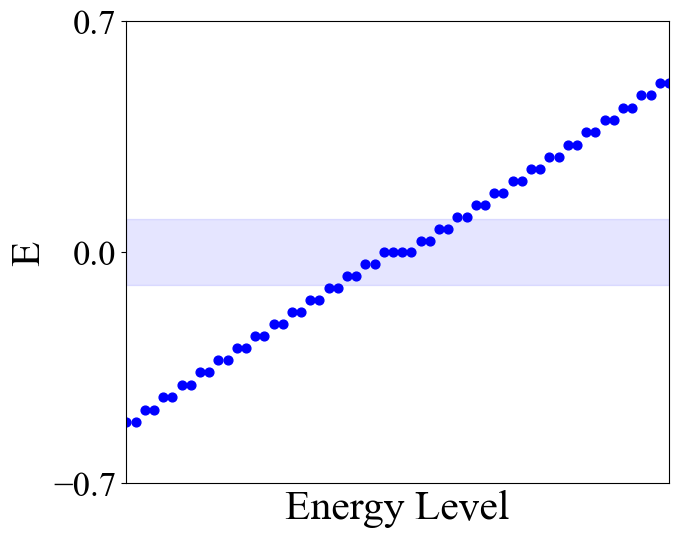
png

参考

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
{:.info}

QR Code

Email

yxliphy@gmail.com