这里在实空间中构建一个上三角形状来计算一些系统的性质。
前言
虽然自己经常研究的是正方点阵体系,但是有时候还是需要在一些特殊的形状上来计算系统的性质,这里就来构建一个上三角的格点模型来计算。
代码
废话不多说,直接上代码
# 构建三角区域计算
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles,Printf
# --------------------------------------
@everywhere function boundary(xn::Int64,yn::Int64)
# 构建在特定形状格点上的hopping位置
len2::Int64 = xn*yn
bry = zeros(Int64,4,len2)
# f1 = open("tri.dat","w")
for iy = 1:yn,ix in 1:iy
i = Int(iy*(iy - 1)/2) + ix
bry[1,i] = i + 1 # right hopping
if ix==iy
bry[1,i] = bry[1,i] - iy
end
bry[2,i] = i - 1 # left hopping
if ix==1
bry[2,i] = bry[2,i] + iy
end
bry[3,i] = i + iy # up hopping
if iy==yn
bry[3,i] = (ix + 1)*ix/2
end
bry[4,i]= i - (iy - 1) # down hopping
if iy==ix
bry[4,i] = yn*(yn - 1)/2 + ix
end
# writedlm(f1,[ix iy i bry[1,i] bry[2,i] bry[3,i] bry[4,i]])
end
# close(f1)
return bry
end
#-------------------------------------
@everywhere function pauli()
s0 = zeros(ComplexF64,2,2)
s1 = zeros(ComplexF64,2,2)
s2 = zeros(ComplexF64,2,2)
s3 = zeros(ComplexF64,2,2)
#----
s0[1,1] = 1
s0[2,2] = 1
#----
s1[1,2] = 1
s1[2,1] = 1
#----
s2[1,2] = -im
s2[2,1] = im
#-----
s3[1,1] = 1
s3[2,2] = -1
#-----
return s0,s1,s2,s3
end
#---------------------------------------
@everywhere function gamma()
s0,sx,sy,sz = pauli()
g1 = kron(sz,s0,sz) # mass term
g2 = kron(s0,sz,sx) # lambdax
g3 = kron(sz,s0,sy) # lambday
g4 = kron(sy,sy,s0) # dx^2-y^2
g5 = kron(sx,sy,s0) # dxy
g6 = kron(sz,sx,s0) # Zeeman
g7 = kron(sz,s0,s0) # mu
return g1,g2,g3,g4,g5,g6,g7
end
#-------------------------------------------------------------------------
@everywhere function matset(xn::Int64,yn::Int64)
m0::Float64 = 1.0
tx::Float64 = 2.0
ty::Float64 = 2.0
txy::Float64 = .0
ax::Float64 = 2.0
ay::Float64 = 2.0
d0::Float64 = 0.
dx::Float64 = 0.5
dy::Float64 = -dx
dp::Float64 = 0.
mu::Float64 = 0.
h0::Float64 = .0
hn::Int64 = 8
len2::Int64 = Int(xn*(yn + 1)/2)
N::Int64 = len2*hn #通过格点确定哈密顿量的大小
ham = zeros(ComplexF64,N,N)
g1,g2,g3,g4,g5,g6,g7 = gamma()
bry = boundary(xn,yn)
for iy in 1:yn,ix in 1:iy
i0 = Int(iy*(iy - 1)/2) + ix
for i1 in 0:hn -1,i2 in 0:hn - 1
ham[i0 + len2*i1,i0 + len2*i2] = m0*g1[i1 + 1,i2 + 1] + d0*g4[i1 + 1,i2 + 1] - mu*g7[i1 + 1,i2 + 1] + h0*g6[i1 + 1,i2 + 1]
if ix != iy
ham[i0 + len2*i1,bry[1,i0] + len2*i2] = -tx/2.0*g1[i1 + 1,i2 + 1] + ax/(2*im)*g2[i1 + 1,i2 + 1] + dx/2.0*g4[i1 + 1,i2 + 1]
end
if ix != 1
ham[i0 + len2*i1,bry[2,i0] + len2*i2] = -tx/2.0*g1[i1 + 1,i2 + 1] - ax/(2*im)*g2[i1 + 1,i2 + 1] + dx/2.0*g4[i1 + 1,i2 + 1]
end
if iy != yn
ham[i0 + len2*i1,bry[3,i0] + len2*i2] = -ty/2.0*g1[i1 + 1,i2 + 1] + ay/(2*im)*g3[i1 + 1,i2 + 1] + dy/2.0*g4[i1 + 1,i2 + 1]
end
if iy != ix
ham[i0 + len2*i1,bry[4,i0] + len2*i2] = -ty/2.0*g1[i1 + 1,i2 + 1] - ay/(2*im)*g3[i1 + 1,i2 + 1] + dy/2.0*g4[i1 + 1,i2 + 1]
end
end
end
if ishermitian(ham)
val,vec = eigen(ham)
else
println("Hamiltonian is not hermitian")
# break
end
temp = (a->(@sprintf "%3.2f" a)).(mu) # 将值转化成标准的字符串
fx1 = "trival-" * temp * ".dat"
f1 = open(fx1,"w")
ind = (a->(@sprintf "%5.2f" a)).(range(1,length(val),length = length(val)))
val2 = (a->(@sprintf "%15.8f" a)).(map(real,val))
# writedlm(f1,map(real,val),"\t")
writedlm(f1,[ind val2],"\t")
close(f1)
return map(real,val),vec
end
#----------------------------------------
@everywhere function delta(x::Float64)
gamma::Float64 = 0.01
return 1.0/pi*gamma/(x*x + gamma*gamma)
end
#------------------------------------------------------------------
@everywhere function ldos(h0::Float64)
# 计算实空间中零能态密度分布
xn::Int64 = 30
yn::Int64 = xn
hn::Int64 = 8
len2::Int64 = Int(xn*(yn + 1)/2)
N::Int64 = len2*hn #通过格点确定哈密顿量的大小
omg::Float64 = 0.0
val,vec = matset(xn,yn)
fx1 = "trildos-" * string(h0) * ".dat"
f1 = open(fx1,"w")
for iy in 1:yn,ix in 1:iy
i0 = Int(iy*(iy - 1)/2) + ix
re1 = 0
re2 = 0
for ie in 1:N
for i1 in 0:7
re1 = re1 + delta(val[ie] - omg)*(abs(vec[i0 + len2*i1,ie])^2)
end
end
for ie in 1:Int(N/2)
for i1 in 0:7
re2 += abs(vec[i0 + len2*i1,ie])^2
end
end
@printf(f1,"%5.2f\t%5.2f\t%15.8f\t%15.8f\n",ix,iy,re1,re2)
#writedlm(f1,[ix iy re1 re2],"\t")
end
close(f1)
end
#------------------------------------------------------------------
@everywhere function wave1(h0::Float64)
# 计算零能态波函数的分布
xn::Int64 = 30
yn::Int64 = xn
hn::Int64 = 8
len2::Int64 = Int(xn*(yn + 1)/2)
N::Int64 = len2*hn #通过格点确定哈密顿量的大小
omg::Float64 = 0.0
val,vec = matset(xn,yn)
temp = (a->(@sprintf "%3.2f" a)).(h0)
fx1 = "triwave-" * temp * ".dat"
f1 = open(fx1,"w")
for iy in 1:yn,ix in 1:iy
i0 = Int(iy*(iy - 1)/2) + ix
re1 = 0
re2 = 0
for m1 = 0:7
for m2 = -1:2 # 遍历本征值
re1 = re1 + abs(vec[i0 + m1*len2, Int(N/2) + m2])^2
end
end
for ie in 1:Int(N/2) # 占据态波函数求和,得到每个格点上占据的电子数
for i1 in 0:7
re2 += abs(vec[i0 + len2*i1,ie])^2
end
end
writedlm(f1,[ix iy re1 re2],"\t")
end
close(f1)
end
#-------------------------------------------------------------------------
@time wave1(0.0)
@time ldos(0.0)
利用得到的数据进行绘图
绘图
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------
def ldosplot2():
dataname = "trildos-0.0.dat"
picname = "tri.png"
os.chdir(os.getcwd())# 确定用户执行路径
dat = np.loadtxt(dataname)
z0 = dat[:,2]
z0 = (z0 - np.min(z0))/(np.max(z0) - np.min(z0))*1000 # 数据归一化
plt.figure(figsize=(8, 8))
#sc = plt.scatter(x0, y0, c = z0,s = z0,vmin=0, vmax=1,cmap="coolwarm",edgecolor="black")
sc = plt.scatter(dat[:,0], dat[:,1], c = z0,s = z0,vmin=0, vmax=1,cmap="bwr",edgecolor="black")
cb = plt.colorbar(sc,fraction = 0.045) # 调整colorbar的大小和图之间的间距
cb.ax.tick_params(labelsize=20)
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 40,
}
# cb.set_label('ldos',fontdict=font2) #设置colorbar的标签字体及其大小
plt.scatter(dat[:,0], dat[:,1], s = 5, color='blue',edgecolor="blue")
plt.axis('scaled')
# tit = "$\mu$ = " + cont
# plt.title(tit,font2)
plt.xlabel("x",font2)
plt.ylabel("y",font2)
#plt.title("|C| = 1",size = 20,fontproperties='Times New Roman')
plt.yticks([1,15,30],fontproperties='Times New Roman', size = 30)
plt.xticks([1,15,30],fontproperties='Times New Roman', size = 30)
plt.savefig(picname, dpi=100,bbox_inches = 'tight')
# plt.show()
plt.close()
#-----------------------------------------------------
def eigval():
# dataname = "val-" + cont + ".dat"
# picname = "val-" + cont + ".png"
dataname = "trival-0.00.dat"
picname = "val.png"
x0 = []
y0 = []
with open(dataname) as file:
da = file.readlines()
for f1 in da:
if len(f1) > 2:
da1 = [float(x) for x in f1.strip().split()]
x0.append(da1[0])
y0.append(da1[1])
# plt.plot(x0, y0)
# plt.title("|C| = 1",size = 20,fontproperties='Times New Roman')
datalen = int(len(x0)/2)
vallen = 30
len1 = int(len(y0)/2)
y0 = y0[len1 - vallen:len1 + vallen]
valmin = np.min(y0)
valmax = np.max(y0)
x0 = range(len(y0))
#----------------------------------
plt.figure(figsize=(7, 6))
sc = plt.scatter(x0, y0, s = 40,c='blue')
# sc = plt.scatter(x0[int(len(x0)/2)-2:int(len(x0)/2)+2], y0[int(len(y0)/2)-2:int(len(y0)/2)+2], s = 50, c='red')
#cb = plt.colorbar(sc,fraction=0.045) # 调整colorbar的大小和图之间的间距
#cb.ax.tick_params(labelsize=20)
#plt.xlim(datalen - vallen,datalen + vallen)
plt.xlim(np.min(x0),np.max(x0))
plt.ylim(valmin, valmax)
yrange = 0.1
c1 = -yrange*np.ones(len(x0))
c2 = yrange*np.ones(len(x0))
plt.fill_between(x0, c1, c2, color = 'blue', alpha = 0.1)
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 30,
}
# tit = "$\mu$ = " + cont
# plt.title(tit,font2)
plt.yticks(fontproperties='Times New Roman', size = 25)
plt.ylabel("E", font2)
plt.xlabel("Energy Level", font2)
plt.xticks([])
plt.yticks([-0.7,0,0.7])
plt.savefig(picname, dpi=100, bbox_inches = 'tight')
plt.close()
#-----------------------------------------------------
if __name__=="__main__":
ldosplot2()
eigval()
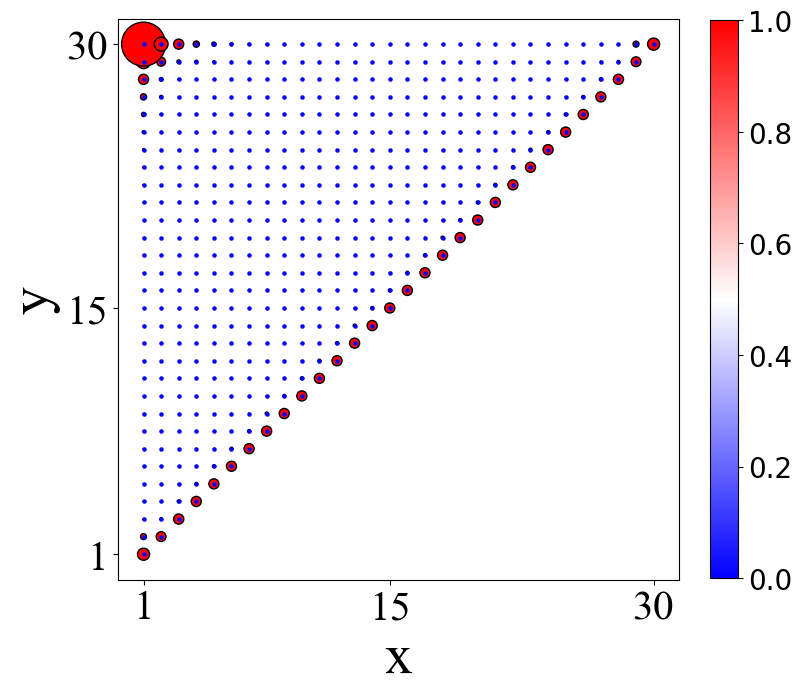
实空间中零能态密度分布为
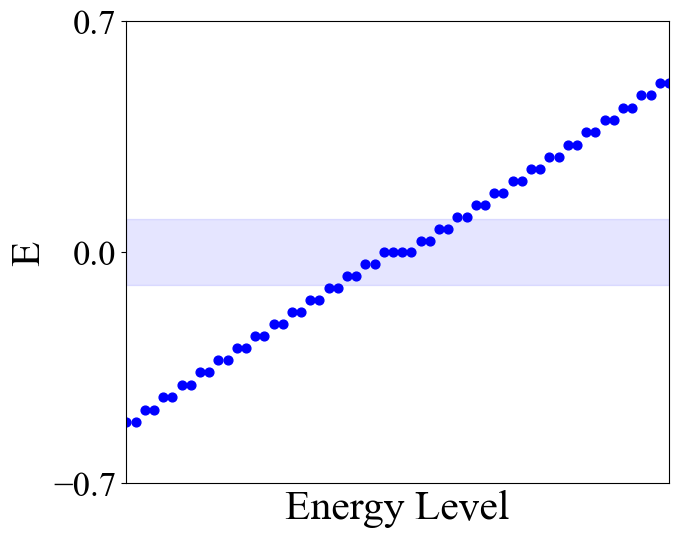
本征值为
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |