最近重新学习关于拓扑超导的知识,先整理一下学Kitaev $p$-wave 模型的计算代码。

模型介绍
Kitaev链是最简单的1D spinless $p$-wave 超导模型,和正常态的SSH模型会非常类似,其实空间的表示为
\[H=-\mu \sum_{x} c_{x}^{\dagger} c_{x}-\frac{1}{2} \sum_{x}\left(t c_{x}^{\dagger} c_{x+1}+\Delta \mathrm{e}^{\mathrm{i} \phi} c_{x} c_{x+1}+\text { H.c. }\right)\]这里引入Majorana 算符,其实形式上看起来就是将一个费米子算符拆开成一对Majorana算符
\[c_{x}=\frac{\mathrm{e}^{-\mathrm{i} \phi / 2}}{2}\left(\gamma_{B, x}+\mathrm{i} \gamma_{A, x}\right)\]新的Majorana费米子满足的仍然是反对易关系
\[\gamma_{\alpha, x}=\gamma_{\alpha, x}^{\dagger}, \quad\left\{\gamma_{\alpha, x}, \gamma_{\alpha^{\prime}, x^{\prime}}\right\}=2 \delta_{\alpha \alpha^{\prime}} \delta_{x x^{\prime}}\]在Majorana算符表示下,哈密顿量为
\[H=-\frac{\mu}{2} \sum_{x=1}^{N}\left(1+\mathrm{i} \gamma_{B, x} \gamma_{A, x}\right)-\frac{\mathrm{i}}{4} \sum^{N-1}\left[(\Delta+t) \gamma_{B, x} \gamma_{A, x+1}+(\Delta-t) \gamma_{A, x} \gamma_{B, x+1}\right]\label{q1}\end{aligned}\]这个时候就可以像分析SSH模型一样来分析Kitaev chain。首先取$\mu<0,t=\Delta=0$,此时系统处于平庸项,将这个参数代入哈密顿量\eqref{q1}中发现,原胞中的两个Majorana算符是相互绑定的,如上图所示
对于$\mu=0,t=\Delta\neq0$的参数,此时系统处于拓扑相,哈密顿量\eqref{q1}约化为
\[H=-\mathrm{i} \frac{t}{2} \sum_{x=1}^{N-1} \gamma_{B, x} \gamma_{A, x+1},\]可以发现相临原胞之间的Majorana算符配对,最后是的首尾的Majorana算符是孤立的,从而就形成了非局域的Majorana零能态,如下图所示

能带
在动量空间中,Kitaev $p$-wave模型为
\[H(\mathbf{k})=(2t\cos k-\mu)\tau_z + 2\Delta_0\sin k\tau_y\]就先不具体解释了,直接上代码计算
# 变化Zeeman场看实空间能谱演化
# 求解少量本征值
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles,Printf,Arpack
#-------------------------------------
@everywhere function pauli()
s0 = zeros(ComplexF64,2,2)
s1 = zeros(ComplexF64,2,2)
s2 = zeros(ComplexF64,2,2)
s3 = zeros(ComplexF64,2,2)
#----
s0[1,1] = 1
s0[2,2] = 1
#----
s1[1,2] = 1
s1[2,1] = 1
#----
s2[1,2] = -im
s2[2,1] = im
#-----
s3[1,1] = 1
s3[2,2] = -1
#-----
return s0,s1,s2,s3
end
#---------------------------------------------------------------
@everywhere function boundary(xn::Int64)
bry = zeros(Int64,2,xn)
for i0 in 1:xn
bry[1,i0] = i0 + 1
if i0 == xn
bry[1,i0] = bry[1,i0] - xn
end
bry[2,i0] = i0 - 1
if i0 == 1
bry[2,i0] = bry[2,i0] + xn
end
end
return bry
end
#-------------------------------------------------
@everywhere function matset(k::Float64)
t0::Float64 = 1.0
mu::Float64 = 1.0
d0::Float64 = 1.0
s0,sx,sy,sz = pauli()
ham = (-2*t0*cos(k) - mu)*sz + 2*d0*sin(k)*sy
return eigvals(ham)
end
#--------------------------------------------------------------
function band()
hn::Int64 = 2
kn::Int64 = 100
ham = zeros(ComplexF64,hn,hn)
vals1 = zeros(Float64,2*kn + 1,hn)
klist = []
for i1 in -kn:kn
kx = i1*pi/kn
append!(klist,kx/pi)
val1 = matset(kx)
vals1[i1 + kn + 1,:] = val1[:]
end
temp = (a->(@sprintf "%3.2f" a)).(1)
fn1 = "band-" * temp * ".dat"
f1 = open(fn1,"w")
klist = (a->(@sprintf "%15.8f" a)).(klist)
vals1 = (a->(@sprintf "%15.8f" a)).(vals1)
writedlm(f1,[klist vals1])
close(f1)
end
#-----------------------------------------------------------------------
@everywhere function realspace()
t0::Float64 = 1.0
mu::Float64 = 1.0
d0::Float64 = 1.0
hn::Int64 = 2
xn::Int64 = 50
N::Int64 = xn*hn
ham = zeros(ComplexF64,N,N)
s0,sx,sy,sz = pauli()
bry = boundary(xn)
for i0 in 1:xn
for i1 in 0:hn - 1,i2 in 0:hn - 1
ham[i0 + i1*xn,i0 + i2*xn] = -mu*sz[i1 + 1,i2 + 1]
if i0 != xn
ham[i0 + i1*xn,bry[1,i0] + i2*xn] = -t0*sz[i1 + 1,i2 + 1] + d0/(2*im)*sy[i1 + 1,i2 + 1]
end
if i0 != 1
ham[i0 + i1*xn,bry[2,i0] + i2*xn] = -t0*sz[i1 + 1,i2 + 1] - d0/(2*im)*sy[i1 + 1,i2 + 1]
end
end
end
vals = eigvals(ham)
fx1 = "real-vals.dat"
# fx1 = "eigval.dat"
f1 = open(fx1,"w")
ind = (a->(@sprintf "%5.2f" a)).(range(1,length(vals),length = length(vals)))
val2 = (a->(@sprintf "%15.8f" a)).(sort(map(real,vals)))
writedlm(f1,[ind val2],"\t")
close(f1)
end
#-------------------------------------------------------------------------------------------------
@time band()
@time realspace()
因为用Julia写并行习惯了,这里还是用了并行,执行时候需要加一些参数
julia -p 1 code.jl
绘图程序为
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 50,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------
def pltband():
# da1 = "m2-pro-ox-" + str(cont) + ".dat"
da1 = "band-1.00.dat"
picname = os.path.splitext(da1)[0] + ".png"
# picname = "ch" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
da = np.loadtxt(da1)
x0 = da[:,0]
y0 = da[:,1:]
plt.figure(figsize = (10,10))
plt.plot(x0,y0,lw = 3,c = 'b')
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 50,
}
y0min = np.min(y0)
y0max = np.max(y0)
tit = "Kitaev Chain"
plt.title(tit,font2)
plt.xlim(-1,1)
plt.ylim(y0min,y0max)
plt.xlabel(r'$k$',font2)
plt.ylabel(r'$E(k)$',font2)
plt.xticks([-1,0,1],fontproperties='Times New Roman', size = 50)
plt.yticks([y0min,0,y0max],fontproperties='Times New Roman', size = 50)
plt.savefig(picname, dpi = 100, bbox_inches = 'tight')
plt.close()
# plt.show()
#---------------------------------------------------------
def pltrealvals():
# da1 = "m2-pro-ox-" + str(cont) + ".dat"
da1 = "real-vals.dat"
picname = os.path.splitext(da1)[0] + ".png"
# picname = "ch" + str(cont) + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
da = np.loadtxt(da1)
x0 = da[:,0]
y0 = da[:,1:]
plt.figure(figsize = (10,10))
plt.scatter(x0,y0,s = 50,c = 'blue',edgecolor="black",label="Gap")
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 50,
}
plt.ylabel("E",font2)
plt.xlabel("State",font2)
plt.yticks([-2,0,2],fontproperties='Times New Roman', size = 50)
plt.xticks([],fontproperties='Times New Roman', size = 50)
y0min = np.min(y0)
y0max = np.max(y0)
x0min = np.min(x0)
x0max = np.max(x0)
plt.ylim(y0min,y0max)
plt.xlim(x0min,x0max)
plt.savefig(picname, dpi = 100, bbox_inches = 'tight')
# plt.show()
plt.close()
#---------------------------------------------------------
# def main():
# for i0 in range(1,2):
# # pltband(i0)
#---------------------------------------------------------
if __name__=="__main__":
# main()
pltrealvals()
pltband()
其动量空间和实空间的结果分别为
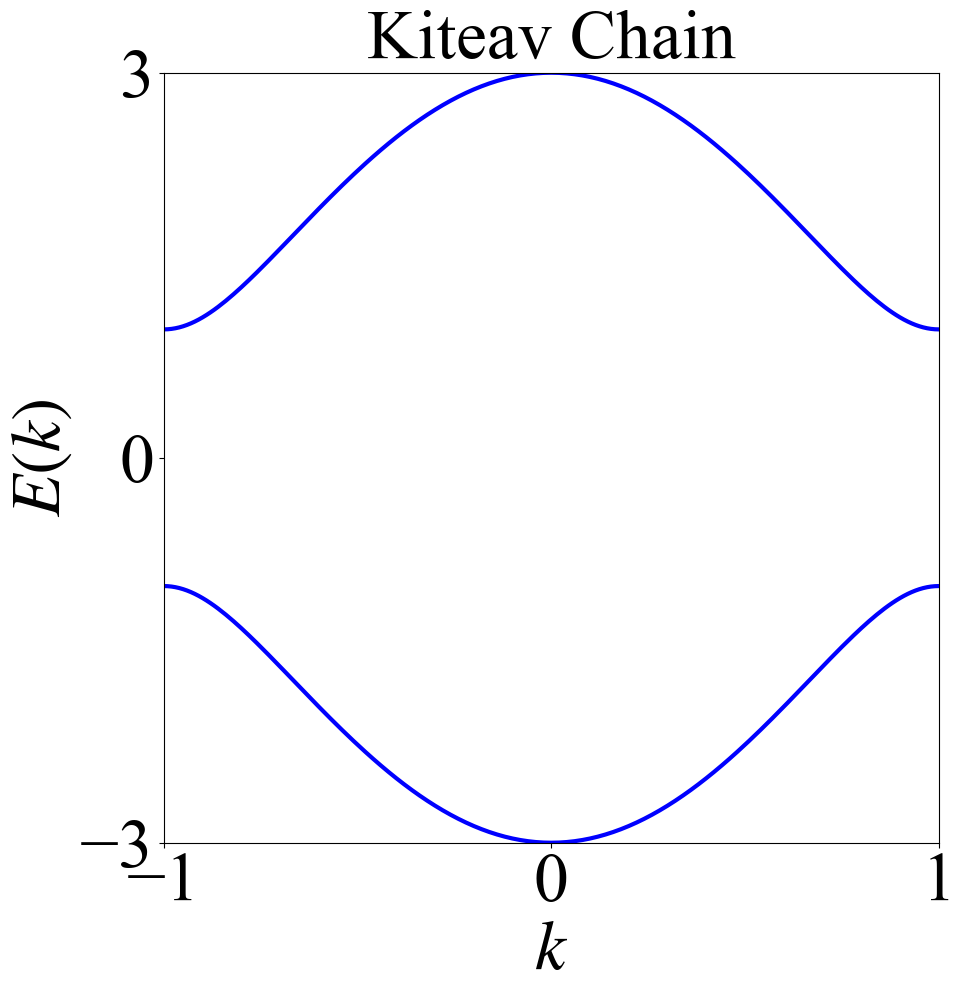
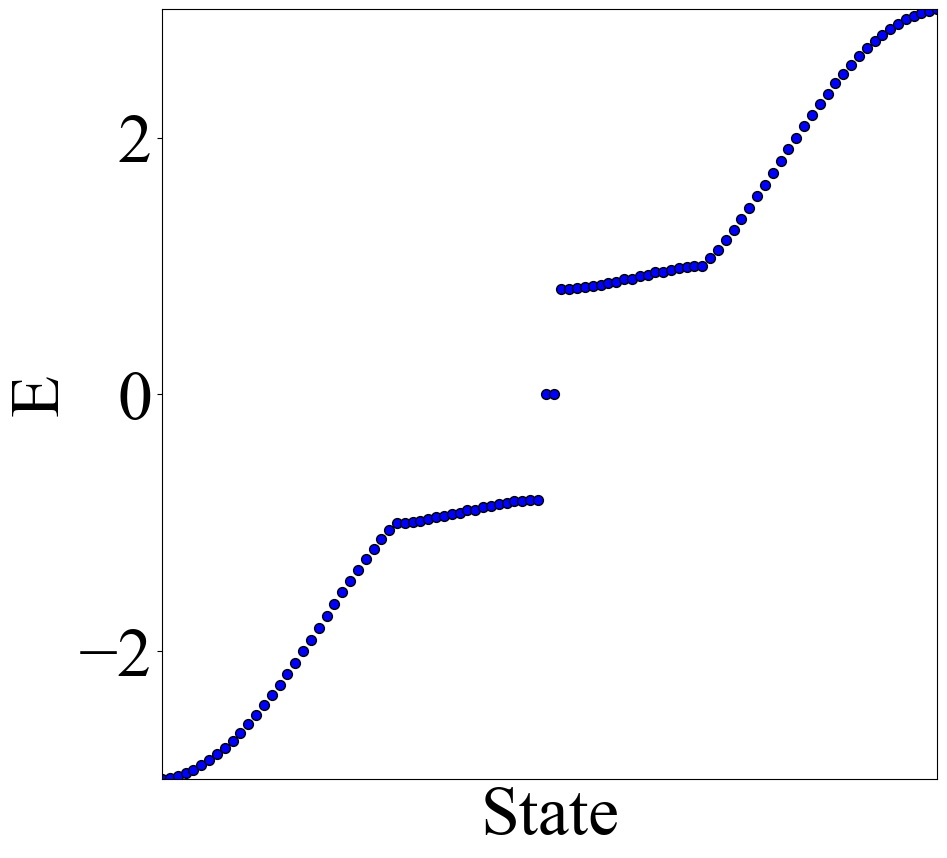
参考
- 1.New directions in the pursuit of Majorana fermions in solid state systems
- 2.Topological superconductors: a review
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |