最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。
Zero-dimensional quantum systems
假设一个量子系统具有$N$个量子态,那么这个系统的哈密顿量$H$就可以表示为一个$N\times N$的矩阵,同时这个矩阵要满足厄米$H^\dagger=H$,其对应的本征值是实数,满足的本征方程为
\[H\rvert n\rangle = E_n\rvert n\rangle\]这里的$\rvert n\rangle$就是系统的本征态。现在考虑$H$描述的是一个很小的量子点,它只有少数的几个能级,我们可以考虑它与一个金属导体存在弱耦合,如下图所示
当存在金属电极之后就可以测量量子点中的能级$E_n$,此时能量参考点是金属电极的费米能$E_f$,因此量子点中所有$E_n<0$的态为占据态,而$E_n>0$的则表示空态,如上图所示,在金属电极和量子点之间存在着势垒,所以电极和量子点之间的耦合很弱,此时仍然可以将量子点看作是一个孤立的系统,这是一个不错的近似。
Topology and gapped quantum systems
拓扑研究的是物体在连续变化的性质。在凝聚态物理中,如果两个量子系统可以连续的相互演化,那么就称它们是拓扑等价的,否则就是拓扑不等价。如果此时考虑的哈密顿量不存在任何的限制,每一个哈密顿量都可以连续的演化,那么所有的量子系统都是拓扑等价的。此时如果我们只考虑具有能隙的系统(比如绝缘体),此时系统的占据态和空态之间存在激发能隙,此时哈密顿量在能量为零处就不会存在本征值,此时就可以对物理中的拓扑给出判据: 如果两个系统的哈密顿量可以在不关闭能隙的前提下相互演化,那么就称这两个系统是拓扑等价的。In the following, we will see that often one is interested in some more specific criterion: for instance, that some symmetry may be preserved throughout the continuous path which connects two Hamiltonians.
下面先考虑最简单的量子点情形,假设最终系统的哈密顿量为$H$,他一定是一个厄米矩阵。现在考虑将哈密顿量演化成另外一个$H’$,这个演化过程可以看作是在量子点系统中通过调节电压实现的,可以将这个参数化过程表述为
\[H(\alpha) = \alpha H' + (1-\alpha) H,\]当$\alpha=0$时描述的是最初的哈密顿量,$\alpha=1$则是最终的哈密顿量,可以通过参数$\alpha$的变化来模拟这个过程
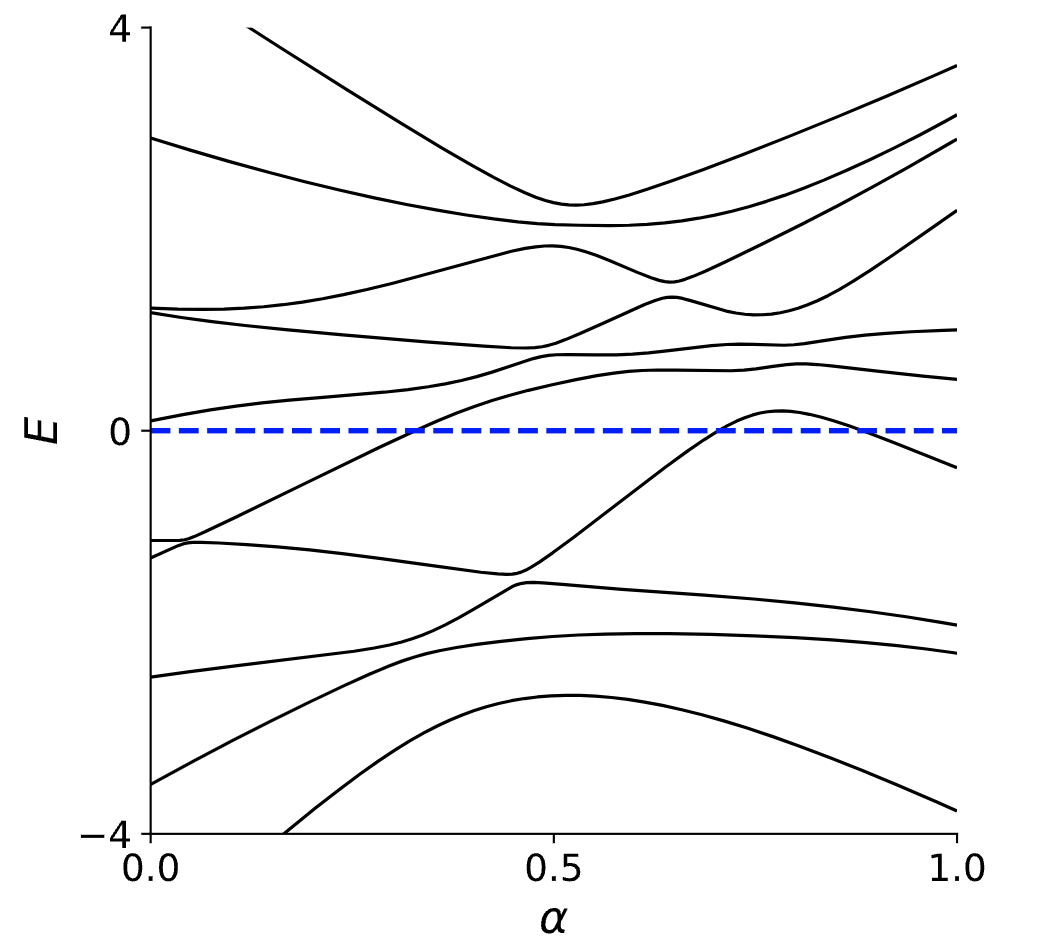
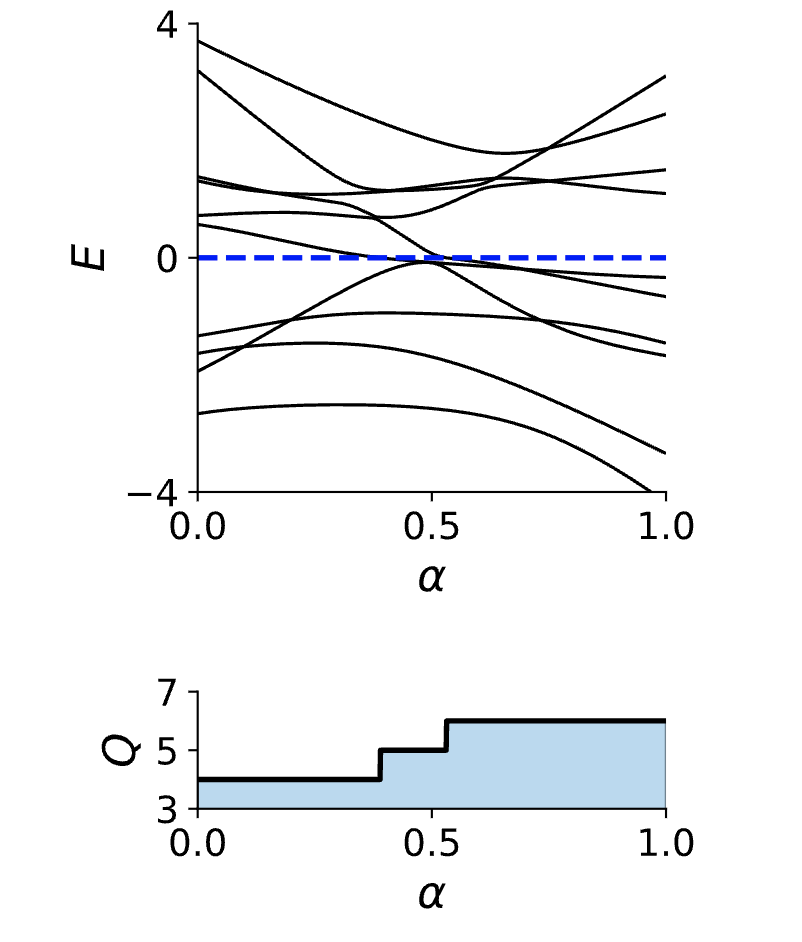
通过上图可以发现,随着参数$\alpha$的演化,一些能级会与$E=0$发生交叉,这就表明这个演化过程违背了上面定义的要存在能隙的要求。但是这并不意味着$H$和$H’$之间不存在连续且不关闭能隙的演化路径。即这里存在一条特殊的路径,可以令$H$到$H’$的演化路径是不经历能隙闭合的。比如下面的情况
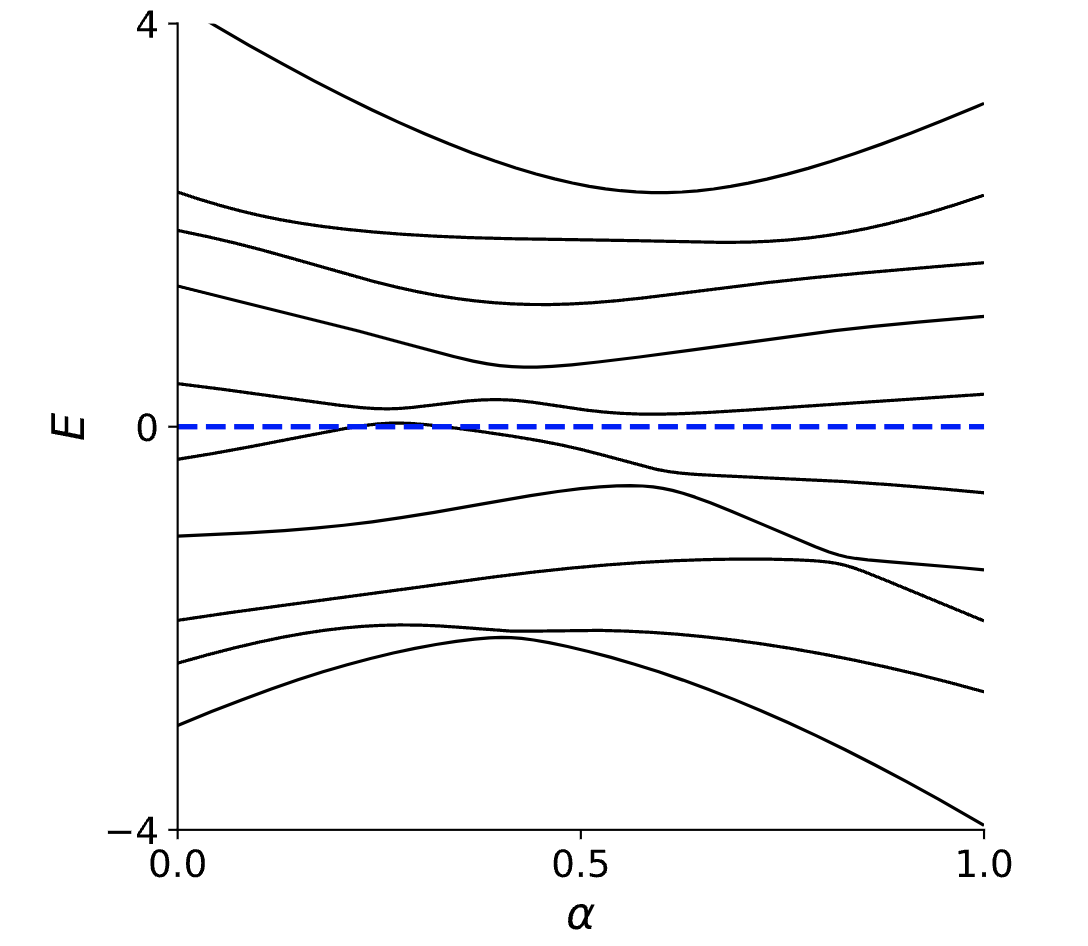
可以看到一个能级在演化过程中和$E=0$相交了两次,可以通过将能级稍微下移一点,从而就可以找到一条连续演化的路径。
The concept of a topological invariant
为了知道在$H\rightarrow H’$的过程中是否发生了能隙闭合,可以先统计能量等于零下面的能级数量,也就是占据态能级的数量。当参数$\alpha$进行演化的时候,只要能级不与$E=0$相交,这个方法就是可行的,所以如果是一个连续的演化过程,那么占据态的数量就始终是保持不变的。因为这个数对于一个有能隙的系统而言,在连续演化的过程中始终是不变的,所以就叫它为拓扑不变量Q。
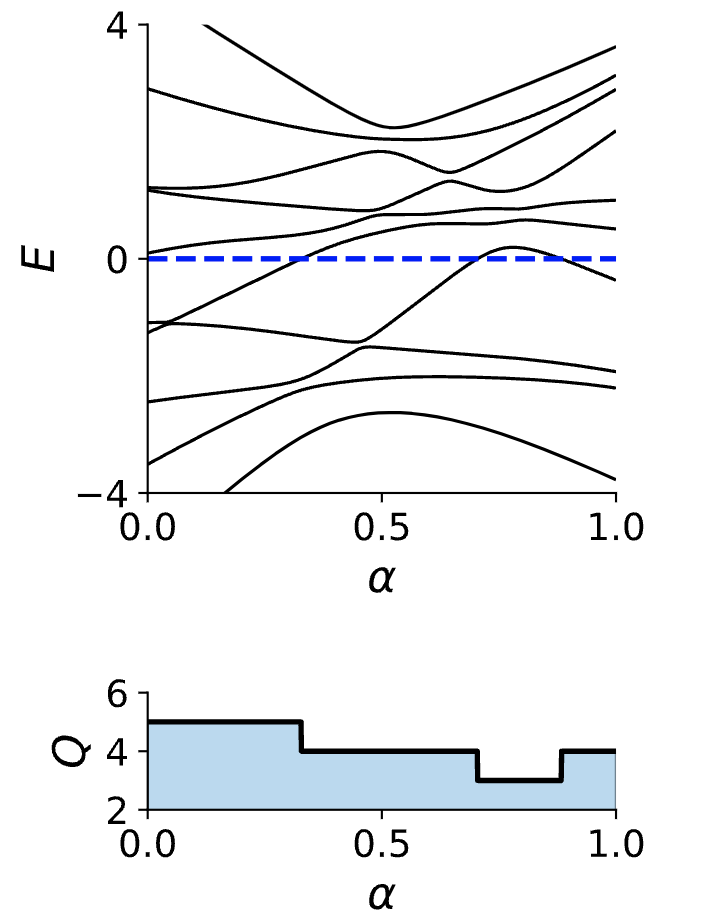
如上图所示,在参数$\alpha$变化过程中,$E=0$与能级相交的次数会发生变化,对应的拓扑不变量$Q$也发生了变化,所以可以说$H$和$H’$是不等价的。而每一次拓扑数的变化就称为拓扑相变。
如果两个哈密顿量具有不同的拓扑不变量,那么它们之间的一定会通过拓扑相变分离开,也就是说从$H\rightarrow H’$过程中会经历能隙的闭合与打开。相反,如果在参数演化过程当中,能级从下向上和从上向下与$E=0$相交的次数是相同的,那么相交次数就肯定是偶数次,此时一定可以找到一条连续的演化路径使得在$H\rightarrow H’$过程中不存在能隙闭合。
一旦我们可以确定体系的拓扑不变量$Q$,那么就可以利用这个量来对系统进行分类,具有相同拓扑不变量的系统是等价的,具有不同拓扑不变量的系统在演化过程中会经历能隙的闭合与打开,即发生拓扑相变。
Role of conservation laws
接下来考虑对称性对哈密顿量的限制。通常会存在一个幺正矩阵,比如$U = \sigma_z \otimes 1!!1$与哈密顿量满足对易关系
\[U^\dagger H U = H.\]意味着系统存在一个守恒量,在当前的对称操作下面,哈密顿量会是块对角化的形式

此时同样可以改变参数来研究体系的演化,只不过现在可以分别对每一个子块哈密顿量计算其能谱随着$\alpha$的变化
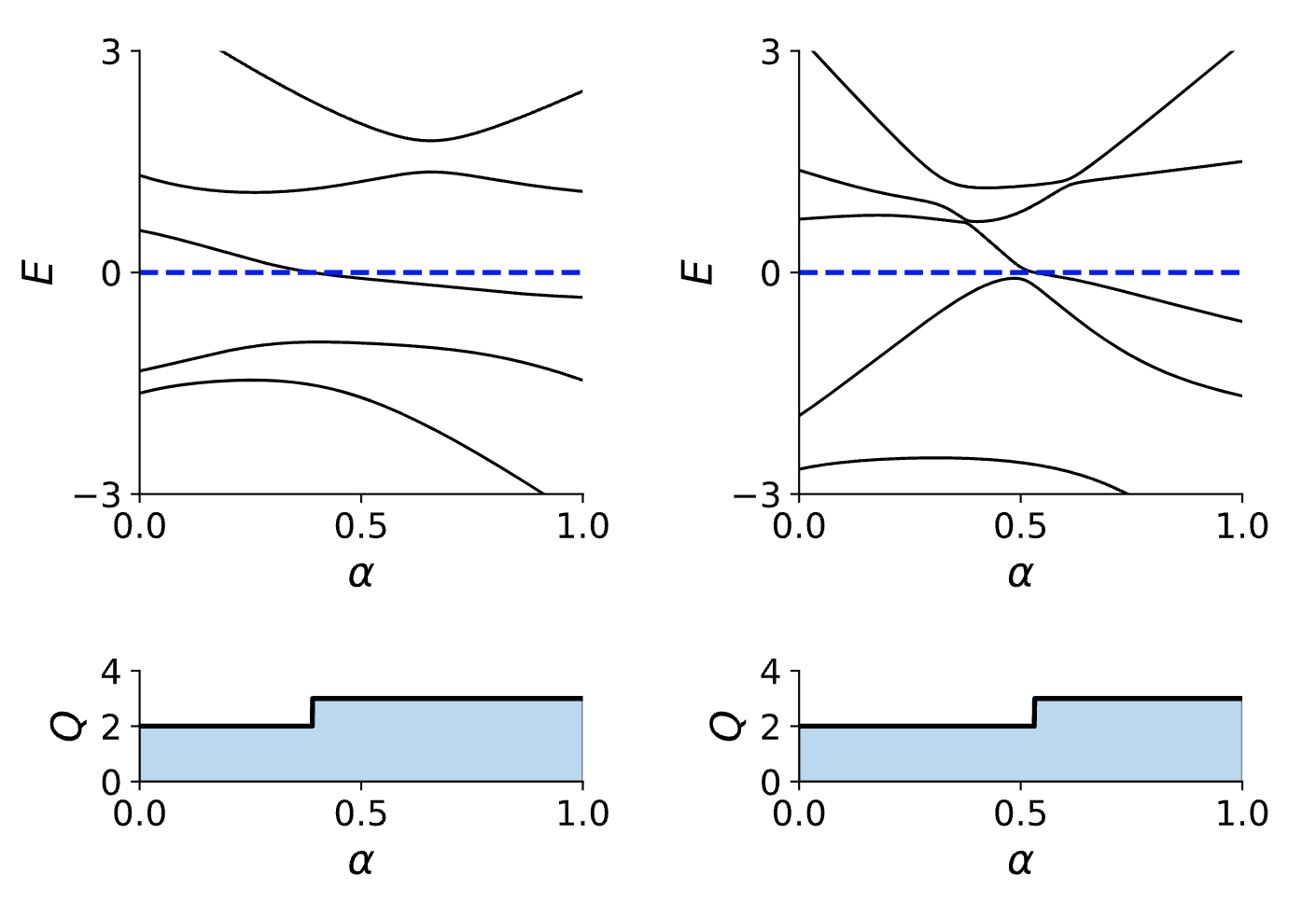
最后再将两个子块的贡献进行加和即可
可以看到当存在对称性的时候,首先会对哈密顿量产生一些限制,使得我们可以在约化的子空间中处理问题。对称性在研究拓扑的过程中是非常重要的,有时候可以仅仅通过对称性就可以判断体系是否是拓扑的。
Time-reversal symmetry
在前面的讨论中,将哈密顿量直接取为了实数,其实这种选择会暗含特定的对称性,因为一般性的考虑,并没有要求哈密顿量一定要是实数,它只要满足厄米性就可以了。对于一个矩阵元素全部都是实数的哈密顿量,它其实是满足时间反演对称性(TRS)的,TRS是一个反幺正算符,总是可以将其表示为一个幺正矩阵和复共轭操作的组合$\mathcal{T}=U\mathcal{K}$,这里的$\mathcal{K}$就是复共轭操作。对于上面讨论的实数哈密顿量,此时可以将TRS算符表示为$\mathcal{T}\equiv\mathcal{K}$,一个矩阵元素全部是实数的哈密顿量显然满足$H=H^*$。
现在往哈密顿量中加入一些复数从而破坏时间反演对称性 ![[Pasted image 20221108194017.png]] 此时发现在参数演化过程中仍然会存在能级交叉现象,而且对应的拓扑不变量会发生变化。
当考虑自旋之后,TRS会有一些不同,此时TRS算符表示为
\[\mathcal{T}=i\sigma_y \mathcal{K},\]这里的$\sigma_y$是作用在自旋自由度上面的Pauli矩阵,且满足$\mathcal{T}^2=-1$。对于spinfull的系统,如果存在时间反演对称性,此时哈密顿量满足
\[H = \sigma_y\, H^* \sigma_y.\]比如下面的这个哈密顿量就满足时间反演对称性

这种形式的哈密顿量具有以下性质:每一个本征值$E_n$都是双重简并的(Kramers简并),同样可以在上面的哈密顿量中加入任意的微扰来计算体系能级随着微扰项的变化。
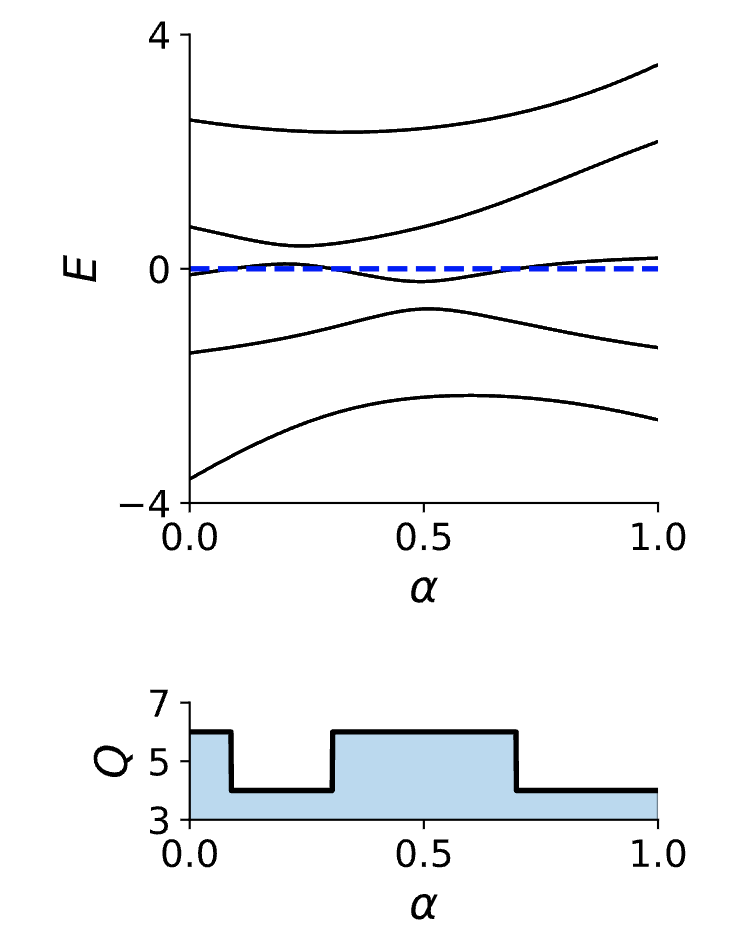
可以看到在参数演化过程中,能级与$E=0$相交的情况都是类似的,但是此时拓扑不变量的变化每次都是2而不是1。因此在这种情况下面,时间反演对称性会使得拓扑不变量只能取偶数,可以发现当系统存在对称性之后,会对体系的拓扑性质产生一定的限制。
Sublattice symmetry
上面我们看到,当存在时间反演对称性的时候,一些特定值的拓扑不变量是被禁止的,这里来研究另外一种对称性对体系拓扑性质的限制。
现在考虑一个系统,可以根据自由度将其分成两组(分别表示为A,B),只有处在A,B中的矩阵元才是非零的。当系统具有两个子晶格的时候,对应的就是上面提到的这种情况,比如graphene的原胞中就存在两个不等价的原子。此时考虑量子点系统有graphene组成
由于存在子晶格对称性,graphene量子点的哈密顿量形式为
\[H = \begin{pmatrix} 0 & H_{AB} \\ H_{AB}^\dagger & 0 \end{pmatrix}.\]同样可以通过数值的方式产生一个具有子晶格对称性的哈密顿量

这里引入一个对角的矩阵$\sigma_z$,对于格点A而言是$+1$,对于格点B而言是-1,哈密顿量满足子晶格对称性表示为
\[\sigma_z H \sigma_z = -H.\]这也就意味着,如果$(\psi_A, \psi_B)^T$是哈密顿量能量为$\epsilon$的本征态,那么$(\psi_A, -\psi_B)^T$就是能量为$-\epsilon$的本征态,因此一旦存在子晶格对称性,哈密顿量的能谱就是正负对称的。因此如果随着参数对系统进行演化,当存在子晶格对称性之后,能级与$E=0$相交的的次数一定是偶数,不会存在单独的一个能级随着时间演化与$E=0$相交。同样可以通过数值的方法构造出一个具有子晶格对称性的哈密顿量,而后计算其随着参数$\alpha$的演化
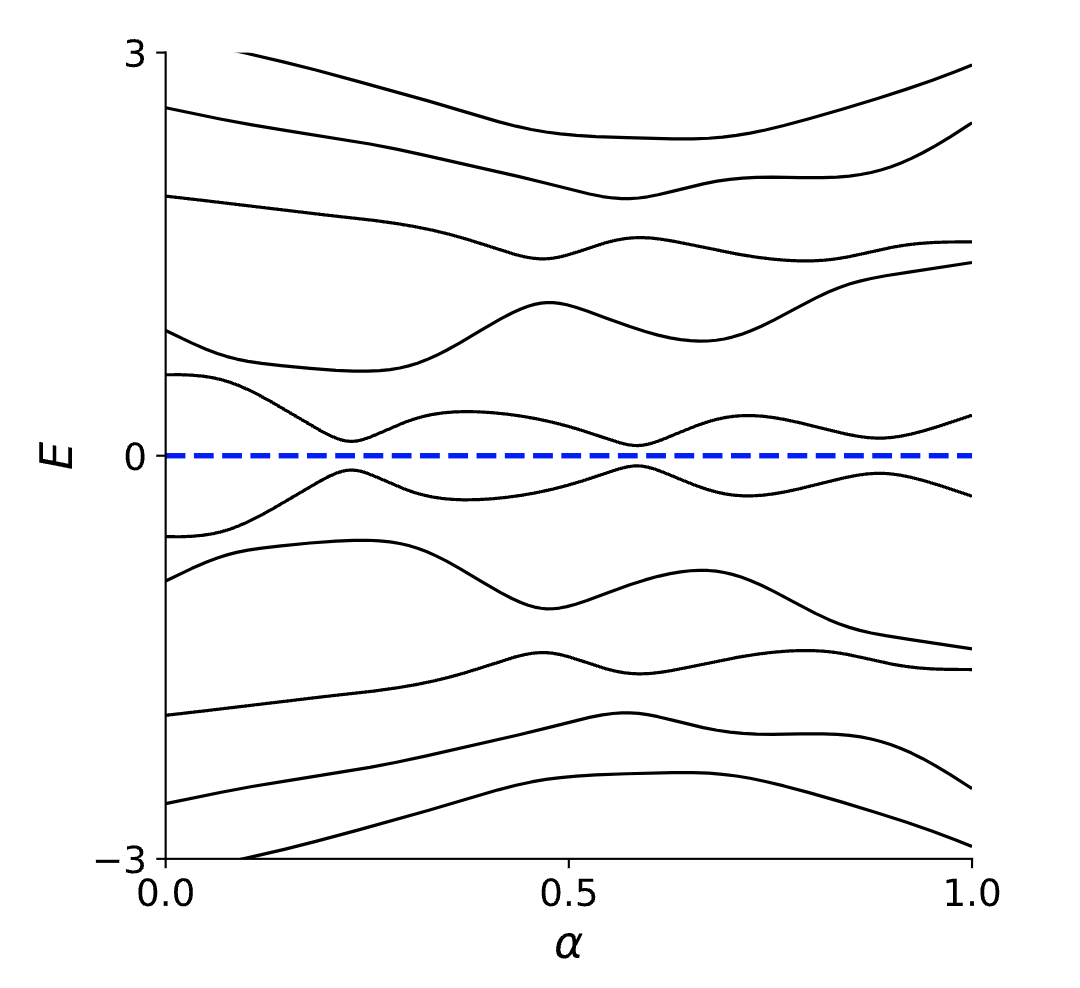
可以看到,随着参数演化并没有发生能带交叉,这也就意味着体系并没有发生拓扑相变。
Particle-hole symmetry
这里仍然有一种对称性会影响体系的拓扑:粒子空穴对称性,它通常出现在的超导体系中。如图所示,将之前所考虑的量子点体系与一个超导系统连接起来
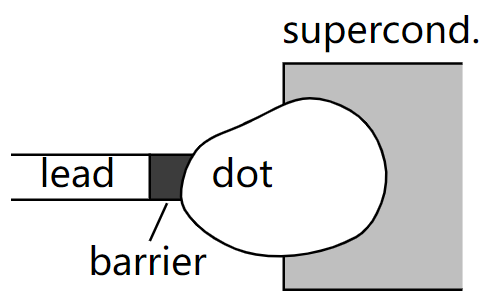
在超导体中,可以成对的产生和湮灭Cooper对,描述该超导系统的哈密顿量通常表示为
\[\mathcal{H} = \sum_{nm} H_{nm} c^\dagger_nc_m + \tfrac{1}{2} (\Delta_{nm} c^\dagger_n c^\dagger_m + \Delta^*_{nm} c_m c_n),\]这里$c^\dagger_n, c_n$是电子的产生和湮灭算符。这些算符之间满足的是反对易关系$c_nc_m+c_mc_n=0$ and $c^\dagger_n c_m + c_m c^\dagger_n = \delta_{mn}$。第一项$H$描述的是量子点系统中电子的动能项,而$\Delta$这一项描述的则是成对产生或者湮灭Cooper对。这里的矩阵$\Delta$是反对称的,因此此时费米子算符之间满足的是反对易关系。此时可以发现哈密顿量$\mathcal{H}$描述的系统,电子数并不是守恒的,但是电子数目对应的宇称是一个守恒量,因为他们都是成对产生或者成对湮灭的。现在可以把产生算符和湮灭算符整理到一起表示为矢量形式$C = (c_1, \dots, c_n, c^\dagger_1, \dots, c^\dagger_n)^T$,那么就可以将$\mathcal{H}$表示为矩阵对矢量进行运算的形式
\[\mathcal{H} = \frac{1}{2} C^\dagger H_\textrm{BdG}\,C\,.\]矩阵$H_{\rm BdG}$就是Bogoliubov-de Gennes哈密顿量(BdG),它的矩阵形式为
\[H_\textrm{BdG} = \begin{pmatrix} H & \Delta \\ -\Delta^* & -H^* \end{pmatrix}.\]在BdG哈密顿量中,上半部分是由电子的湮灭算符组成的,而剩下的部分则是由相同电子的产生算符组成的。可以将其等效的看做是一系列额外空穴的湮灭算符。所以在这样的系统中,其实是存在冗余自由度的。因为电子和空穴是相互联系的,$H_{\rm BdG}$天然的具有额外的对称性,这个对称性会将电子交换称为空穴,且同样是一个反幺正的操作$\mathcal{P}=\tau_x\mathcal{K}$,这里的Pauli矩阵$\tau_x$是作用在粒子和空穴block上的,此时哈密顿量和对称操作算符之间满足
\[\mathcal{P} H_\textrm{BdG} \mathcal{P}^{-1} = -H_\textrm{BdG}.\]粒子空穴对称性是一个反幺正的操作,它与哈密顿量之间满足反对易关系。因为此时反对易会出现一个负号,所以$H_{\rm BdG}$的能谱一定是关于$E=0$正负对称的。如果$\psi = (u, v)^T$是$H_{\rm BdG}$能量为$E$的本征态,那么$\mathcal{P}\psi=(v^, u^)^T$就是能量为$-E$的本征态。
这里其实可以看到,粒子空穴对称性与子晶格对称性与哈密顿量满足的都是反对易关系,系统的能谱也都是关于$E=0$正负对称的,但是粒子空穴对称性是反幺正操作,同时包含了一个复共轭操作$\mathcal{K}$,而子晶格对称性则是幺正对称性。
此时同样产生一个BdG哈密顿量
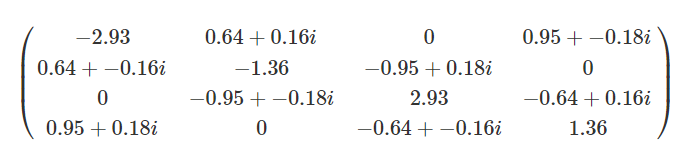
此时演化参数$\alpha$来观察系统的能级是如何发生变化的
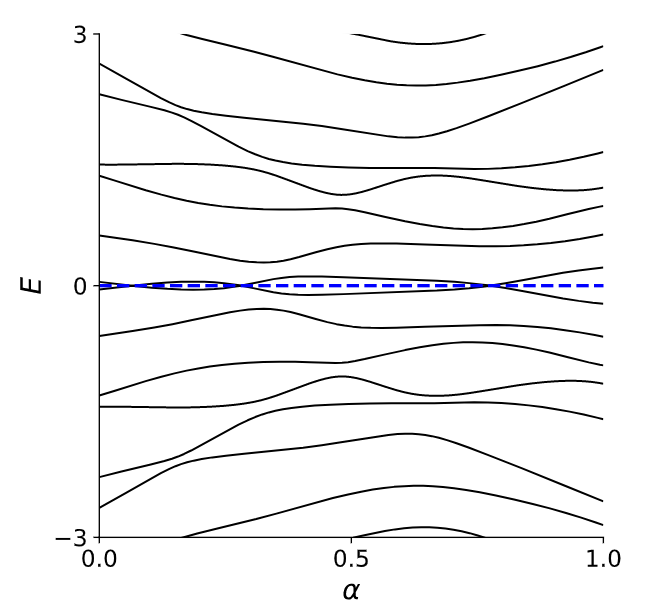
可以看到能谱始终关于$E=0$对称的,而且此时$E<0$和$E>0$的能级是可以发生交叉的,而在子晶格对称性的情形下,能级始终没有发生交叉,虽然能谱也是关于$E=0$正负对称的。
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |

