png

Andreev反射作为超导独特的性质，在很多方面都有独特的现象，最近学习相关方面的知识，这里就先整理了一下。
{:.info}

Andreev Reflection

考虑如上图所示的正常态-超导异质结，沿着$x$方向标记为纵向方向，将$(y,z)$方向标记为横向。两种不同属性的交界面位于$x=0$处，这个系统对应的BdG方程为

$\left(\begin{array}{cc} \mathcal{H}_{e} & \Delta \\ \Delta^{*} & -\mathcal{H}_{e}^{*} \end{array}\right)\left(\begin{array}{l} u \\ v \end{array}\right)=E\left(\begin{array}{l} u \\ v \end{array}\right)$

这个junction中的超导序参量就是阶跃函数的形式

$\Delta(x)=\Theta(x)\Delta_0 e^{i\varphi}$

这里假设系统沿着纵向和横向是可分离的，那么可以将波函数分解为纵向部分和横向部分

$\begin{equation} \Psi(x,y,z)=\psi(x)\Phi_n(y,z)\left\{ \begin{array}{c} \psi(x)\quad\rightarrow\text{纵向波函数}\\ \Phi_n(y,z)\quad\rightarrow\text{横向波函数} \end{array} \right. \end{equation}$

这里$n$表示横向模式量子数，满足

$[-\frac{\hbar^2}{2m}(\frac{\partial^2}{\partial z^2}+\frac{\partial^2}{\partial y^2})+V_\perp(y,z)]\Phi_n(y,z)=E_n\Phi_n(y,z)$

这里的$E_n$就是横向模式的能量，$V_\perp$表示横向囚禁势。

由于系统在纵向和横向是分开的，那么此时能量也可以分成纵向与横向

$E=E_\parallel+E_n$

对于一个给定的横向模式$n$，可以得到纵向传播模式的有效化学势为

$\epsilon_{F_n}=\epsilon_F-E_n$

这里假设了化学势$\epsilon_F$中包含了自洽势U。

为了考虑界面上的接触电阻，在边界上加入一个势$\Gamma\delta(x)$。

结合上面的这些描述，系统可以被一个有效的1D BdG哈密顿量描述

$\left(\begin{array}{cc} -\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}-\varepsilon_{F n}+\Lambda \delta(x) & \Delta(x) \\ \Delta^{*}(x) & \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+\varepsilon_{F n}-\Lambda \delta(x) \end{array}\right)\left(\begin{array}{c} u(x) \\ v(x) \end{array}\right)=E\left(\begin{array}{c} u(x) \\ v(x)\label{q1} \end{array}\right)$

这里就是Blonder-Tinkham-Klapwijk(BTK)模型。接下来就是求解$E\geq 0$对应的解。

正常态区域

在正常态区域，因为不存在电子配对，方程\eqref{q1}约化为

$\left(\begin{array}{cc} -\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}-\varepsilon_{F n} & 0 \\ 0 & \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+\varepsilon_{F n} \end{array}\right)\left(\begin{array}{c} u(x) \\ v(x) \end{array}\right)=E\left(\begin{array}{c} u(x) \\ v(x)\label{q2} \end{array}\right)$

方程\eqref{q2}有两个粒子解

$\Psi_{\pm}^{e}(x)=\left(\begin{array}{c} 1 \\ 0 \end{array}\right) e^{\pm i k_{e} x}\quad k_e=k_{F_n}\sqrt{1+\frac{E}{\epsilon_{F_n}}},\quad k_{F_n}=\frac{\sqrt{2m\epsilon_{F_n}}}{\hbar}$

两个空穴解

$\Psi_{\pm}^{h}(x)=\left(\begin{array}{c} 0 \\ 1 \end{array}\right) e^{\pm i k_{h} x}\quad k_h=k_{F_n}\sqrt{1-\frac{E}{\epsilon_{F_n}}},\quad k_{F_n}=\frac{\sqrt{2m\epsilon_{F_n}}}{\hbar}$

png

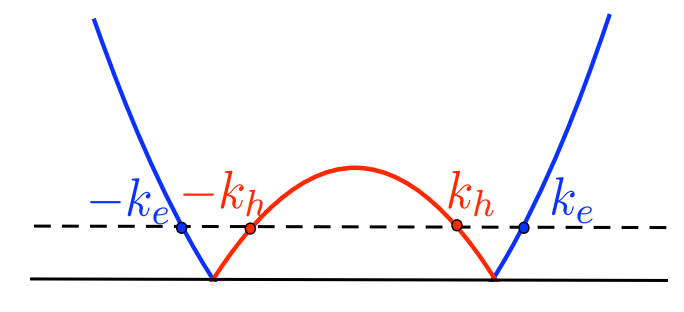
正常态区域的能谱如图所示。

超导态区域

在超导区域，存在电子配对，方程\eqref{q1}约化为

$\left(\begin{array}{cc} -\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}-\varepsilon_{F n} & \Delta_{0} e^{i \varphi} \\ \Delta_{0} e^{-i \varphi} & \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+\varepsilon_{F n} \end{array}\right)\left(\begin{array}{c} u(x) \\ v(x) \end{array}\right)=E\left(\begin{array}{c} u(x) \\ v(x) \end{array}\right)$

因为超导侧是存在能隙的，所以此时根据能量$E$与电子配对$\Delta_0$的大小，存在两种情况。

png

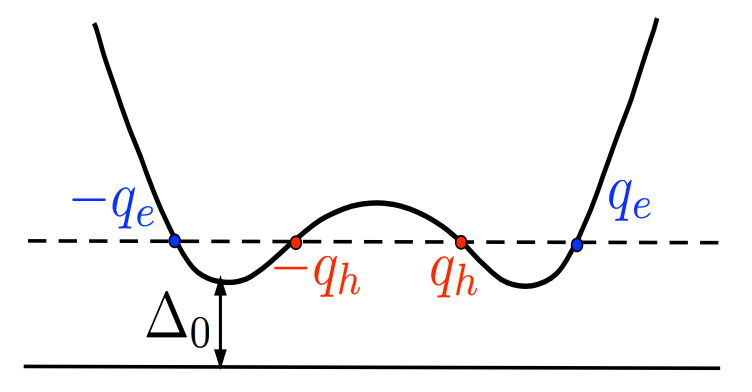
Supra-gap solutions($E>\Delta_0$): propagating waves

当能量$E>\Delta_0$的时候，存在两个类粒子解

$\Psi_{\pm}^{e}(x)=\left(\begin{array}{c} u_{0} e^{i \varphi / 2} \\ v_{0} e^{-i \varphi / 2} \end{array}\right) e^{\pm i q_{e} x}\quad q_e=k_{F_n}\sqrt{1+\sqrt{\frac{E^2-\Delta_0^2}{\epsilon_{F_n}^2}}},\quad k_{F_n}=\frac{\sqrt{2m\epsilon_{F_n}}}{\hbar}$

和两个类空穴解

$\Psi_{\pm}^{h}(x)=\left(\begin{array}{c} v_{0} e^{i \varphi / 2} \\ u_{0} e^{-i \varphi / 2} \end{array}\right) e^{\pm i q_{h} x}\quad q_h=k_{F_n}\sqrt{1-\sqrt{\frac{E^2-\Delta_0^2}{\epsilon_{F_n}^2}}},\quad k_{F_n}=\frac{\sqrt{2m\epsilon_{F_n}}}{\hbar}$

这里$u_0,v_0$分别为

$\begin{array}{l} u_{0}=\sqrt{\frac{1}{2}\left(1+\sqrt{1-\left(\frac{\Delta_{0}}{E}\right)^{2}}\right)} \equiv \sqrt{\frac{\Delta_{0}}{2 E}} e^{\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} \\ v_{0}=\sqrt{\frac{1}{2}\left(1-\sqrt{1-\left(\frac{\Delta_{0}}{E}\right)^{2}}\right)} \equiv \sqrt{\frac{\Delta_{0}}{2 E}} e^{-\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} \end{array}$

将其带入可以得到两个类粒子解为

$\Psi_{\pm}^{e}(x)=\sqrt{\frac{\Delta_{0}}{2 E}}\left(\begin{array}{c} e^{\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} e^{i \varphi / 2} \\ e^{-\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} e^{-i \varphi / 2} \end{array}\right) e^{\pm i q_{e} x}$

两个类空穴解为

$\Psi_{\pm}^{h}(x)=\sqrt{\frac{\Delta_{0}}{2 E}}\left(\begin{array}{c} e^{-\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} e^{i \varphi / 2} \\ e^{\frac{1}{2} \operatorname{arccosh} \frac{E}{\Delta_{0}}} e^{-i \varphi / 2} \end{array}\right) e^{\pm i q_{h} x}$

Sub-gap solutions($E<\Delta_0$): evanescent waves

当能量$E<\Delta_0$的时候，$q_{e/h}$均会获得虚数部分

$\begin{array}{l} q_{e}=k_{F n} \sqrt{1+i \sqrt{\frac{\Delta_{0}^{2}-E^{2}}{\varepsilon_{F n}^{2}}}} \\ q_{h}=k_{F n} \sqrt{1-i \sqrt{\frac{\Delta_{0}^{2}-E^{2}}{\varepsilon_{F n}^{2}}}} \end{array}$

类似的可以得到$u_0,v_0$

$\begin{array}{l} u_{0}=\sqrt{\frac{\Delta_{0}}{2 E}} e^{\frac{i}{2} \arccos \frac{E}{\Delta_{0}}} \\ v_{0}=\sqrt{\frac{\Delta_{0}}{2 E}} e^{-\frac{i}{2} \arccos \frac{E}{\Delta_{0}}} \end{array}$

在这种情况下有$\rvert u_0\rvert^2+\rvert v_0\rvert^2\neq1$，但是有

$\begin{aligned} u_0^2+v_0^2&=\frac{\Delta_0}{2E}(e^{i\arccos\frac{E}{\Delta_0}}+e^{-i\arccos\frac{E}{\Delta_0}})\\ &=\frac{\Delta_0}{2E}2\cos(\arccos\frac{E}{\Delta_0})=1 \end{aligned}$

边界条件

将方程

$-\frac{\hbar^2}{2m}\frac{\partial^2u}{\partial x^2}-\epsilon_{F_n}u(x)+\Gamma\delta(x)u(x)+\Delta(x)v(x)=Eu(x)$

在$x=0$处进行积分，就可以得到边界条件

$\begin{aligned} &\partial_xu(0^+)-\partial_xu(0^-)=\frac{2m\Gamma}{\hbar^2}u(0)\\ &\partial_xv(0^+)-\partial_xv(0^-)=\frac{2m\Gamma}{\hbar^2}v(0)\\ \end{aligned}$

散射矩阵系数

接下来求解散射矩阵的系数，首先考虑从正常态区域向交界面入射电子

$\Psi_{\rm in}(x)=\frac{1}{\sqrt{2\pi\hbar v_e}}\left( \begin{array}{c} 1\\ 0 \end{array} \right)e^{+ik_ex}$

反射回正常态区域的波函数为向左传播的电子或者向左传播的空穴

$\Psi_{\rm refl}=\frac{r_{\rm ee}}{2\pi\hbar v_e}\left( \begin{array}{c} 1\\ 0 \end{array} \right)e^{-ik_ex}+\frac{r_{\rm he}}{2\pi\hbar v_h}\left( \begin{array}{c} 0\\ 1 \end{array} \right)e^{+ik_hx}$

相反，透射波是向右移动的类电子解或者向右移动的类空穴解

$\Psi_{t r a n s}(x)=\frac{t_{e e}}{\sqrt{2 \pi \hbar w_{e}}}\left(\begin{array}{c} u_{0} e^{i \varphi / 2} \\ v_{0} e^{-i \varphi / 2} \end{array}\right) e^{+i q_{e} x}+\frac{t_{h e}}{\sqrt{2 \pi \hbar w_{h}}}\left(\begin{array}{c} v_{0} e^{i \varphi / 2} \\ u_{0} e^{-i \varphi / 2} \end{array}\right) e^{-i q_{h} x}$

这里我们标记了

$\begin{aligned} &r_{ee}=\text{反射系数}\quad e\rightarrow e\\ &r_{he}=\text{反射系数}\quad e\rightarrow h\\ &t_{ee}=\text{透射系数}\quad e\rightarrow e\\ &t_{he}=\text{透射系数}\quad e\rightarrow h\\ \end{aligned}$

我们已经将波函数与它们的速度归一化，因为它们对于粒子和空穴来说通常是不同的，从普通面到超导面也是不同的。这样，每个波函数携带了相同数量的准粒子概率电流的通量，因此上述系数描述了一个幺正矩阵。我们回顾了散射矩阵的幺正性源于准粒子概率电流的守恒。

对于正常态一侧有

$\begin{array}{l} E=\frac{\hbar^{2} k_{e}^{2}}{2 m}-\varepsilon_{F n} \quad \Rightarrow \quad v_{e}=\frac{1}{\hbar}\left|\frac{d E}{d k_{e}}\right|=\frac{\hbar k_{e}}{m} \\ E=\varepsilon_{F n}-\frac{\hbar^{2} k_{h}^{2}}{2 m} \quad \Rightarrow \quad v_{h}=\frac{1}{\hbar}\left|\frac{d E}{d k_{h}}\right|=\frac{\hbar k_{h}}{m} \\ \end{array}$

对于超导一侧有

$\begin{aligned} E & =\sqrt{\left(\frac{\hbar^{2} q_{e}^{2}}{2 m}-\varepsilon_{F n}\right)^{2}+\Delta_{0}^{2}} & \Rightarrow & w_{e}=\frac{1}{\hbar}\left|\frac{d E}{d q_{e}}\right|=\frac{\hbar q_{e}}{m} \\ E & =\sqrt{\left(\varepsilon_{F n}-\frac{\hbar^{2} q_{h}^{2}}{2 m}\right)^{2}+\Delta_{0}^{2}} & \Rightarrow & w_{h}=\frac{1}{\hbar}\left|\frac{d E}{d q_{h}}\right|=\frac{\hbar q_{h}}{m} \end{aligned}$

速度为

$\begin{aligned} v_{e/h}&=\frac{\hbar k_{e/h}}{m}\\ w_{e/h}&=\frac{\sqrt{E^2-\Delta_0^2}}{E}v_{e/h}=(u_0^2-v_0^2)v_{e/h} \end{aligned}$

对于反射波，电子和空穴具有相反符号的动量，仅仅是因为我们想要描述向左运动的波，对于向右运动的波也是类似的

png

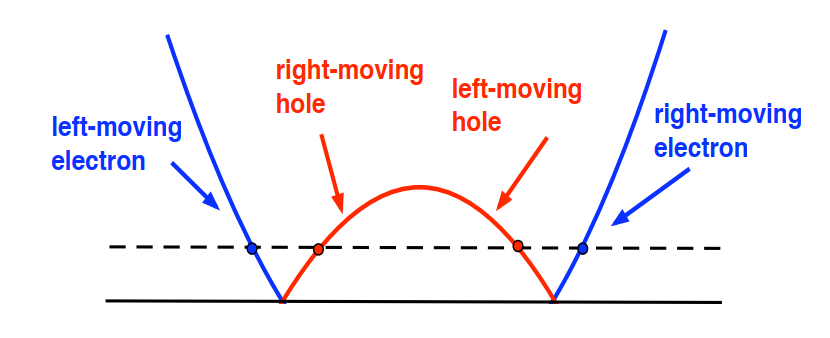
为了得到解，这里采用

$\begin{aligned} u(0^+)&=u(0^-)\\ v(0^+)&=v(0^-)\\ \partial_xu(0^+)-\partial_xu(0^-)&=\frac{2m\Gamma}{\hbar^2}u(0)\\ \partial_xv(0^+)-\partial_xv(0^-)&=\frac{2m\Gamma}{\hbar^2}v(0) \end{aligned}$

上面的这些条件就会得到一系列关于$r_{ee},r_{he},t_{ee},t_{he}$的未知方程。通过求解方程得到这些系数，利用散射矩阵的幺正性可以得到其他的系数，比如$r_{eh},t_{eh}$等。

Andreev近似下的解

线性方程组的显式解在Andreev近似中特别简单，它包括设想相对于费米能级的低能量

$E,\Delta_0\ll\epsilon_{F_n}$

在这个近似下面可以得到

$\begin{aligned} &k_{e/h}\simeq q_{e/h}\simeq k_{F_n}\\ &v_{e/h}\simeq v_{F_n}\\ &w_{e/h}\simeq\frac{\sqrt{E^2-\Delta_0^2}}{E}v_{F_n}=(u_0^2-v_0^2)v_{F_n} \end{aligned}$

这里费米速度的定义为

$v_{F_n}=\frac{\hbar k_{F_n}}{m}$

在Andreev近似下面可以得到，对于透射与反射振幅有

$\begin{aligned} r_{h e} & =\frac{u_{0} v_{0}}{u_{0}^{2}+Z^{2}\left(u_{0}^{2}-v_{0}^{2}\right)} e^{-i \varphi} \\ r_{e e} & =\frac{\left(Z^{2}+i Z\right)\left(v_{0}^{2}-u_{0}^{2}\right)}{u_{0}^{2}+Z^{2}\left(u_{0}^{2}-v_{0}^{2}\right)} \\ t_{e e} & =\frac{(1-i Z) u_{0} \sqrt{u_{0}^{2}-v_{0}^{2}}}{u_{0}^{2}+Z^{2}\left(u_{0}^{2}-v_{0}^{2}\right)} e^{-i \varphi / 2} \\ t_{h e} & =\frac{i Z v_{0} \sqrt{u_{0}^{2}-v_{0}^{2}}}{u_{0}^{2}+Z^{2}\left(u_{0}^{2}-v_{0}^{2}\right)} e^{-i \varphi / 2} \end{aligned}$

这里

$Z=\frac{\Gamma m}{\hbar^2 k_{F_n}}=\frac{\Gamma}{\hbar v_{F_n}}$

是BKT模型中一个无量纲的参数用来标记界面的透明度

$\left\{ \begin{array}{c} Z\ll 1\quad \text{非常透明的界面}\\ Z\gg 1\quad \text{弱透明界面(隧穿极限)} \end{array} \right.$

这里的透明性指的是正常态情况下，即当超导侧的间隙设为零($\Delta_0\rightarrow 0$)或温度高于临界温度$T_c$。通过这个关系可以证明BTK参数与$T_N$是相关的

$T_N=\frac{1}{1+Z^2}$

对应的透射和反射系数为

$\begin{array}{l} A \doteq A_{L L}^{h e} \doteq\left|r_{h e}\right|^{2} \\ B \doteq A_{L L}^{e e} \doteq\left|r_{e e}\right|^{2} \\ C \doteq A_{R L}^{e e} \doteq\left|t_{e e}\right|^{2} \\ D \doteq A_{R L}^{h e} \doteq\left|t_{h e}\right|^{2} \end{array}$

回顾前面在$E>\Delta_0$和$E<\Delta_0$情况下$u_0$和$v_0$的关系，可以得到

Supra-gap($E>\Delta_0$)

$\begin{array}{l} A(E)=A_{L L}^{h e}(E)=\frac{\Delta_{0}^{2}}{\left(E+\left(1+2 Z^{2}\right) \sqrt{E^{2}-\Delta_{0}^{2}}\right)^{2}} \\ B(E)=A_{L L}^{e e}(E)=\frac{4 Z^{2}\left(1+Z^{2}\right)\left(E^{2}-\Delta_{0}^{2}\right)}{\left(E+\left(1+2 Z^{2}\right) \sqrt{E^{2}-\Delta_{0}^{2}}\right)^{2}} \\ C(E)=A_{R L}^{e e}(E)=\frac{2\left(1+Z^{2}\right) \sqrt{E^{2}-\Delta_{0}^{2}}\left(E+\sqrt{E^{2}-\Delta_{0}^{2}}\right)}{\left(E+\left(1+2 Z^{2}\right) \sqrt{E^{2}-\Delta_{0}^{2}}\right)^{2}} \\ D(E)=A_{R L}^{h e}(E)=\frac{2 Z^{2} \sqrt{E^{2}-\Delta_{0}^{2}}\left(E-\sqrt{E^{2}-\Delta_{0}^{2}}\right)}{\left(E+\left(1+2 Z^{2}\right) \sqrt{E^{2}-\Delta_{0}^{2}}\right)^{2}} \end{array}$

我们可以验证

$\sum_{J=L/R}\sum_{\beta=e/h}A_{JL}^{\beta e}=1\xLeftrightarrow{} A+B+C+D=1$

这同样也是S矩阵幺正性所要求的。

Sub-gap($E<\Delta_0$)

$\begin{array}{l} A(E)=A_{L L}^{h e}=\left|r_{h e}\right|^{2}=\frac{\Delta_{0}^{2}}{E^{2}+\left(1+2 Z^{2}\right)^{2}\left(\Delta_{0}^{2}-E^{2}\right)} \\ B(E)=A_{L L}^{e e}=\left|r_{e e}\right|^{2}=\frac{4 Z^{2}\left(1+Z^{2}\right)\left(\Delta_{0}^{2}-E^{2}\right)}{E^{2}+\left(1+2 Z^{2}\right)^{2}\left(\Delta_{0}^{2}-E^{2}\right)} \\ C(E)=A_{R L}^{e e}=\left|t_{e e}\right|^{2}=0 \\ D(E)=A_{R L}^{h e}=\left|t_{h e}\right|^{2}=0 \end{array}$

注意到，在subgap情形下，透射系数均为零$C=D=0$，此时可以验证

$\sum_{J=L/R}\sum_{\beta=e/h}A^{\beta e}_{JL}=1\qquad\xLeftrightarrow{}\qquad A+B=1$

Andreev Reflection

理想界面($Z=0$)

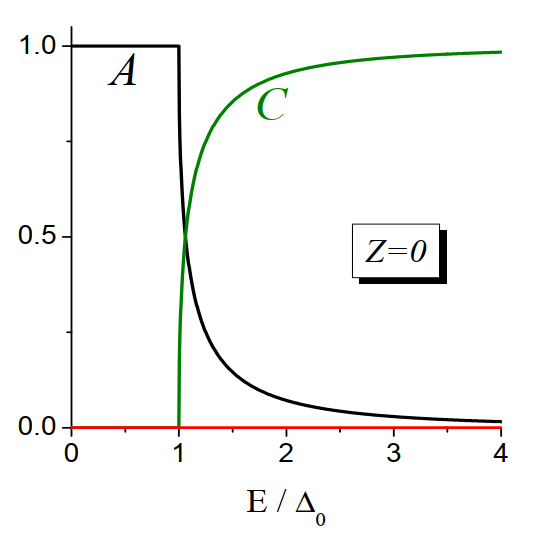
为了讨论前面计算得到的系数$A,B,C,D$的物理含义，这里首先考虑理想界面($Z=0$)，此时对于$e\rightarrow h$的Andreev反射振幅为

$r_{he}=\frac{v_0}{u_0}e^{-i\varphi}=e^{-\varphi}\left\{ \begin{array}{c} e^{-i\arccos\frac{E}{\Delta_0}}\quad E<\Delta_0\\ e^{-\arccos\frac{E}{\Delta_0}}\quad E>\Delta_0 \end{array} \right.$

类似的对于$h\rightarrow e$的过程对应的系数为

$r_{eh}=\frac{v_0}{u_0}e^{i\varphi}=e^{-\varphi}\left\{ \begin{array}{c} e^{-i\arccos\frac{E}{\Delta_0}}\quad E<\Delta_0\\ e^{-\arccos\frac{E}{\Delta_0}}\quad E>\Delta_0\\ \end{array} \right.$

对应的系数为

Sub-gap区域($E<\Delta_0$)

$\begin{aligned} A(E)&=1\\ B(E)&=0\\ C(E)&=0\\ D(E)&=0 \end{aligned}$

这表明在正常金属-超导(NS)界面处，一个入射电子只能通过Andreev反射为空穴，而且反射几率为100%，这个现象就叫做Andreev反射，如下图所示

png

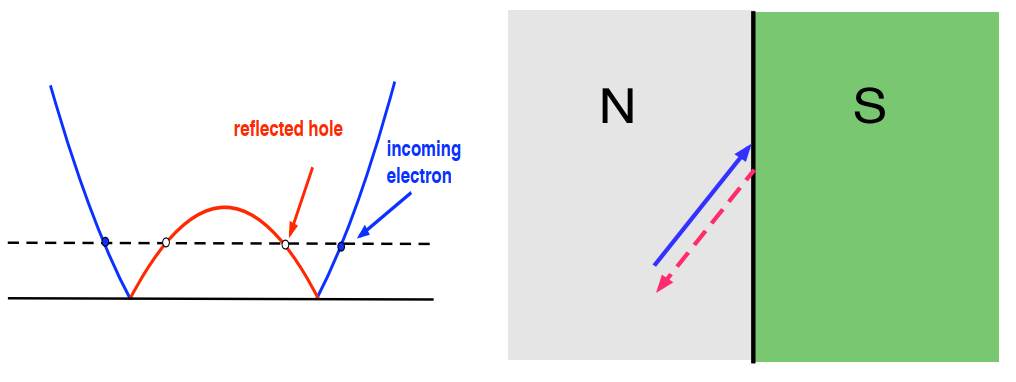
对于正常的反射，动量是不守恒的，但是电荷守恒。而对于Andreev反射，动量是近似守恒的(入射电子和反射空穴具有非常靠近$k_F$的动量)，重要的是它们速度的方向是相反的。

Supra-gap区域($E>\Delta_0$)

$\begin{aligned} A(E) & =\frac{\Delta_{0}^{2}}{\left(E+\sqrt{E^{2}-\Delta_{0}^{2}}\right)^{2}} \\ B(E) & =0 \\ C(E) & =\frac{2 \sqrt{E^{2}-\Delta_{0}^{2}}}{E+\sqrt{E^{2}-\Delta_{0}^{2}}} \\ D(E) & =0 \end{aligned}$

从这里可以看到，当能量大于超导能隙的时候，电子就有一定的几率透射称为电子，因为在超导能隙以上是由单粒子态可以占据的。当能量$E\gg\Delta_0$的时候，超导效应和正常传输实际上是最可能的过程，如下图所示($C(E)$曲线)

png

非理想界面($Z>0$)

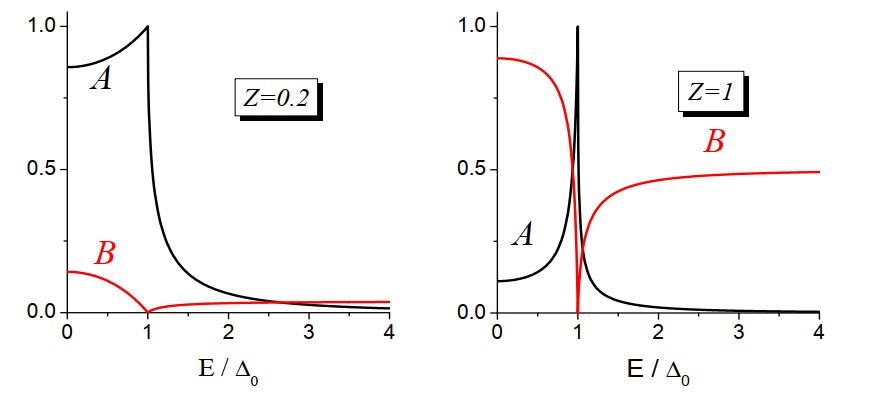
接下来考虑非理想界面的情况，此时入射电子仍然是有一定的几率反射为空穴的，但是在这种情况下，因为有界面势垒的存在，入射电子同样可以原路返回为电子。在sub-gap区域这两个过程的几率和一定等于1($A+B=1$)，所以正常的电子反射几率的增加会导致Andreev反射几率的降低，如下图所示，给出了不同$Z$时的系数$A,B$随着$E$的变化

png

电流电压特征

在连接到正常态电极的输运测量中，电流的Landauer-Buttiker公式为

$I=\frac{2 e^{2}}{h} \int d E \underbrace{T(E)}_{=1-R(E)}\left(f_{L}(E)-f_{R}(E)\right)$

这里$T(E)$时样品的透射系数，$R(E)$为反射系数，前面的$2$为自旋煎饼，$f_{L/R}(E)$分别时左右两端源的费米分布函数

$f_X(E)=\frac{1}{1+e^{(E-\mu_X)/k_BT}}\quad X=L/R$

对于接管样品连接一个正常态和超导态电极的时候，公式变为

$I=\frac{2e^2}{h}\int dE(1-B(E)+A(E))(f_L(E)-f_R(E))$

这里

$B=\rvert r^{ee}\rvert$为正常反射系数，它会减小电流
$A=\rvert r^{he}\rvert$为Andreev反射系数，它会增加电流

当温度$T=0$时有

$I=\frac{2e^2}{h}\int_0^VdE(1-B(E)+A(E))$

这里设置

$\mu_L=\epsilon_F+eV,\qquad \mu_R=\epsilon_F,\qquad V>0$

零温时的非线性电导为

$G_{\rm NS}=\frac{dI}{dV}=\frac{2e^2}{h}(1-B(eV)+A(eV))$

将系数带入可得

$G_{\mathrm{NS}}(V)=\frac{2 e^{2}}{h}\left\{\begin{array}{ll} \frac{2 \Delta_{0}^{2}}{(e V)^{2}+\left(1+2 Z^{2}\right)^{2}\left(\Delta_{0}^{2}-(e V)^{2}\right)} & e V<\Delta_{0} \\ \frac{2 \mathrm{eV}}{e V+\left(1+2 Z^{2}\right) \sqrt{(e V)^{2}-\Delta_{0}^{2}}} & e V>\Delta_{0} \end{array}\right.$

在subgap区域$eV\leq\Delta_0$因为幺正性有$A+B=1$，所以有

$G_{\rm NS}(V\leq\Delta_0)=\frac{4e^2}{h}A(eV)$

在高电压情况下($eV\gg \Delta_0$)，此时超导效应可以忽略，可以得到正常态的电导(等价于$\Delta_0\rightarrow 0$)

$G_{\rm NS}(eV\gg\Delta_0)\rightarrow G_{\rm NN}=\frac{2e^2}{h}\frac{1}{1+Z^2}$

从这里可以得到界面上正常态的透射系数为

$T_N=\frac{1}{1+Z^2}$

知道了电导，可以等价的得到界面上的电阻

$R_N=G_{\rm NN}^{-1}=\frac{h}{2e^2}(1+Z^2)$

png

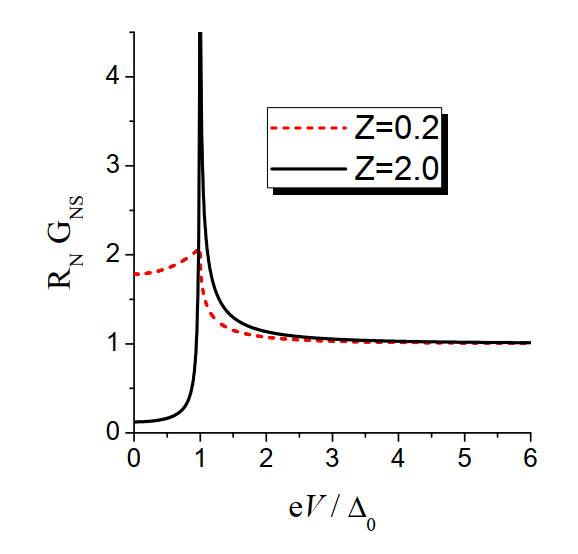
非线形电导如上图所示：

对于高透明度情形，在subgap区域主要发生的是Andreev过程($A\simeq 1$)，所以$G_{\rm NS}$是有限的；而对于低透明度的界面，Andreev反射被抑制，正常态反射占据主导，此时$G_{\rm NS}$受到抑制。
在$eV=\Delta_0$时，$G_{\rm NS}(V)$会出现一个尖峰，对应的正好就是超导体在能隙边上态密度发散位置。