库仑势以及屏蔽库伦势的一些计算

整理一下将库仑势以及屏蔽库仑势通过Fourier变换到实空间时的衰减情况
{:.info}

库伦势

如果电子之间是直接的库伦相互作用，

$$V(\boldsymbol{k})=\frac{1}{|\boldsymbol{k}|}$$

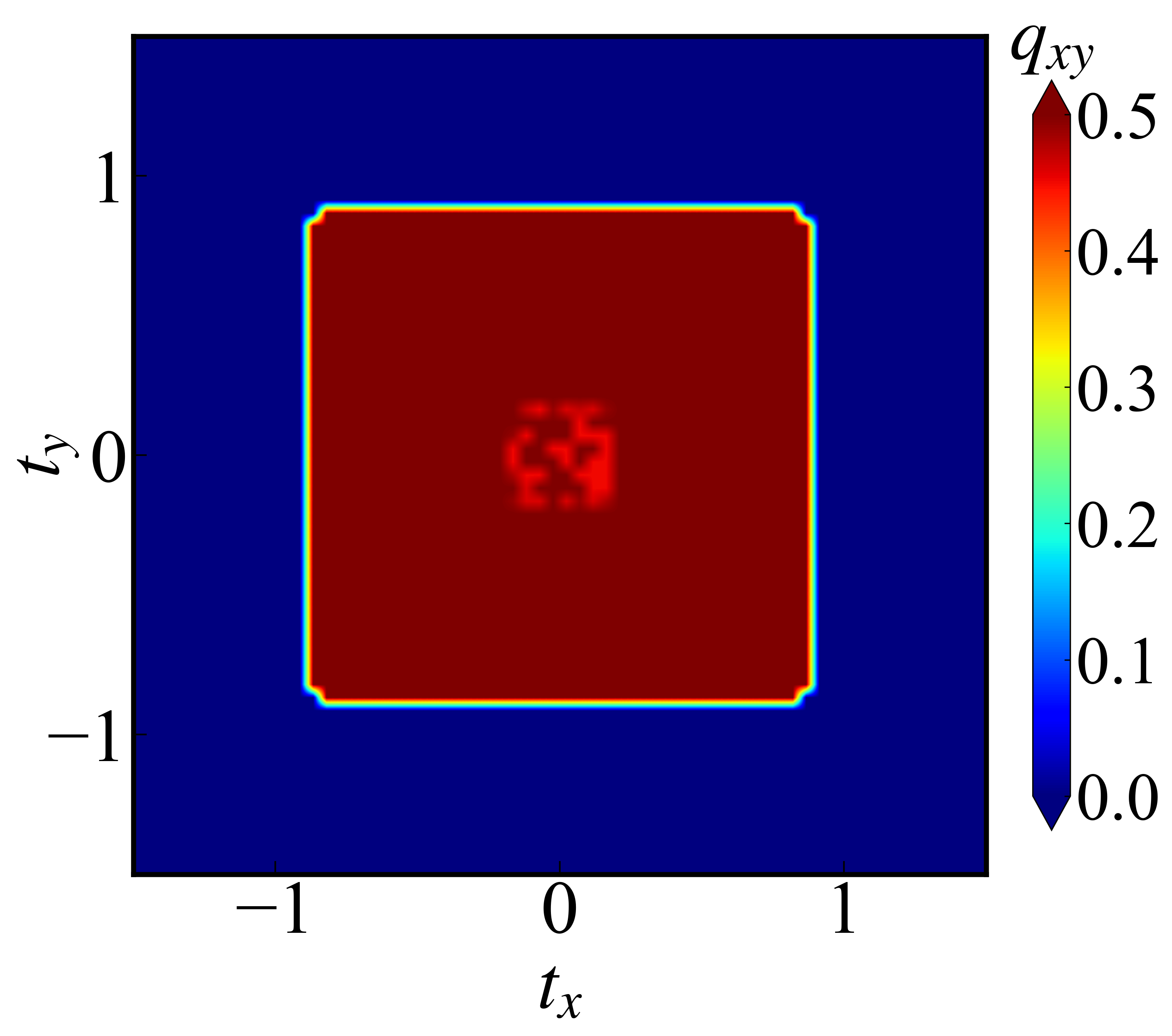
该势能随着$\rvert \boldsymbol{k}\rvert $增加而减小，如下图所示

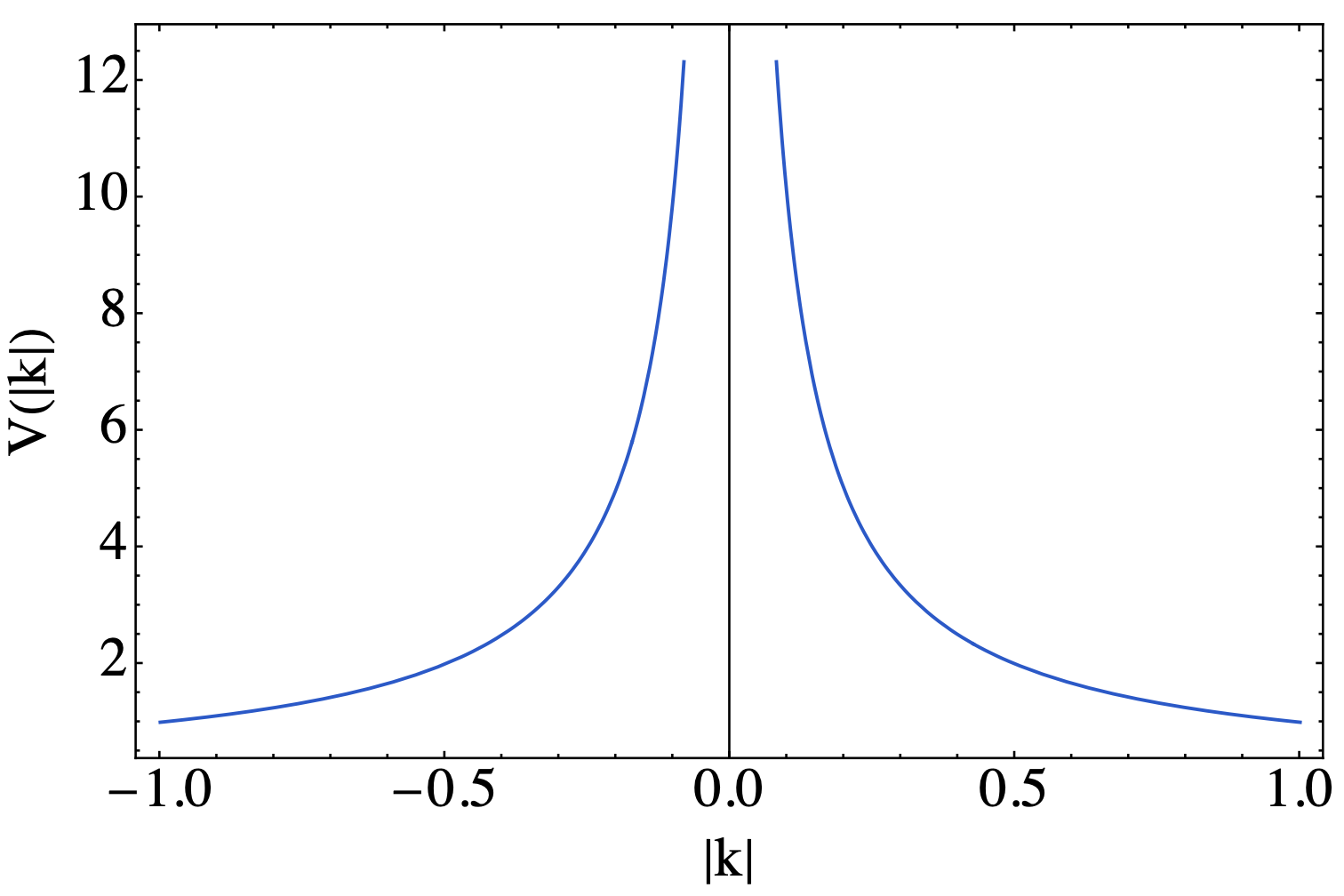
通过Fourier变换到实空间中

$$V(\boldsymbol{r})=\sum_{\boldsymbol{k}}V(\boldsymbol{k})e^{i(\boldsymbol{k}\cdot \boldsymbol{r})}$$

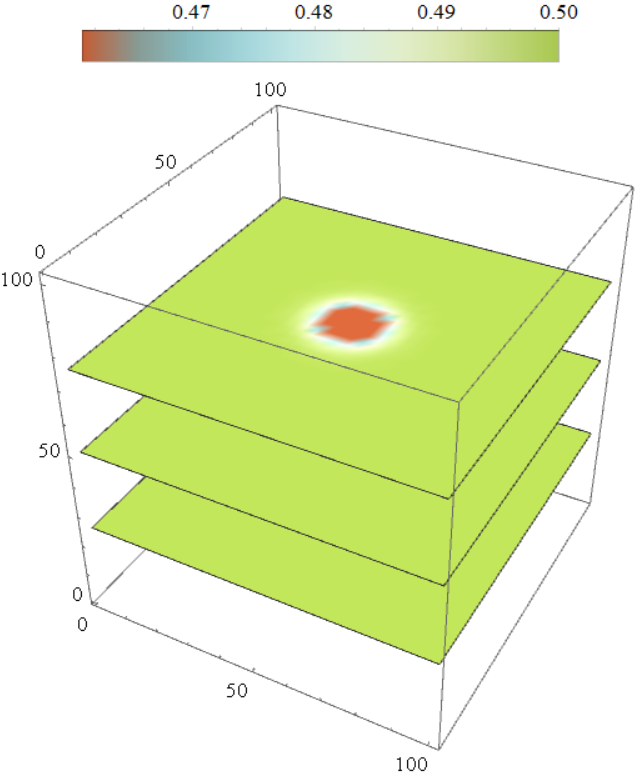
这里取$y=0$进行$x$方向进行Fourier变换，得到实空间中库伦势能

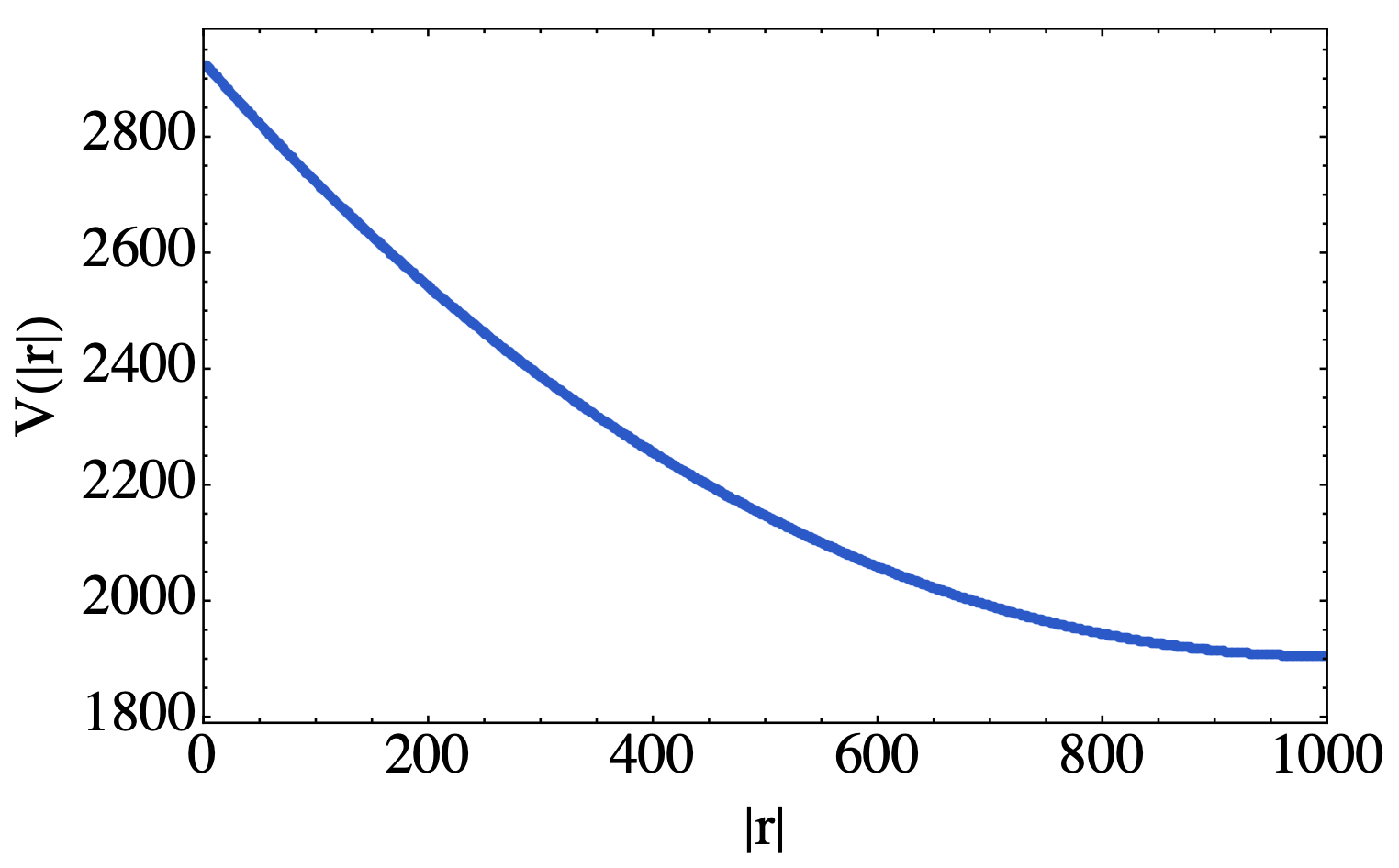
可以看到在$x$比较大的时候，排斥相互作用还是比较强的。

屏蔽库伦势

现在考虑屏蔽库伦势

$$V(\boldsymbol{k})=\frac{1}{\boldsymbol{k}}\tanh(\boldsymbol{k})$$

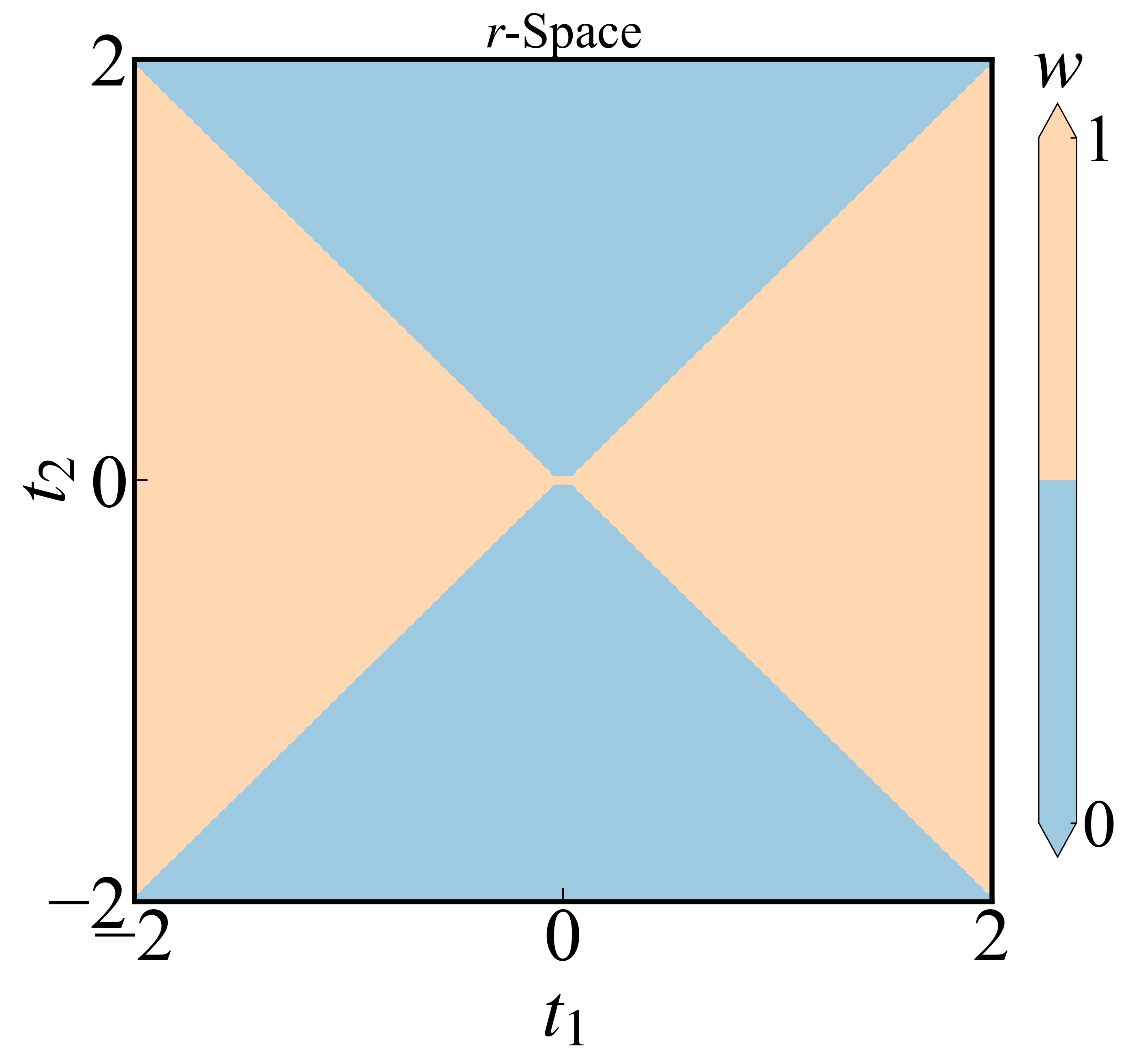
该势能在$\boldsymbol{k}\rightarrow 0$的时候并不是发散的，而是趋近于一个常数，其分布如下图所示

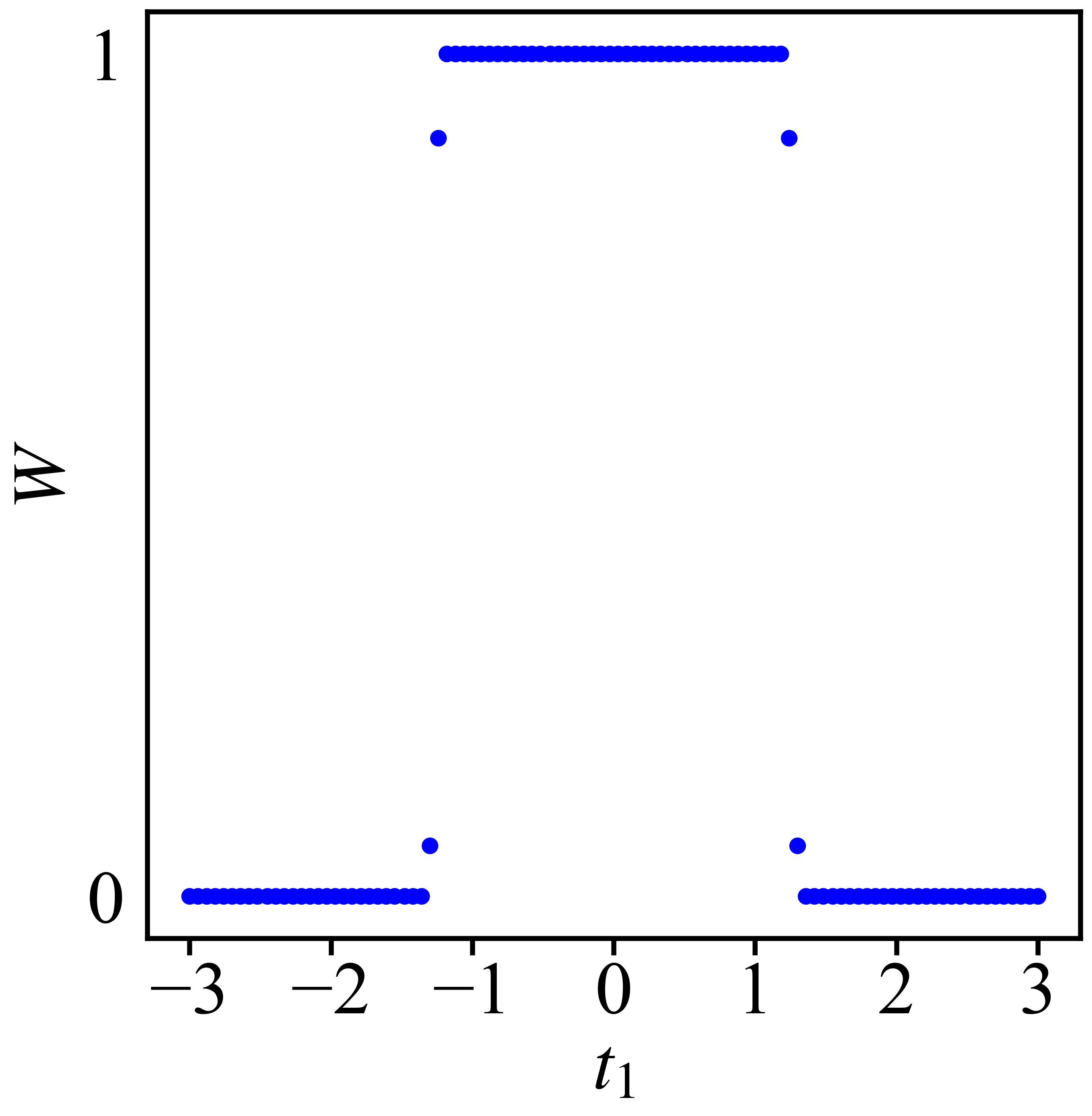
与前面的库伦势相同，对$x$方向做Fourier变换，并取$y=0$，可以得到

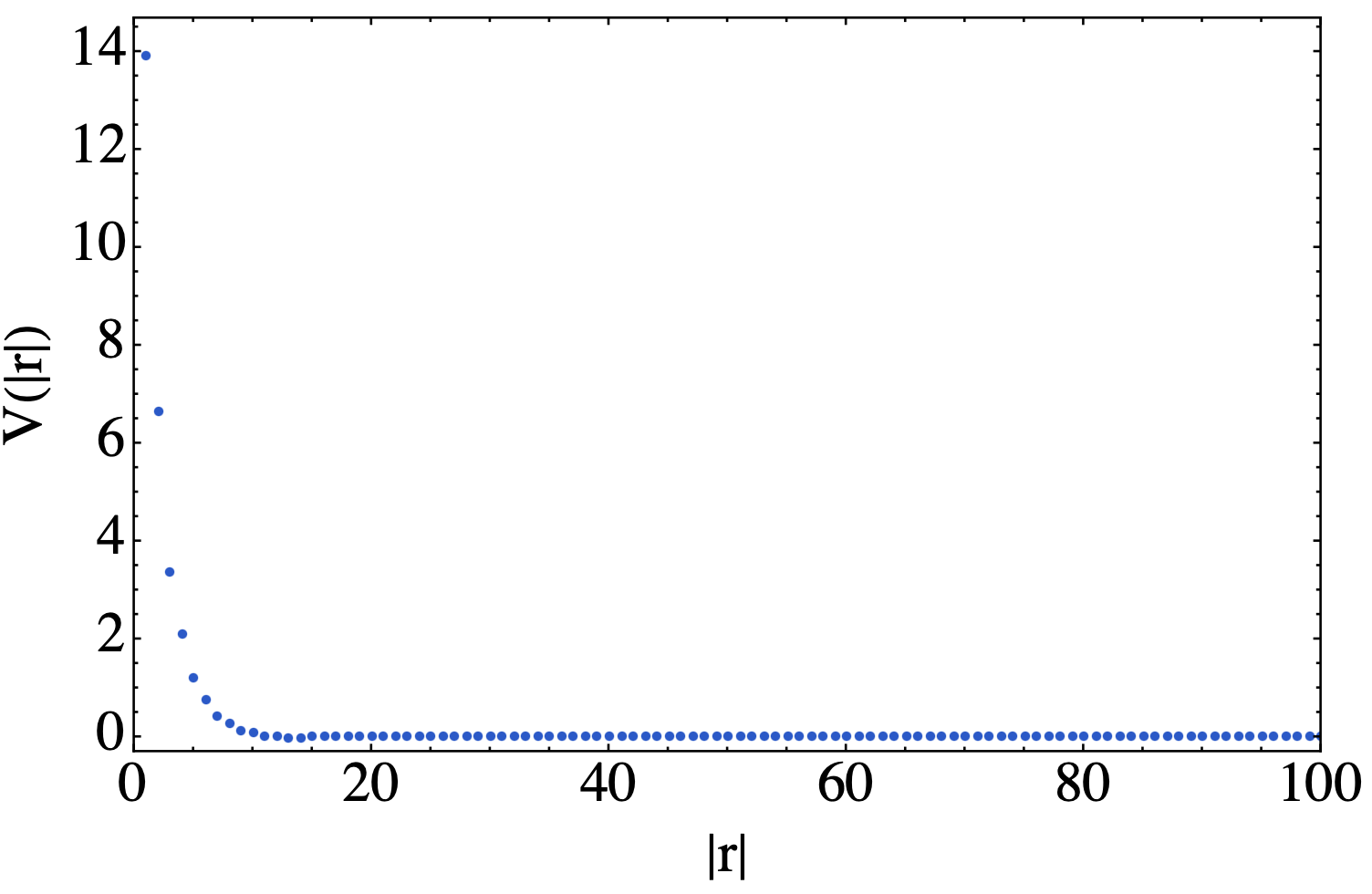
此时可以看到，屏蔽库伦势能在实空间会很快衰减。

代码

这里是用Mathematica做的快速Fourier变换，代码也贴一下

还有比较愚蠢的方式就是自己写程序进行上面的求和过程

@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Set_BZ(kn::Int64)
    knn::Int64 = 2 * kn + 1
    kmax::Float64 = pi
    klist = zeros(Float64,2,knn^2)
    ik0 = 0
    for ikx in -kn:kn
    for iky in -kn:kn
        ik0 += 1
        klist[1,ik0] = ikx * kmax/kn
        klist[2,ik0] = iky * kmax/kn
    end 
    end
    return  klist
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Bare_Coulomb_potential(qx::Float64,qy::Float64)
    re1::Float64 = 0.0
    dd0::Float64 = 40
    epsilon::Float64 = 4.0
    if (qx == 0 && qy == 0)
        # re1 = 2.0 * pi * dd0/epsilon
        re1 = 0.0
    else
        re1 = 2.0 * pi/(epsilon * sqrt(qx^2 + qy^2)) * tanh(dd0 * sqrt(qx^2 + qy^2))
    end
    return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Coulomb_Real(ix::Int64,iy::Int64)
    kn::Int64 = 1e2
    klist = Set_BZ(kn)
    re1::ComplexF64 =  0.0
    for ik0 in 1:(2 * kn + 1)^2
        kx, ky = klist[1,ik0],klist[2,ik0]
        re1 += Bare_Coulomb_potential(kx,ky) * exp(im * (kx * ix + ky * iy))
    end
    return real(re1)/(2 * kn + 1)^2
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function main1()
    xn::Int64 = 100
    re1 = SharedArray(zeros(Float64, xn, xn))
    @sync @distributed for ix in 1:xn
        for iy in 1:xn
            re1[ix,iy] = Coulomb_Real(ix,iy)
        end
    end
    fx1 = "Real_Coulobm.dat"
    f1 = open(fx1,"w")
    # x0 = (a->(@sprintf "%15.8f" a)).(re1)
    writedlm(f1,re1,"\t")
    close(f1)
end
#----------------------------------------------------------------------------------------------------------------------------
@time main1()

实际上用Julia也可以进行快速Fourier变换，这里就还是蠢办法上了。

参考

• 固体理论(李正中) p108

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
{:.info}

Email yxliphy@gmail.com