超导序参量中的傅里叶分析

整理一下在研究超导序参量的时候，理解傅里叶分析的一些笔记

最近在计算电子配对序参量，其中要分析序参量的配对对称性，这个时候可以采用Fourier变换，分解到不同的$\sin(n\theta)$和$\cos(n\theta)$通道中，通过比较哪个通道的系数最大，就可以确定序参量的位相在动量空间中的依赖关系。不过一般在费米面上绘制出序参量差不多也就可以看出对称性了。

$d_{x^2-y^2}$配对

首先是铜基超导中$d_{x^2-y^2}$电子配对，它的位相在动量空间的变换为

$$\Delta(\theta)=\cos(2\theta)$$

考虑将展开

$$\cos(2\theta)=\sum_{\omega_n}C(\omega)e^{i\omega_n\theta}$$

因为形式太简单了，所以可以手动进行Fourier展开

$$\cos(2\theta)=e^{i2\theta} + e^{-i2\theta}$$

因此可以知道在

$$\omega=2,\qquad \omega=-2$$

这两个频率处，Fourier展开系数$C(\omega)$会是最大的。

代码实现

下面就通过代码来演示一下上面的分析

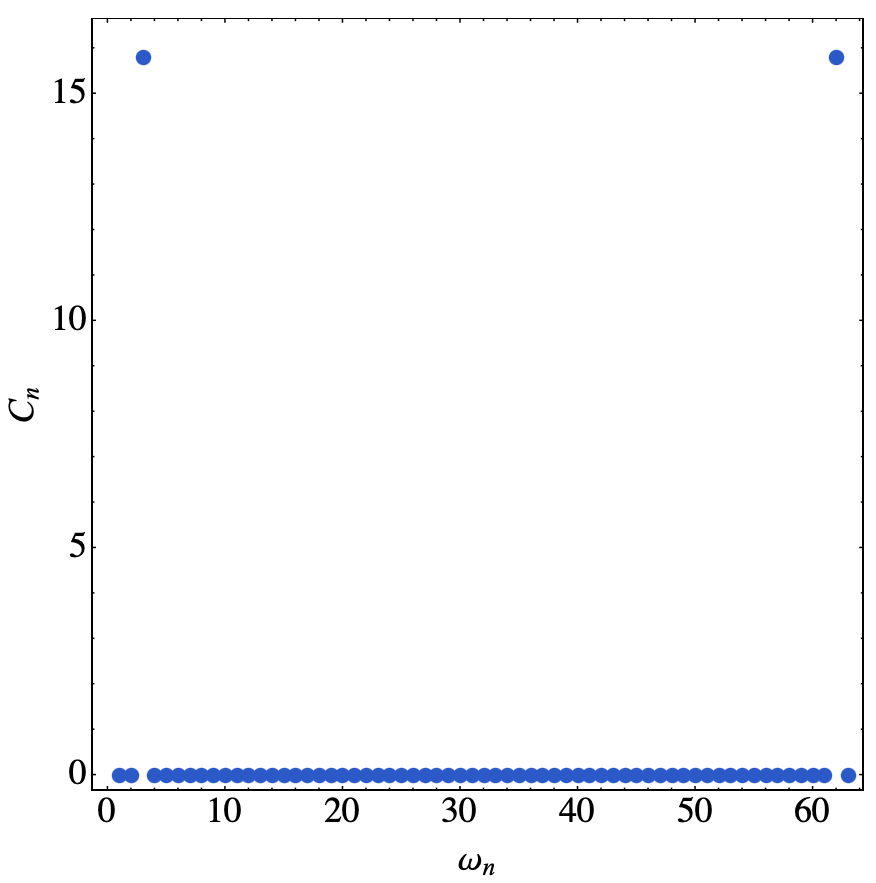
因为这里使用的是Mathematica的离散傅里叶变化，所以这里的$\omega_n$是会依赖于网格间距$dk$的，具体关于离散Fourier变化的算法自己不太懂，但使用这个方法的确是印证了上面的分析。

代码可以点击这里下载

参考文献

• Kohn-Luttinger Mechanism of Superconductivity in Twisted Bilayer WSe$_2$: Gate-Tunable Unconventional Pairing Symmetry
• Quantum Geometric Unconventional Superconductivity

鉴于该网站分享的大都是学习笔记，作者水平有限，若发现有问题可以发邮件给我

• yxliphy@gmail.com

也非常欢迎喜欢分享的小伙伴投稿