实验可测量与超导特征参数之间的关系(持续更新.......)

整理一下实验中如何测量超导一些特征参数。

超导相干长度与磁场关系

$2\pi\xi^2=\frac{\phi_0}{B_{c\perp}}，\quad \text{或者}\quad \xi=\left(\frac{\phi_0}{2\pi B_{c,\perp}}\right)^{\frac{1}{2}}$

其中$\phi_0$是超导量子磁通，$B_{c\perp}$是垂直方向的临界磁场。

正常态体系中电子的平均自由程$\ell$可以通过Drude电阻获得

$R\approx\frac{h}{e^2}\frac{1}{4k_F\ell}$

其中$h$是普朗克常熟，$k_F$是费米波矢。通过对比超导相干长度与电子平均自由程

$d=\frac{\xi}{\ell}$

这里的$d$是一个参数，如果$d<1$则被称为clean limit，表明体系是一个非常规超导体(unconventional superconductor)。从量子振荡中也可提取电子平均自由程

$\ell\approx2\pi k_F\ell^2_B$

其中$\ell_B$是磁长度

$\ell_B=\sqrt{\frac{\hbar}{eB}}$

$k_F$是费米波矢

$k_F=\sqrt{2\pi f_v|n_e|}$

png
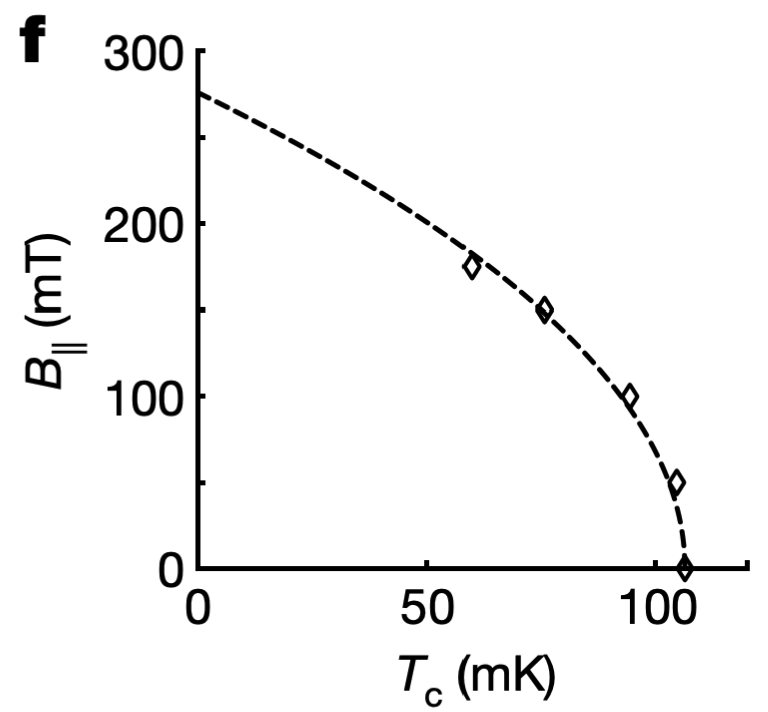
实验中在拟合超导相变温度随磁场变化曲线时使用的方程为

$\frac{T_C}{T_c^0}=1-\left(\frac{B_{c\parallel}}{B^0_{c\parallel}}\right)^2$

其中的$T_{c0}$是磁场$B_{\parallel}=0$时的超导转变温度，$B_{c\parallel}^0$则是$T=0$时的临界磁场，最终可以得到一个比例关系

$\frac{\mu_BB^0_{c\parallel}}{k_BT_c^0}=C_0$

这里的$C_0$是个常数，对于BCS弱耦合理论，这里的$C_0=1.23$。实验中通过$C_0$与BCS理论的预测值相比较来判断体系是处在弱耦合还是强耦合区间。

对于二维超导体而言，其面内临界磁场$B_{c\parallel}$相较于面外临界磁场$B_{c\perp}$要大一个量级，实验上通过对比两个不同方向的临界磁场来佐证体系是否具有二维超导电性的特征。

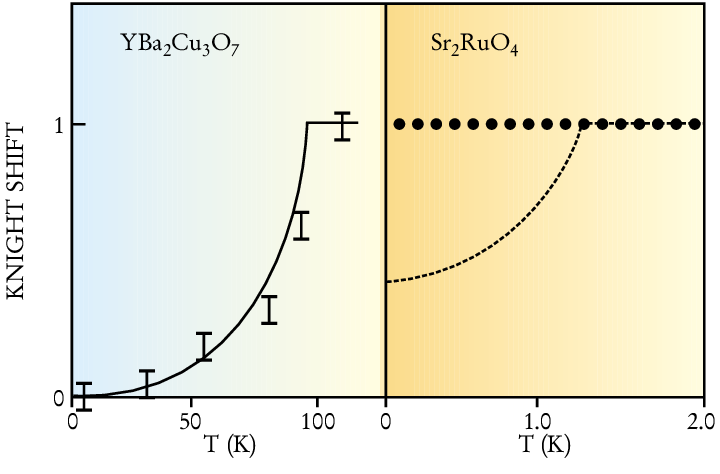
实验中施加平行磁场$B_{\parallel}$ ，通过输运测量电阻可以确定临界磁场$B_{c,\parallel}$。通过临界温度$T_c$可以得到Pauli极限在的临界磁场$B_{p}=T_c\times1.86 T/K$，而$B_p/B_{c,\parallel}$称为 Pauli-limit violation ratio(PIV)，如果这个比值小于$1$，说明体系的临界磁场是要大于Pauli极限的，通常可以认为电子配对可能是自旋三重态。

鉴于该网站分享的大都是学习笔记，作者水平有限，若发现有问题可以发邮件给我