当你计算某个量，发现需要在整个布里渊区撒很密的点，但计算量又受不了的时候，请抛弃老实人的做法，我们直接就是插值，获取定性结果即可。

起因

最近在重复文章，计算 RPA 修正库伦势

$V_{\boldsymbol{q}} = \frac{V_{0,\boldsymbol{q}}}{1 + \Pi_{0,\boldsymbol{q}} V_{0,\boldsymbol{q}}},$

其中

$\Pi_{0,\boldsymbol{q}} = N \sum_k |\Lambda_{\boldsymbol{k},\boldsymbol{q},\tau}|^2 \left\{ \frac{f(e_{\boldsymbol{k},\tau}) - f(e_{\boldsymbol{k}+\boldsymbol{q},\tau})}{e_{\boldsymbol{k}+\boldsymbol{q},\tau} - e_{\boldsymbol{k},\tau}} \right\}$

是静态极化函数$f(e)$ 是费米函数。如果要在整个布里渊区撒点，那么为了比较好的捕捉到势能的变化，此时网格密度就会比较高，计算量一下子就上来了。

那么有一个折中的方案:

现在一个稀疏的网格上计算出 $V(\boldsymbol{q})$

利用稀疏$V(\boldsymbol{q})$，通过数值的方式插值，来得到任意$(\boldsymbol{q})$处的屏蔽相互作用，然后再用插值得到的屏蔽势能来计算后续的结果

展示一下结果

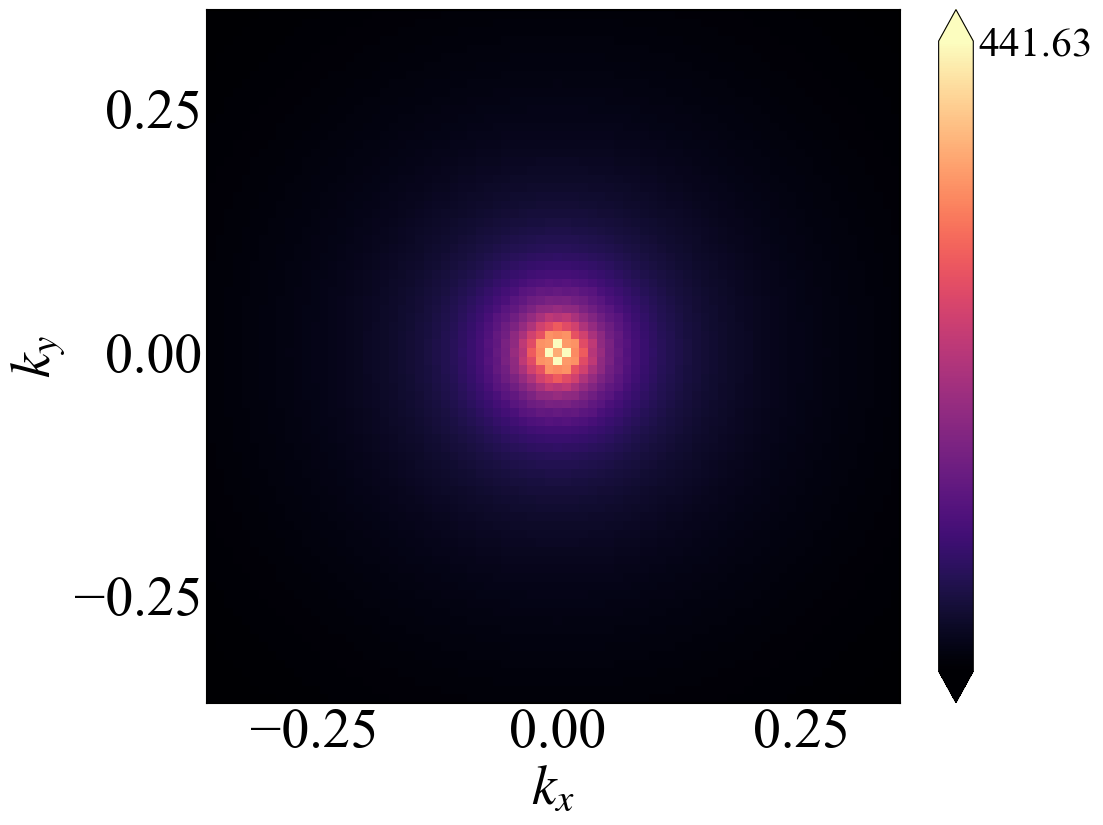
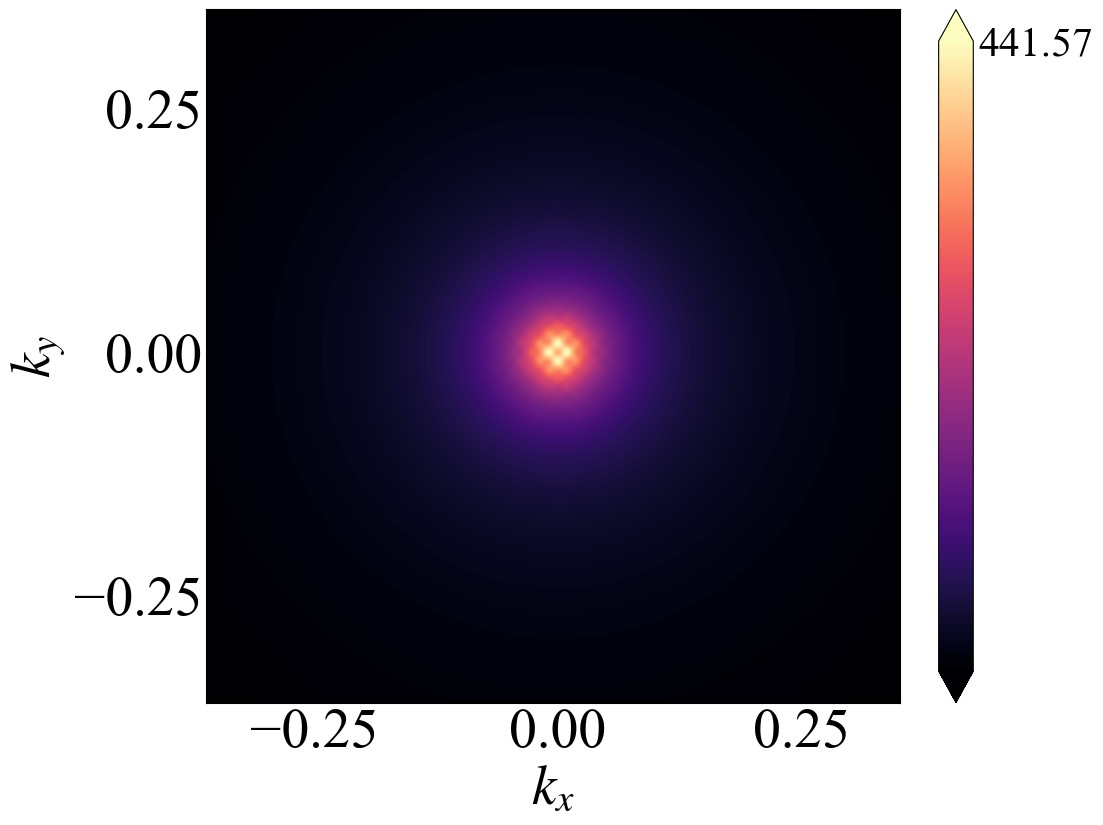
其中左图是在稀疏网格上直接计算的结果，右图就是进行插值，可以看到效果还是不错的。示例代码如下


function Charge_Susceptibility(qx::Float64, qy::Float64,
                               valmesh::Array{Float64, 3},
                               vecmesh::Array{ComplexF64, 4},
                               klist::Array{Float64, 3},
                               dk::Float64)
    hn = size(valmesh, 3)
    Nf = 4.0
    charge_Pi = 0.0 + 0.0im
    knx, kny = size(klist)[2], size(klist)[3]

    for ikx in 1:knx, iky in 1:kny
        kx, ky = klist[1, ikx, iky], klist[2, ikx, iky]
        for n in 1:hn
            Ek = valmesh[ikx, iky, n]
            psik = vecmesh[ikx, iky, :, n]
            Eq_all, psiq_all = eigen(matset(kx + qx, ky + qy))
            Eq = real(Eq_all[n])
            psiq = psiq_all[:, n]
            overlap = abs(psik' * psiq)^2
            denom = Eq - Ek
            re1 = abs(denom) > 1e-8 ? (fermi(Ek) - fermi(Eq)) / denom : -fermi_derivative(Ek)
            charge_Pi += overlap * re1
        end
    end
    return Nf * charge_Pi * dk^2 / (2pi)^2
end


function Vscr_interpolate_complex(
    Vscr_q::AbstractMatrix{ComplexF64},
    kn_old::Int,
    dk_old::Float64
)
    QN_old = 4 * kn_old
    q_old = ((1:QN_old) .- (2*kn_old + 1)) .* dk_old
    spl_re = Spline2D(q_old, q_old, real.(Vscr_q))
    spl_im = Spline2D(q_old, q_old, imag.(Vscr_q))
    qmin, qmax = first(q_old), last(q_old)
    return spl_re, spl_im, qmin, qmax  
end

第二个函数就会返回屏蔽相互作用样条插值的实部和虚部，后面使用就可以直接调用来得到任意位置上的屏蔽势能了。给个计算超导序参量的结果图对比

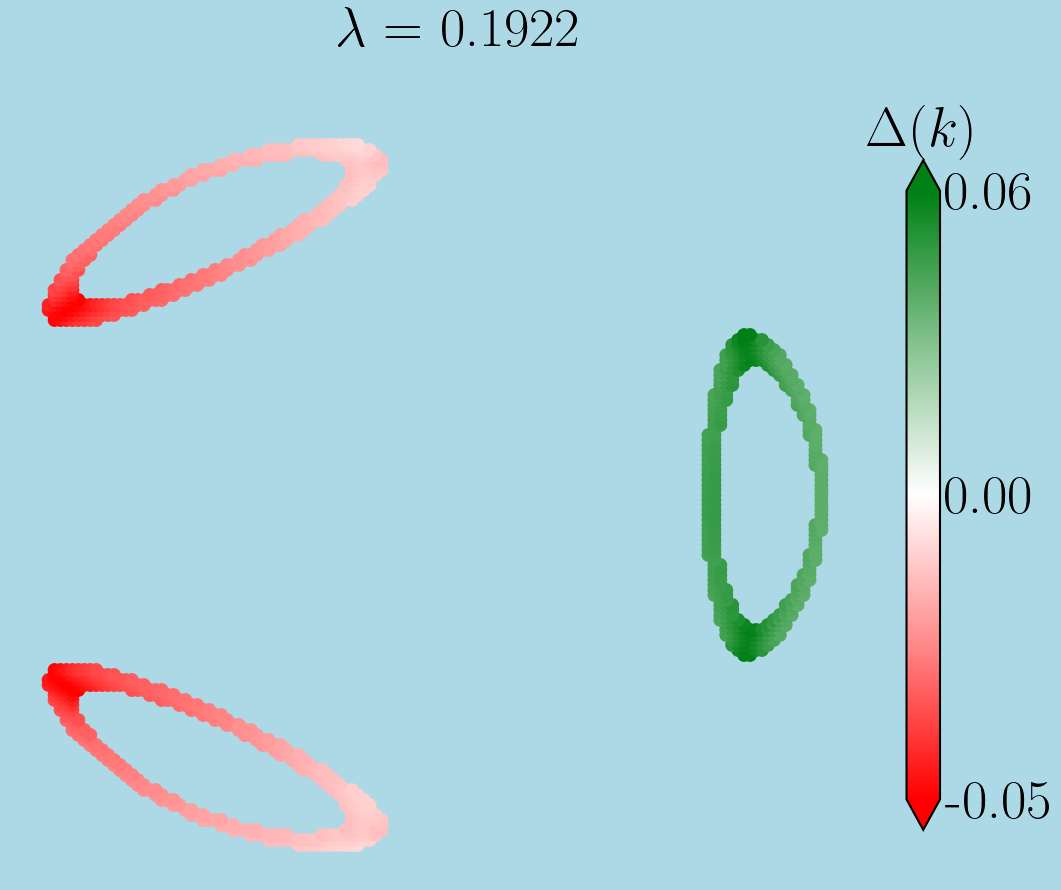
左图是直接计算得到的结果，右图则是在一个很稀疏的网格上先计算屏蔽势，然后在很密的网格上插值，同时计算稠密网格上的费米点并计算出配对序参量。从结果来看，如果只是关心定性结果的话，插值方法是可以接受的。而且利用插值方法对于计算时间的节省是很显著的，直接计算需要$N_x\times N_y=256*256$，上述计算在插值的时候$N_x\times N_y=20\times 20$。把这个数量再代入到 RPA 修正部分，速度提升是非常可观的。所以在测试一些课题的时候，可以先插值定性，等问题分析清楚，再直接计算来得到精确的结果。