轨道磁矩推导笔记

轨道磁矩推导

在量子力学中，轨道角动量的定义是 $\mathbf{L} = \mathbf{r} \times \mathbf{p}$。但在无限大的周期性晶体中，电子是弥散在整个空间的（布洛赫波），位置算符 $\mathbf{r}$ 在这个基底下是没有良好定义的（因为它不符合周期性边界条件）。既然 $\mathbf{r}$ 定义不清楚，那么基于 $\mathbf{r}$ 的轨道角动量 $\mathbf{L}$，以及由此产生的轨道磁矩也随之变得“ill-defined”（定义不明确）。

将 $n$ 能带的波包定义为

$|W_n\rangle = \int d\mathbf{k} w(\mathbf{k}) |\psi_{n\mathbf{k}}\rangle$

其中 $|\psi_{n\mathbf{k}}\rangle = e^{i\mathbf{k}\cdot\mathbf{r}}|u_{n\mathbf{k}}\rangle$ 是布洛赫态。为了方便推导，取窄波包近似，即 $|w(\mathbf{k})|^2 \approx \delta(\mathbf{k} - \mathbf{k}_c)$。轨道磁矩的物理定义源于电流环路对空间的贡献，其半经典表达式为

$\mathbf{m}_n^O = -\frac{e}{2} \langle W_n | (\mathbf{r} - \mathbf{r}_c) \times \mathbf{\dot{r}} | W_n \rangle$

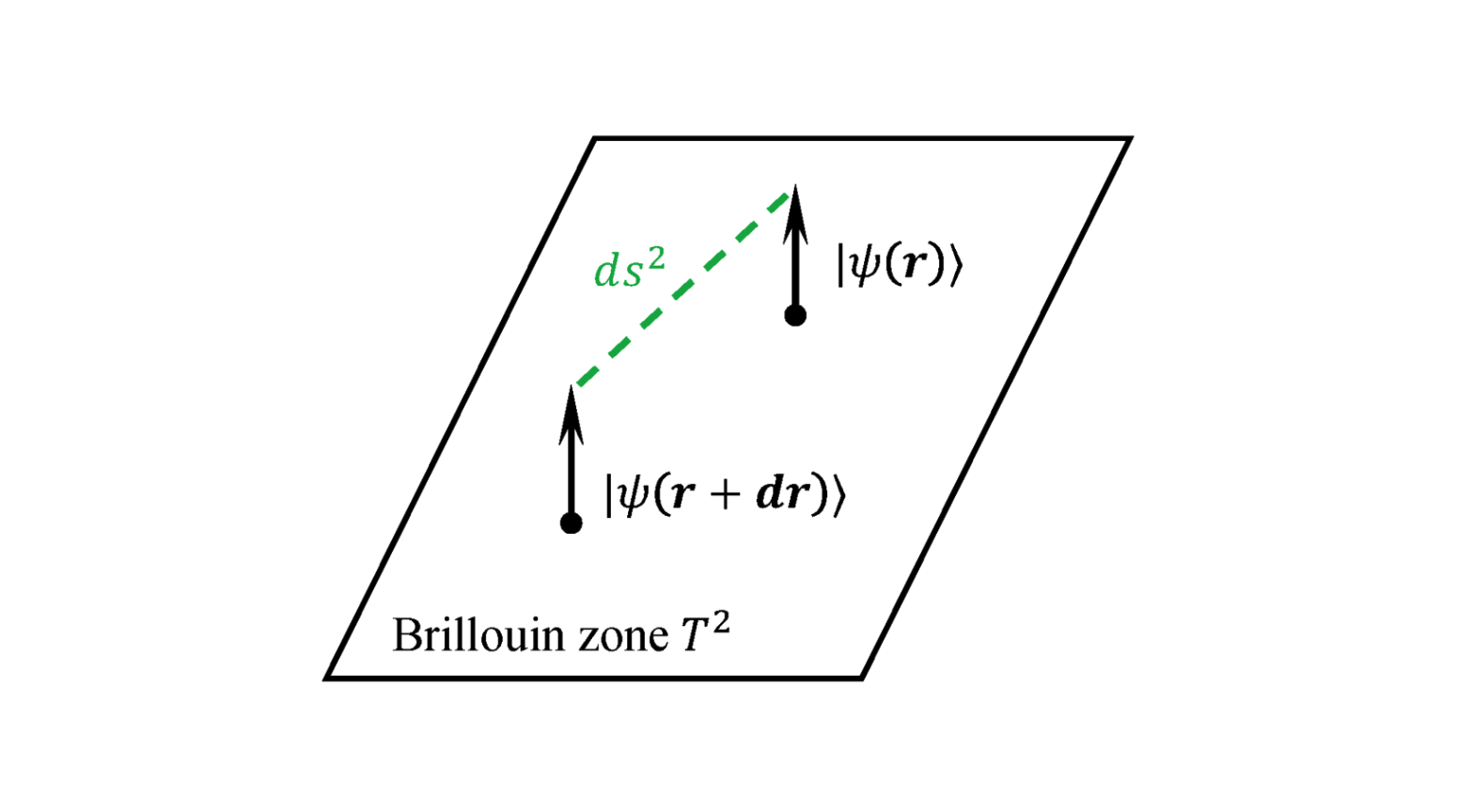
其中 $\mathbf{r}_c = \langle W_n | \mathbf{r} | W_n \rangle$ 是波包的几何中心。在布洛赫基底下，位置算符 $\mathbf{r}$ 的作用不能直接写成 $\mathbf{r}$，因为它破坏了平移对称性。通过对布洛赫波函数求梯度，可以得到

$\mathbf{r} |\psi_{n\mathbf{k}}\rangle = e^{i\mathbf{k}\cdot\mathbf{r}} (i \partial_\mathbf{k} + \mathbf{r}) |u_{n\mathbf{k}}\rangle \Rightarrow (i \partial_\mathbf{k} + \mathcal{A}_n) |u_{n\mathbf{k}}\rangle$

其中 $\mathcal{A}_n = i\langle u_{n\mathbf{k}} | \partial_\mathbf{k} u_{n\mathbf{k}} \rangle$ 是 Berry 联络（Berry Connection）。同理，速度算符 $\mathbf{\dot{r}}$ 由海森堡方程给出

$\mathbf{\dot{r}} = \frac{1}{i\hbar} [\mathbf{r}, \mathcal{H}]$

在波包中心 $\mathbf{k}_c$ 处，其对角项对应群速度 $v_n = \frac{1}{\hbar} \partial_\mathbf{k} \varepsilon_n$，但磁矩涉及到的是相对位置和相对速度的乘积。将算符 $(\mathbf{r} - \mathbf{r}_c) \times \mathbf{\dot{r}}$ 插入到波包状态中。由于波包是非常窄的，可以将积分转为对 $\mathbf{k}$ 空间单一能带的求和。插入完备性关系 $\sum_m |m\rangle\langle m| = 1$

$\mathbf{m}_n^O = -\frac{e}{2} \sum_{m \neq n} \langle n | (\mathbf{r} - \mathbf{r}_c) | m \rangle \times \langle m | \mathbf{\dot{r}} | n \rangle\label{eq:q1}$

当 $m=n$ 时，$(\mathbf{r}-\mathbf{r}_c)$ 的期望值为零，因此贡献全部来自于带间跃迁（Inter-band transitions）。利用矩阵元的恒等式

$\begin{aligned} &\langle n | \mathbf{r} | m \rangle = i\langle u_n | \partial_\mathbf{k} u_m \rangle （ m \neq n）\\ &\langle m | \mathbf{\dot{r}} | n \rangle = \frac{1}{i\hbar} (\varepsilon_n - \varepsilon_m) \langle u_m | \mathbf{r} | u_n \rangle \end{aligned}$

将上述矩阵元代回磁矩表达式$\eqref{eq:q1}$中

$\mathbf{m}_n^O = -\frac{e}{2\hbar} \text{Im} \sum_{m \neq n} \langle \psi_n | \mathbf{r} | \psi_m \rangle \times \langle \psi_m | [ \mathbf{r}, \mathcal{H} ] | \psi_n \rangle$

为了处理坐标算符 $\mathbf{r}$，我们利用布洛赫波函数的特性。对于 $m \neq n$，位置算符的矩阵元可以转化为偏导数形式

$\langle \psi_n | \mathbf{r} | \psi_m \rangle = i \langle n | \partial_\mathbf{k} m \rangle$

同时，利用薛定谔方程 $\mathcal{H}|m\rangle = \varepsilon_m |m\rangle$，速度算符的矩阵元可以写为

$\langle m | [\mathbf{r}, \mathcal{H}] | n \rangle = (\varepsilon_n - \varepsilon_m) \langle m | \mathbf{r} | n \rangle = (\varepsilon_n - \varepsilon_m) i \langle m | \partial_\mathbf{k} n \rangle$

将这两者代入磁矩公式，得到

$\mathbf{m}_n^O = -\frac{e}{2\hbar} \text{Im} \sum_{m \neq n} (\varepsilon_n - \varepsilon_m) \langle \partial_\mathbf{k} n | m \rangle \times \langle m | \partial_\mathbf{k} n \rangle\label{eq:q2}$

注意到 $(\varepsilon_n - \varepsilon_m)$ 项可以被看作是算符 $(\varepsilon_n - \mathcal{H})$ 作用在状态 $|m\rangle$ 上的结果。由于 $\sum_{m} |m\rangle \langle m| = 1$，可以尝试展开求和项

$\sum_{m \neq n} (\varepsilon_n - \varepsilon_m) | m \rangle \langle m | = (\varepsilon_n - \mathcal{H}) \sum_{m \neq n} | m \rangle \langle m |$

因为对于 $m=n$ 的项，$(\varepsilon_n - \mathcal{H})|n\rangle = 0$，可以将求和范围扩大到包含 $n$ 在内的所有能带

$(\varepsilon_n - \mathcal{H}) \sum_{all \ m} | m \rangle \langle m | = (\varepsilon_n - \mathcal{H}) \cdot \mathbf{1}$

代入方程$\eqref{eq:q2}$中得到

$\mathbf{m}_n^O = -\frac{e}{2\hbar} \text{Im} \langle \partial_\mathbf{k} n | \times (\varepsilon_n - \mathcal{H}) \left( \sum_{m} | m \rangle \langle m | \right) | \partial_\mathbf{k} n \rangle$

利用完备性关系 $\sum |m\rangle\langle m| = 1$，中间的求和项消失，从而得到

$\mathbf{m}_n^O = -\frac{e}{2\hbar} \text{Im} \langle \partial_\mathbf{k} n | \times (\varepsilon_n - \mathcal{H}) | \partial_\mathbf{k} n \rangle= \frac{e}{2\hbar} \text{Im} \langle \partial_\mathbf{k} n | \times (\mathcal{H}-\varepsilon_n) | \partial_\mathbf{k} n \rangle$

能带态 $|n\rangle$ 的导数与其它能带 $|m\rangle$ 之间存在如下关系

$\langle m | \partial_i n \rangle = \frac{\langle m | \partial_i \mathcal{H} | n \rangle}{\varepsilon_n - \varepsilon_m} \quad (m \neq n)\label{eq:q3}$

利用完备性关系，得到

$\langle \partial_i n | (\mathcal{H} - \varepsilon_n) \left( \sum_m |m\rangle \langle m| \right) | \partial_j n \rangle = \sum_m (\varepsilon_m - \varepsilon_n) \langle \partial_i n | m \rangle \langle m | \partial_j n \rangle$

当 $m=n$ 时，$(\varepsilon_n - \varepsilon_n) = 0$，因此求和自动限制在 $m \neq n$。利用公式$\eqref{eq:q3}$得到

$\sum_{m \neq n} (\varepsilon_m - \varepsilon_n) \left( \frac{\langle n | \partial_i \mathcal{H} | m \rangle}{\varepsilon_n - \varepsilon_m} \right) \left( \frac{\langle m | \partial_j \mathcal{H} | n \rangle}{\varepsilon_n - \varepsilon_m} \right)$

化简系数项

$\frac{\varepsilon_m - \varepsilon_n}{(\varepsilon_n - \varepsilon_m)^2} = \frac{-(\varepsilon_n - \varepsilon_m)}{(\varepsilon_n - \varepsilon_m)^2} = -\frac{1}{\varepsilon_n - \varepsilon_m}$

最终得到

$m_n^{\text{O}, ij} = \frac{e}{2\hbar} \text{Im} \left[ -\sum_{m \neq n} \frac{\langle n | \partial_i \mathcal{H} | m \rangle \langle m | \partial_j \mathcal{H} | n \rangle}{\varepsilon_n - \varepsilon_m} \right]$