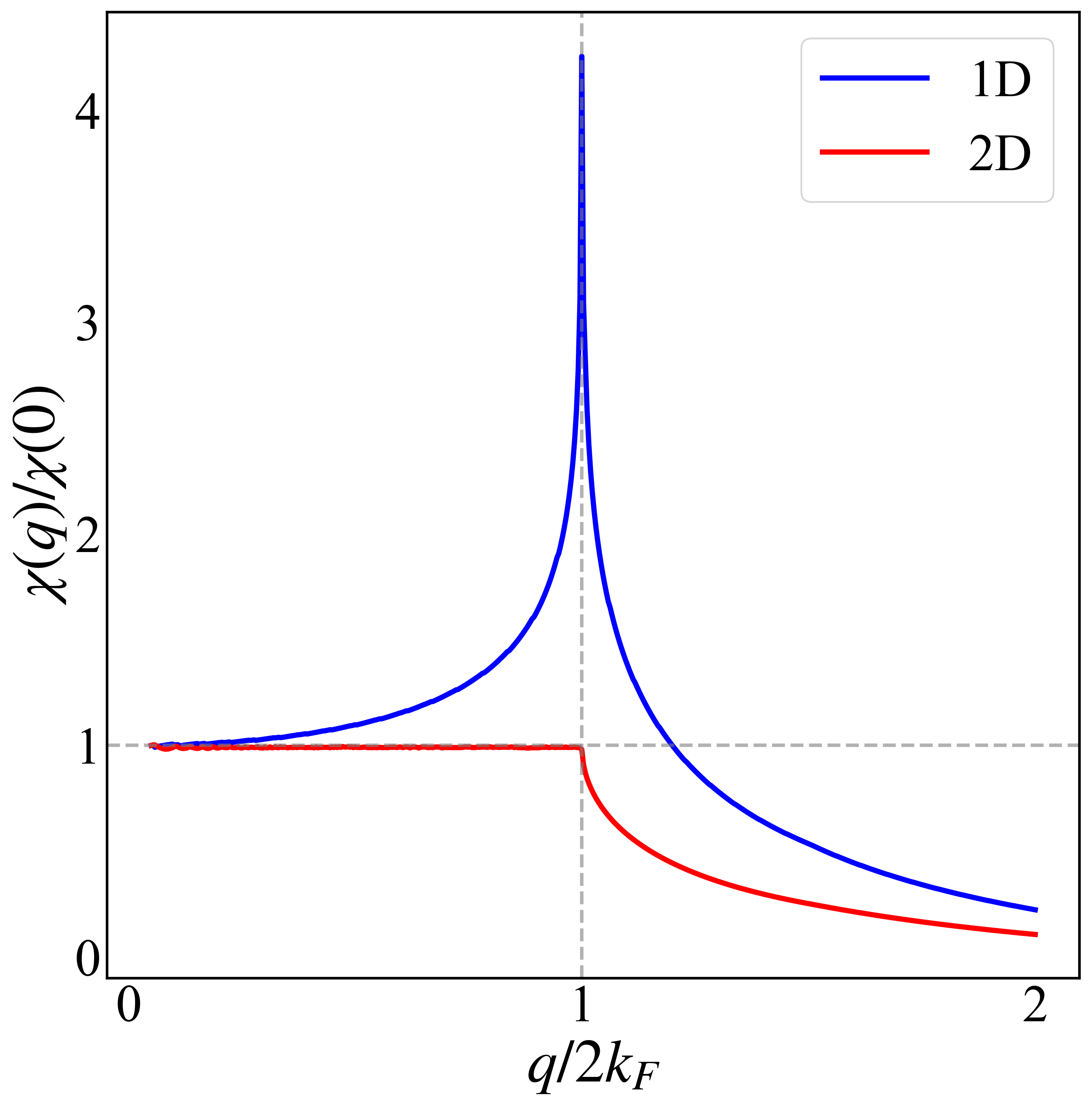
一维与二维体系的静态极化率(数值计算)

极化率计算公式为

$\Pi(q) = \frac{1}{N} \sum_{k} \frac{f(\epsilon_k) - f(\epsilon_{k+q})}{\epsilon_k - \epsilon_{k+q} + i\eta}$

这里对一维和二维自由电子模型计算极化率，使用连续模型进行计算，目的是为了方便与解析上的分析对应。

$\begin{aligned} &1D:\qquad \epsilon(k) = -2t \cos(k)\\ &2D:\qquad \epsilon(k_x, k_y) = -2t (\cos(k_x) + \cos(k_y)) \end{aligned}$

计算程序

using Distributed

# 初始化并行环境（根据 CPU 核心数添加进程）
if nworkers() == 1
    addprocs() 
end

@everywhere begin
    using LinearAlgebra
    using Printf

    const m = 1.0
    const hbar = 1.0
    const kF = 1.0
    const EF = (hbar^2 * kF^2) / (2 * m)
    const T = 1e-8         
    const eta = 1e-3       
    const g_s = 2.0         

    epsilon(k_vec) = (hbar^2 * sum(k_vec.^2)) / (2 * m)
    function fermi(e)
        x = (e - EF) / T
        return 0.5 * (1.0 - tanh(0.5 * x))
    end

    # 1D 计算函数
    function compute_pi_1d(q_val; Nk=3000)
        k_max = 4.0 * kF
        k_grid = range(-k_max, k_max, length=Nk)
        dk = k_grid[2] - k_grid[1]
        res = 0.0 + 0.0im
        for k in k_grid
            ek = epsilon([k])
            ekq = epsilon([k + q_val])
            res += (fermi(ek) - fermi(ekq)) / (ek - ekq + 1im * eta)
        end
        return real(res * (g_s / (2π)) * dk)
    end

    # 2D 计算函数
    function compute_pi_2d(q_val; Nk=2000)
        k_max = 4.0 * kF
        k_vals = range(-k_max, k_max, length=Nk)
        dk2 = (k_vals[2] - k_vals[1])^2
        res = 0.0 + 0.0im
        q_vec = [q_val, 0.0]
        for kx in k_vals, ky in k_vals
            k_vec = [kx, ky]
            kq_vec = k_vec .+ q_vec
            ek = epsilon(k_vec)
            ekq = epsilon(kq_vec)
            res += (fermi(ek) - fermi(ekq)) / (ek - ekq + 1im * eta)
        end
        return real(res * (g_s / (2π)^2) * dk2)
    end

    # 为了 pmap 方便，封装一个同时返回 1D 和 2D 的包装函数
    function compute_all_pi(q)
        return (compute_pi_1d(q), compute_pi_2d(q))
    end
end
q_range = range(0.1, 4.0 * kF, length=500)

println("正在使用 $(nworkers()) 个进程并行计算...")
results = pmap(compute_all_pi, q_range)

# 归一化数据
pi_1d_raw = [r[1] for r in results]
pi_2d_raw = [r[2] for r in results]

pi0_1d = pi_1d_raw[1]
pi0_2d = pi_2d_raw[1]


filename = "lindhard_continuous.dat"
open(filename, "w") do io
    write(io, "# q \t\t Pi_1D_norm \t Pi_2D_norm \n")
    for i in 1:length(q_range)
        p1_norm = pi_1d_raw[i] / pi0_1d
        p2_norm = pi_2d_raw[i] / pi0_2d
        @printf(io, "%.6f \t %.10f \t %.10f \n", q_range[i], p1_norm, p2_norm)
    end
end

绘图程序

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os

# 1. Latex 字体与全局样式设置
plt.rc('font', family='Times New Roman')
config = {
    "font.size": 22,
    "mathtext.fontset": 'stix',
    "axes.unicode_minus": False 
}
rcParams.update(config)
#------------------------------------------------------------------------------------
def plot_polarization(dat_file):
    """
    整合 plotfs 风格与极化率特有的图例、辅助线标记
    """
    if not os.path.exists(dat_file):
        print(f"Error: File '{dat_file}' not found.")
        return

    # 1. 加载数据
    data = np.loadtxt(dat_file)
    x0 = data[:, 0] / 2.0  # 归一化 q/2kF
    pi_1d = data[:, 1]
    pi_2d = data[:, 2]
    
    # 2. 创建画布 (参照 plotfs 10x10 比例)
    plt.figure(figsize=(10, 10))
    
    # 3. 绘图：保留颜色对比与图例标签
    plt.plot(x0, pi_1d, lw=3, c="b", label="1D")
    plt.plot(x0, pi_2d, lw=3, c="r", label="2D")

    # 4. 保留物理标记：q=2kF (即 x=1.0) 的辅助虚线
    plt.axvline(x=1.0, color='gray', linestyle='--', lw=2, alpha=0.6)

    # 5. 字体与字号设置 (参照 plotfs)
    font2 = {'family': 'Times New Roman',
             'weight': 'normal',
             'size': 35,
             }

    plt.xlabel(r"$q/2k_F$", font2)
    plt.ylabel(r"$\chi(q)/\chi(0)$", font2)

    # 6. 保留图例 (参照 plotfs 注释掉的 legend 逻辑并启用)
    # 使用 markerscale=2 保证图例线段足够明显
    plt.legend(loc='best',  prop={'family': 'Times New Roman', 'size': 30})

    # 7. 刻度参数设置 (完全参照 plotfs)
    plt.tick_params(direction='in', axis='x', width=0, length=10, labelsize=30)
    plt.tick_params(direction='in', axis='y', width=0, length=10, labelsize=30)

    # 8. 边框加粗 (完全参照 plotfs)
    ax = plt.gca()
    ax.spines["bottom"].set_linewidth(1.5)
    ax.spines["left"].set_linewidth(1.5) 
    ax.spines["right"].set_linewidth(1.5)
    ax.spines["top"].set_linewidth(1.5)

    # 9. 限制坐标刻度数量 (这是你要求的关键修改方式)
    ax.locator_params(axis='x', nbins=3)
    ax.locator_params(axis='y', nbins=5)
    # 3. 辅助线
    ax.axhline(y=1.0, color='gray', linestyle='--', linewidth=2, alpha=0.6)

    # 10. 保存
    picname = os.path.splitext(dat_file)[0] + ".png"
    plt.savefig(picname, dpi=300, bbox_inches='tight')
    plt.close()
#---------------------------------------------------------------------
if __name__ == "__main__":
    plot_polarization("lindhard_continuous.dat")