超导中的Fulde-Ferrell 态与Larkin-Ovchinnikov态

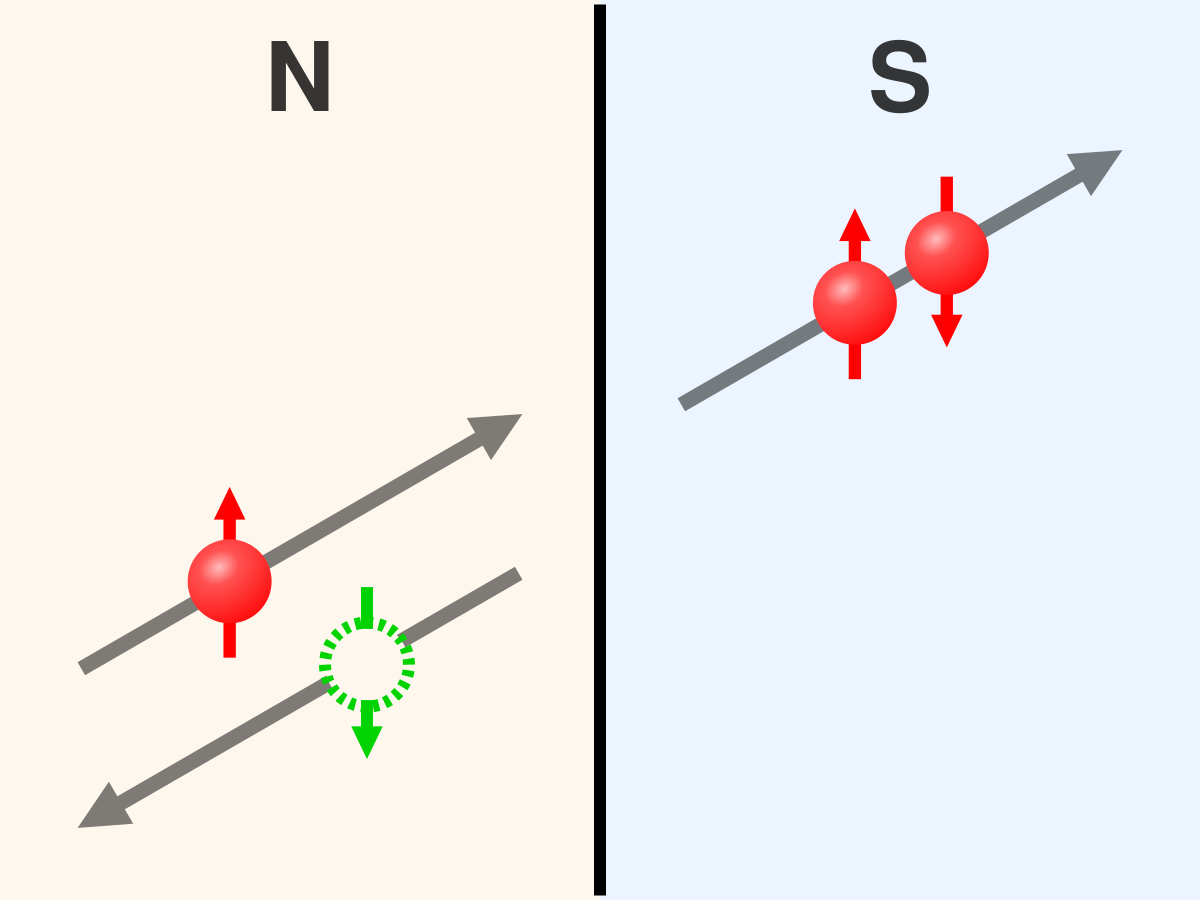
通常超导态中的库珀对是由动量相反的电子（$k, \uparrow$）和（$-k, \downarrow$）组成的，总动量为零。但在强磁场下，自旋向上和向下的费米面发生移动（塞曼分裂），为了让库珀对继续存在，电子会形成具有有限中心质量动量 $q$ 的对。

FF态 (Fulde-Ferrell)

FF态由 Fulde 和 Ferrell 提出，其超导序参数在空间上表现为单平面波形式

$\Delta(\mathbf{r}) = \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}}$

序参数的振幅 $|\Delta(\mathbf{r})|$ 在空间中是常数，但其相位随空间位置线性变化。由于存在单向的动量 $\mathbf{q}$，该状态具有超导电流，打破了时间反演对称性。

LO态 (Larkin-Ovchinnikov)

LO态由 Larkin 和 Ovchinnikov 提出，其序参数是两个相反动量的平面波的叠加，形成驻波形式

$\Delta(\mathbf{r}) = \Delta_0 \cos(\mathbf{q} \cdot \mathbf{r}) \quad \text{或} \quad \Delta_0 \sin(\mathbf{q} \cdot \mathbf{r})$

序参数的振幅在空间中呈现周期性震荡，并且会改变符号。在 $\Delta(\mathbf{r}) = 0$ 的地方（节点），超导电性消失，这些区域实际上变成了正磁化的正常态金属区。由于是 $+q$ 和 $-q$ 的等量叠加，所以LO态宏观上不产生净电流。

Ginzburg-Landau (GL) 理论分析

通过对自由能的分析，可以对上述两种有限动量配对态的能量进行分析。在常规超导体中，自由能对梯度算子的展开通常只到二阶 $|\nabla \psi|^2$。但在 FFLO 态出现的临界点（Lifshitz 点）附近，由于磁场导致动量不为零，二阶项系数 $K_1$ 会变号。为了保证稳定性，必须引入更高级的项。自由能密度 $f$ 可以展开为

$f = \alpha |\psi|^2 + K_1 |\nabla \psi|^2 + K_2 |\nabla^2 \psi|^2 + \frac{\beta}{2} |\psi|^4\label{eq:f1}$

当 $K_1 < 0$ 时，均匀超导态（$\nabla \psi = 0$）不再稳定，系统倾向于通过非零梯度（即动量 $q$）来降低能量。假定序参数具有单平面波的形式$\psi(\mathbf{r}) = \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}}$，其中 $\Delta_0$ 是振幅，$q$ 是我们要确定的调制动量。将 $\psi(\mathbf{r})$ 代入自由能密度的表达式$\eqref{eq:f1}$中

$\begin{aligned} &\nabla \psi = i\mathbf{q} \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}}\Rightarrow |\nabla \psi|^2 = (\nabla \psi) \cdot (\nabla \psi)^* = q^2 \Delta_0^2\\ &\nabla^2 \psi = \nabla \cdot (i\mathbf{q} \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}}) = (i\mathbf{q}) \cdot (i\mathbf{q}) \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}} = -q^2 \psi\Rightarrow |\nabla^2 \psi|^2 = (-q^2 \Delta_0 e^{i\mathbf{q} \cdot \mathbf{r}}) \cdot (-q^2 \Delta_0 e^{-i\mathbf{q} \cdot \mathbf{r}}) = q^4 \Delta_0^2 \end{aligned}$

得到自由能密度为

$\begin{aligned} f(q) &= \alpha \Delta_0^2 + K_1 (q^2 \Delta_0^2) + K_2 (q^4 \Delta_0^2) + \frac{\beta}{2} \Delta_0^4\\ &= (\alpha + K_1 q^2 + K_2 q^4) \Delta_0^2 + \frac{\beta}{2} \Delta_0^4 \end{aligned}$

为了找到使能量最低的调制波矢，我们需要对 $q^2$ 求导并令其等于零（极值条件）

$\frac{\partial f}{\partial (q^2)} = (K_1 + 2 K_2 q^2) \Delta_0^2 = 0$

假设超导态已形成（$\Delta_0 \neq 0$），则必须满足

$K_1 + 2 K_2 q^2 = 0$

从而得到

$q^2 = -\frac{K_1}{2 K_2} \Rightarrow q_0 = \sqrt{\frac{-K_1}{2 K_2}}$

存在条件：由于 $q^2$ 必须为正，因此该公式直接要求 $K_1 < 0$。在常规超导体中 $K_1 > 0$，此时 $q=0$（均匀态）能量最低。只有当磁场或自旋不平衡导致 $K_1$ 变号时，系统才会自发选择一个有限的 $q_0$。

稳定性：为了防止能量随 $q$ 无限增加而发散，必须要求 $K_2 > 0$。这确保了自由能曲线是一个开口向上的“双阱”形或具有明确的极小值点。

FF态

接下来比较两种态的能量，对于FF态$\psi_{FF}(\mathbf{r}) = \Delta_0 e^{i\mathbf{q}\cdot\mathbf{r}}$，其自由能为

$\langle f \rangle_{FF} = (\alpha + K_1 q^2 + K_2 q^4) \Delta_0^2 + \frac{\beta}{2} \Delta_0^4$

令系数 $A(q) = \alpha + K_1 q^2 + K_2 q^4$，极小化 $\Delta_0$ 得到 $\Delta_0^2 = -A(q)/\beta$，则

$\langle f \rangle_{FF} = -\frac{A(q)^2}{2\beta}$

LO态

对于LO态$\psi_{LO}(\mathbf{r}) = \sqrt{2} \Delta_0 \cos(\mathbf{q}\cdot\mathbf{r})$(这里 $\sqrt{2}$ 是为了归一化平均振幅，便于比较)，梯度项与FF态相同，而四次项则不同

$\langle |\psi|^4 \rangle = \langle 4 \Delta_0^4 \cos^4(\mathbf{q}\cdot\mathbf{r}) \rangle = 4 \Delta_0^4 \cdot \frac{3}{8} = \frac{3}{2} \Delta_0^4$

平面波的 $\langle |e^{iqr}|^4 \rangle = 1$，而余弦波的 $\langle |\cos(qr)|^4 \rangle$ 会多出一个系数 $3/2$。因此LO态的平均自由能为

$\langle f \rangle_{LO} = A(q) \Delta_0^2 + \frac{3\beta}{4} \Delta_0^4$

极小化 $\Delta_0$ 得到 $\Delta_0^2 = -2A(q)/3\beta$，代回得

$\langle f \rangle_{LO} = -\frac{A(q)^2}{3\beta}$

综上可得

$\langle f \rangle_{LO} = -\frac{A(q)^2}{1.5\beta} \quad \text{vs} \quad \langle f \rangle_{FF} = -\frac{A(q)^2}{2\beta}$

可以看到通常LO态的能量更低，LO态通过在空间中形成节点，能够更有效地协调磁场产生的去配对效应。在节点处，超导序参数为零，这允许系统在这些区域容纳磁场产生的准粒子激发的能量。LO 态通过空间调制，虽然在四次方项上看起来“吃亏”（系数大），但在强磁场环境下，它允许在节点（Node）位置完全释放顺磁能量。因此，通过简单的分析，在 GL 理论范围内，LO 态的自由能通常低于 FF 态（即 $\langle f \rangle_{LO} < \langle f \rangle_{FF}$）。