Yu-Xuan's Blog

前言 不得不说Mathematica中的一些颜色还是很好看的，但是当数据文件较大的时候用Mathematica绘图就会有点卡顿，不如用Python来的方便一些，这里就整理一下如何将Mathematica中的配色数据导出来，然后再加载到Python中用来绘图 首先将你喜欢的颜色数据导出来，这里可以通过改变变量dk来控制颜色间隔的大小 1234dk = 1/255;colorFunction = ColorData["LightTemperatureMap", "ColorFunction"];colorValues = Table[colorFunction[x], {x, 0, 1, dk}];Export["LightTemperatureMap.dat", colorValues, "Table"]; 将Mathematica中中导数颜色的命令封装成一个函数12345func1[colorname_] := Module[{colorFunctionlist, colorValues}, colorFunctionlist = ColorData[colorname, "ColorFunction"]; colorValues = Table[colorFunctionlist[x], {x, 0, 1, 1/255}]; Export[StringJoin[colorname, ".dat"], colorValues, "Table"];]func1["DeepSeaColors"] 执行下面的命令获取Mathematica中渐变色的名称和颜色示例12345678colornameList = Style[#, 20, Blue, FontFamily -> "Times New Roman"] & /@ ColorData["Gradients"];color = ColorData["Gradients",...

在正方晶格超导序参量自洽的文章中是利用了自洽方程得到超导序参量，并研究了其温度依赖关系。这里给出利用最小化自由能的方式来得到序参量，并给出金兹堡-朗道(Ginzburg–Landau )理论所给出的自由能随温度的演化。 公式推导起手先是一个有吸引相互作用的哈密顿量 H=\sum_{\mathbf{k},\mathbf{k}^\prime}c^\dagger_{\mathbf{k},s}h(\mathbf{k})_{ss^\prime}c_{\mathbf{k},s^\prime}-U\sum_{\mathbf{k},\mathbf{k}^\prime}c^\dagger_{\mathbf{k}\uparrow}c^\dagger_{-\mathbf{k}\downarrow}c_{-\mathbf{k}^\prime\downarrow}c_{\mathbf{k}^\prime\uparrow}平均场处理之后分解到超导通道，则可以得到BdG哈密顿量，不熟悉可以参考正常态到BdG哈密顿量的构建这篇笔记，或者参考李正中固体理论。超导序参量则需要自洽 \Delta=-U\sum_{\mathbf{k}}\langle c_{\mathbf{k}\downarrow}c_{-\mathbf{k}\uparrow}\rangle体系的自由能为 F_s=\frac{|\Delta|^2}{U}-\sum_{\mathbf{k},n}\frac{1}{2\beta}\ln(1+e^{-\beta E_n(\mathbf{k})})这里的$E_n(\mathbf{k})$就是BdG哈密顿量的本征值，BdG哈密顿量为 H_{\rm BdG}(\mathbf{k})=\left( \begin{array}{cc} h(\mathbf{k})&-i\Delta\sigma_y\\ i\Delta\sigma_y&-h^*(-\mathbf{k}) \end{array} \right)通过给定不同的$\Delta$来对角化$H_{\rm...

这里记录一下怎么在本地电脑上配对Julia的MPI库实现并行 安装Julia下载安装即可，MPI只需要在包安装环境下执行安装 123julia> import Pkgjulia> Pkg.add("MPI") 安装完成之后，在用户的主目录下(主目录直接执行cd进入即可)会存在一个隐藏的.julia文件夹，这里前面有个英文句号，进入这个文件夹显示如下 所有安装的包都会整合在packages中，进入其中就可以找到安装好的MPI 进入到MPI文件夹(中间会存在一个奇怪的文件夹，直接进入即可)的bin目录中就可以找到mpiexejl这个执行julia进行MPI并行的执行命令了，接下来就是将这个路径在.zshrc中追加到PATH里面就能够使用了 1export PATH="/Users/Yourname/.julia/packages/MPI/TKXAj/bin:$PATH" # Julia MPIEX 添加之后执行source .zshrc或者重启终端就能让命令生效了。 执行假如现在有一个使用了MPI并行的程序 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145using LinearAlgebra,DelimitedFiles,Printf,MPI,Dates#-------------------------------------------------------------------------------function ham(kx::Float64,ky::Float64) ...

整理一下在研究超导序参量的时候，理解傅里叶分析的一些笔记{:.info} 最近在计算电子配对序参量，其中要分析序参量的配对对称性，这个时候可以采用Fourier变换，分解到不同的$\sin(n\theta)$和$\cos(n\theta)$通道中，通过比较哪个通道的系数最大，就可以确定序参量的位相在动量空间中的依赖关系。不过一般在费米面上绘制出序参量差不多也就可以看出对称性了。 $d_{x^2-y^2}$配对首先是铜基超导中$d_{x^2-y^2}$电子配对，它的位相在动量空间的变换为 \Delta(\theta)=\cos(2\theta)考虑将展开 \cos(2\theta)=\sum_{\omega_n}C(\omega)e^{i\omega_n\theta}因为形式太简单了，所以可以手动进行Fourier展开 \cos(2\theta)=e^{i2\theta} + e^{-i2\theta}因此可以知道在 \omega=2,\qquad \omega=-2这两个频率处，Fourier展开系数$C(\omega)$会是最大的。 代码实现下面就通过代码来演示一下上面的分析 因为这里使用的是Mathematica的离散傅里叶变化，所以这里的$\omega_n$是会依赖于网格间距$dk$的，具体关于离散Fourier变化的算法自己不太懂，但使用这个方法的确是印证了上面的分析。 代码可以点击这里下载 参考文献 Kohn-Luttinger Mechanism of Superconductivity in Twisted Bilayer WSe$_2$: Gate-Tunable Unconventional Pairing Symmetry Quantum Geometric Unconventional Superconductivity 公众号相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。{:.info} Email yxliphy@gmail.com

整理一下将库仑势以及屏蔽库仑势通过Fourier变换到实空间时的衰减情况{:.info} 库伦势如果电子之间是直接的库伦相互作用， V(\boldsymbol{k})=\frac{1}{|\boldsymbol{k}|}该势能随着$\rvert \boldsymbol{k}\rvert $增加而减小，如下图所示 通过Fourier变换到实空间中 V(\boldsymbol{r})=\sum_{\boldsymbol{k}}V(\boldsymbol{k})e^{i(\boldsymbol{k}\cdot \boldsymbol{r})}这里取$y=0$进行$x$方向进行Fourier变换，得到实空间中库伦势能 可以看到在$x$比较大的时候，排斥相互作用还是比较强的。 屏蔽库伦势现在考虑屏蔽库伦势 V(\boldsymbol{k})=\frac{1}{\boldsymbol{k}}\tanh(\boldsymbol{k})该势能在$\boldsymbol{k}\rightarrow 0$的时候并不是发散的，而是趋近于一个常数，其分布如下图所示 与前面的库伦势相同，对$x$方向做Fourier变换，并取$y=0$，可以得到 此时可以看到，屏蔽库伦势能在实空间会很快衰减。 代码这里是用Mathematica做的快速Fourier变换，代码也贴一下 还有比较愚蠢的方式就是自己写程序进行上面的求和过程 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates#----------------------------------------------------------------------------------------------------------------------------@everywhere function Set_BZ(kn::Int64) ...

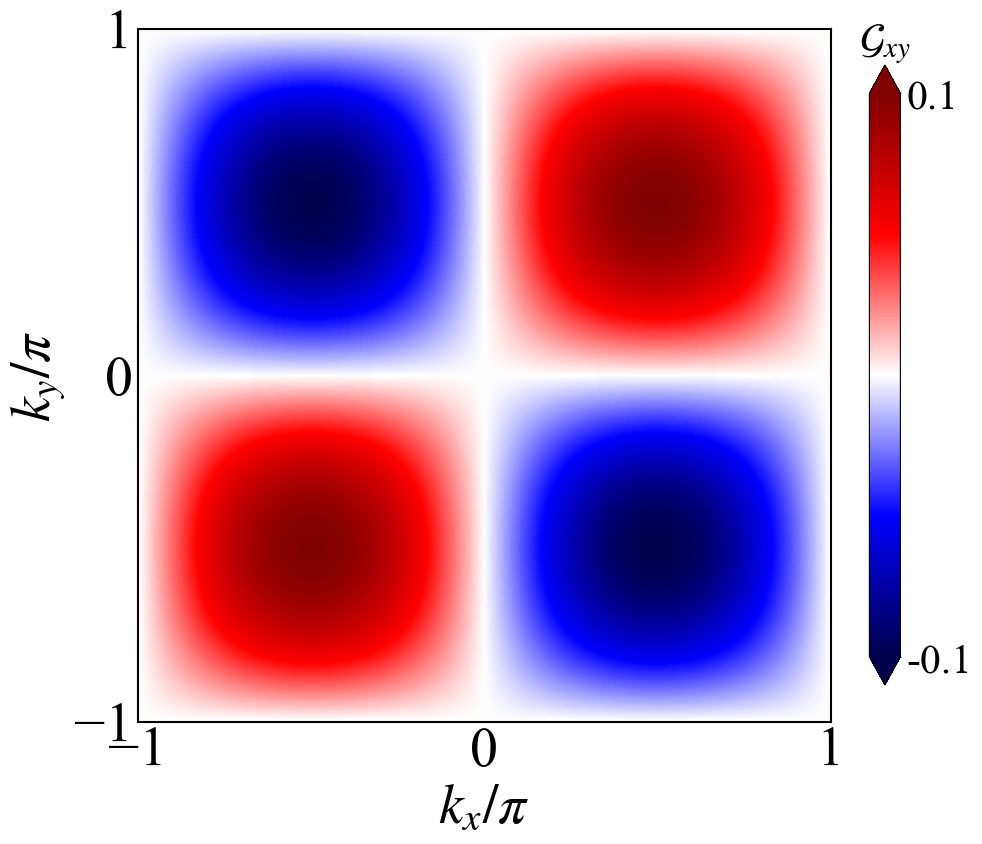
这篇博客整理了几个简单平带模型中量子度规的计算，作为学习笔记整理了一下。{:.info} 前言对于一个量子态$\lvert u(\mathbf{k}\rangle$，它的量子几何张量为 \begin{equation} \!\!\mathfrak{G}_{ab}\!=\!\langle\partial_{a}u(\mathbf{k})|\partial_{b}u(\mathbf{k})\rangle-\langle\partial_{a}u(\mathbf{k})|u(\mathbf{k})\rangle\langle u(\mathbf{k})|\partial_{b}u(\mathbf{k})\rangle. \end{equation}而量子几何张量的实部就是量子度规 \begin{equation} \mathcal{G}_{ab}(\mathbf{k})=\mathrm{Re}\left[\langle\partial_{a}u(\mathbf{k})\vert\partial_{b}u(\mathbf{k})\rangle-\langle\partial_{a}u(\mathbf{k})\vert u(\mathbf{k})\rangle\langle u(\mathbf{k})\vert\partial_{b}u(\mathbf{k})\rangle\right], \end{equation}度规可调的平带模型考虑一个拓扑平庸但是度规可调的平带模型 \begin{equation} h_s(\mathbf{k})=-t [\sin(\alpha_{\mathbf{k}})\lambda_x+ s_z \cos(\alpha_{\mathbf{k}})\lambda_y]+[-2t_2(\cos k_x+\cos k_y)-\mu]\lambda_0~, \end{equation}其中$\alpha(\mathbf{k})=\chi[\cos(k_x a)+\cos(k_y a)]$, $t_2$是最近邻跃迁大小，$\mu$是化学势，$s=\{ \uparrow,\downarrow \}$是自旋指标$s_z=\pm...