重学凝聚态拓扑(Class 7)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 Hamiltonians with para...
重学凝聚态拓扑(Class 6)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 Majorana zero modes in...
重学凝聚态拓扑(Class 5)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 From Kitaev model to a...
重学凝聚态拓扑(Class 4)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 Topological phases fro...
重学凝聚态拓扑(Class 3)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 Fermion parity switche...
重学凝聚态拓扑(Class 1)
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 能带结构在量子力学描述电子运动的时候,电子波...
$\LaTeX$中插入代码
最近在适用自己的$\LaTeX$模版整理笔记的时候,想要把自己的笔记和代码整理到一起,这样就不会时间久了笔记找得到反而代码找不到了,整理到一起就更方便了,这里就找到了一个在$\LaTeX$中插入...
分数约瑟夫森效应(Fraction Josephson Effect)
拓扑超导中存在Majorana费米子时,因为其满足非阿贝尔统计,会出现$4\pi$-Josephson效应。这里就研究Kitaev模型中的Josephson效应。 前言这里是想实现一个有Ki...
SU(2)群与SO(3)群之间的关系
在考虑空间坐标转动的时候,不可避免的遇到了欧拉转动的问题,借着这个机会整理一下SO(3)群和SU(2)之间的关系。 对于三维空间中的转动操作,可以利用欧拉转动操作来实现,这里转动按照右手系为...
Surface States of topological insulator
这里来重复Surface States of topological insulator这片文章中的一个推到,因为在学习边界态理论的过程中始终会提及到这篇文章,而且其中的内容对理解表面态还是很有...
Vortex Majorana
马上轮到大组会了,整理了一下自己关于vortex Majorana的一些基本知识和实验内容,先把PPT放在这里吧,整理过程中自己也把一些事情搞明白了,算是小有收获。 ...
稀疏矩阵少量本征值求解踩坑
最近这两天对角化矩阵本征值的时候踩了大坑,这里必须整理一下。使用的是Julia的Arpack库中,求解少量本征值的函数eigs。本来以为是自己程序写错了,认真检查了两天了,结果是这个函数自身的问...






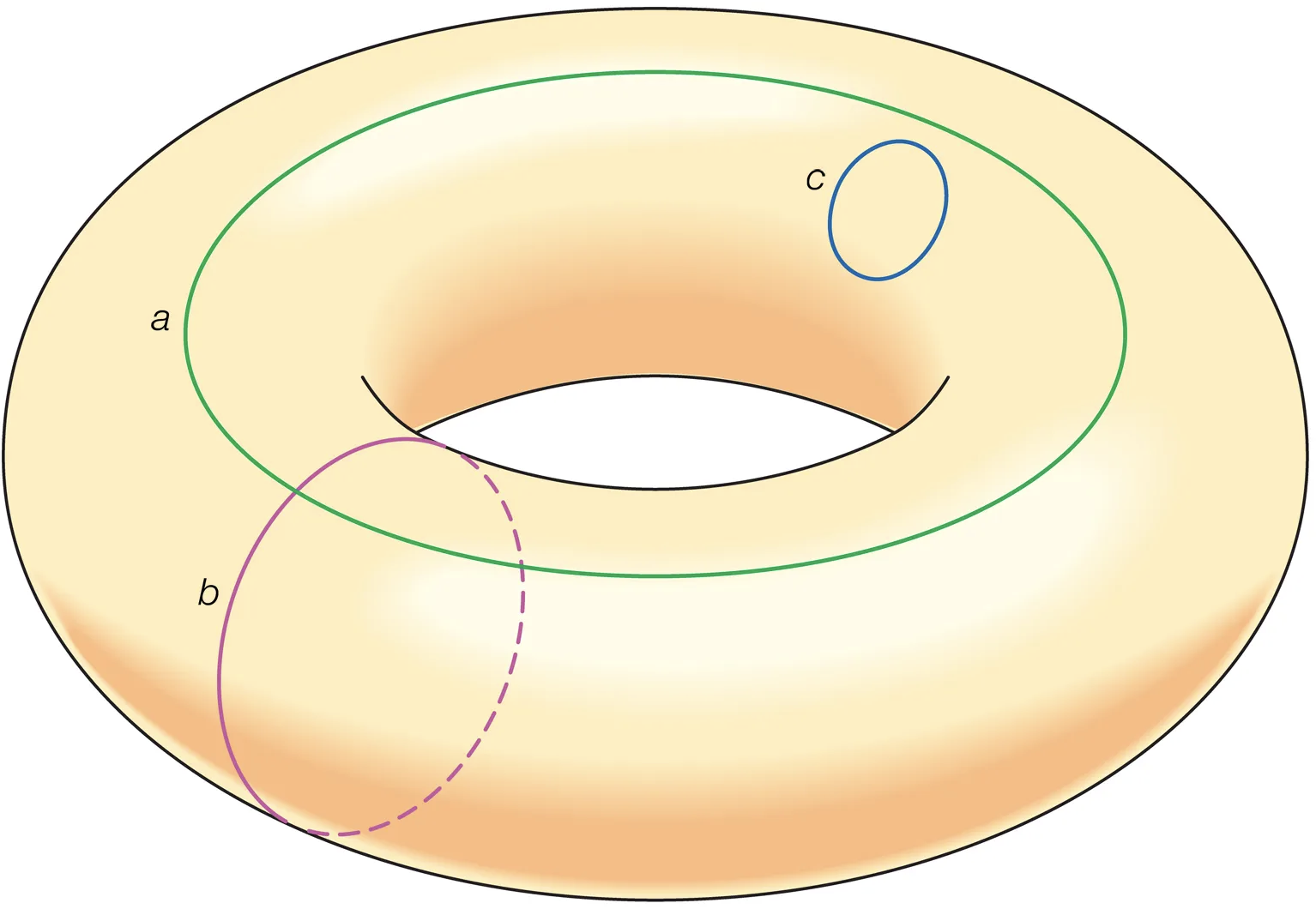
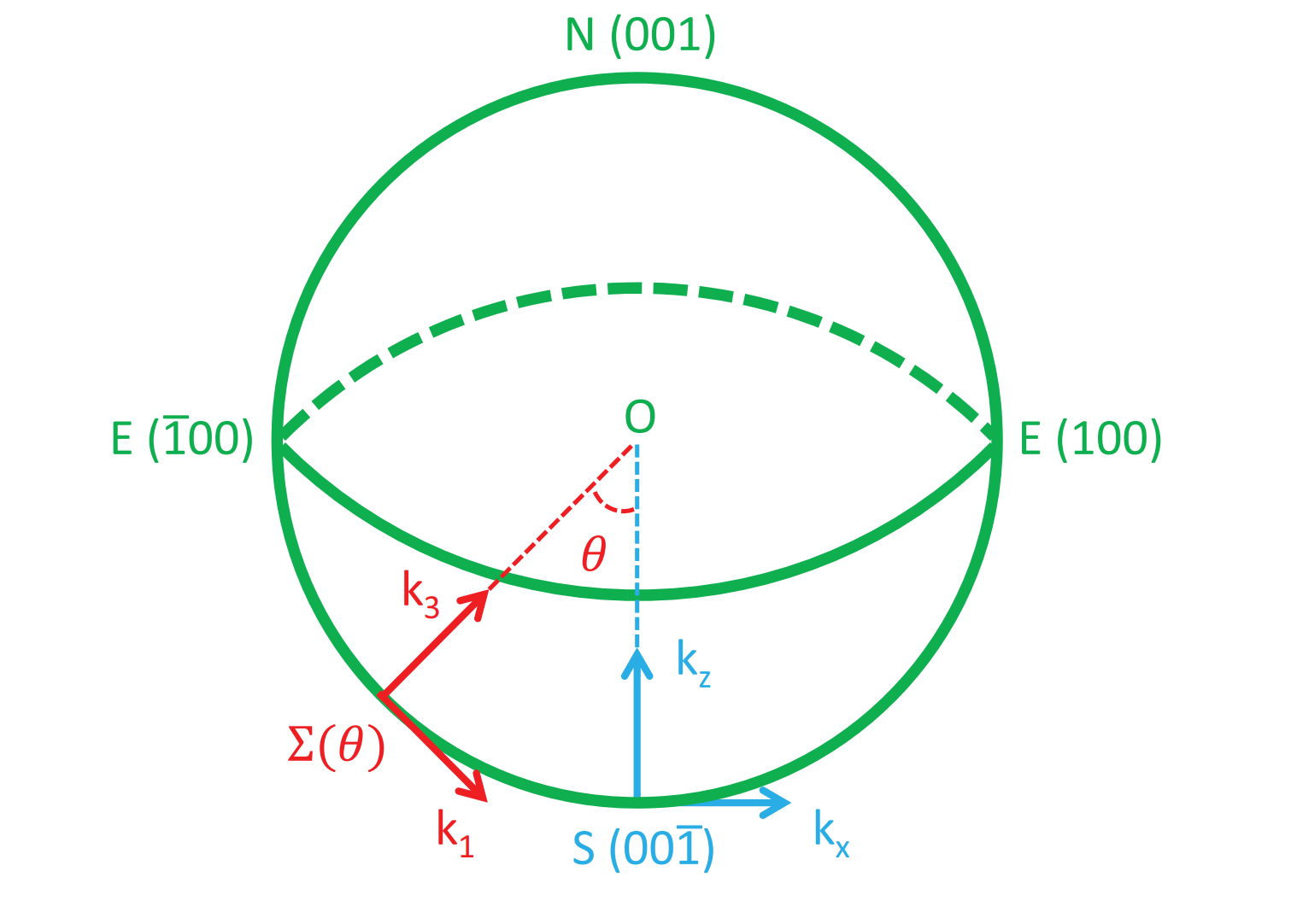


![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

