Kitaev Chain计算学习
最近重新学习关于拓扑超导的知识,先整理一下学Kitaev $p$-wave 模型的计算代码。 模型介绍Kitaev链是最简单的1D spinless $p$-wave 超导模型,和正常态的S...
APS revtex模版使用中的神神奇奇的操作
研究生期间的第一篇工作最后要使用revtex4这个模板来写,再整理内容的过程中也遇到了一些问题,比如补充材料中的公式编号修改,以及在往arxiv上传文件时候,可以把补充材料和正文放在一起,我最初...
根据哈密顿量获得其对称操作算符
通常给出的一个哈密顿量,它的对称性可能是比较高的,有时候在看文章的时候可能也并不会将哈密顿量满足的所有对称性都列举出来,但是在分析问题的时候总是会用到这些对称性,这里就整理个程序分析一下如果哈密...
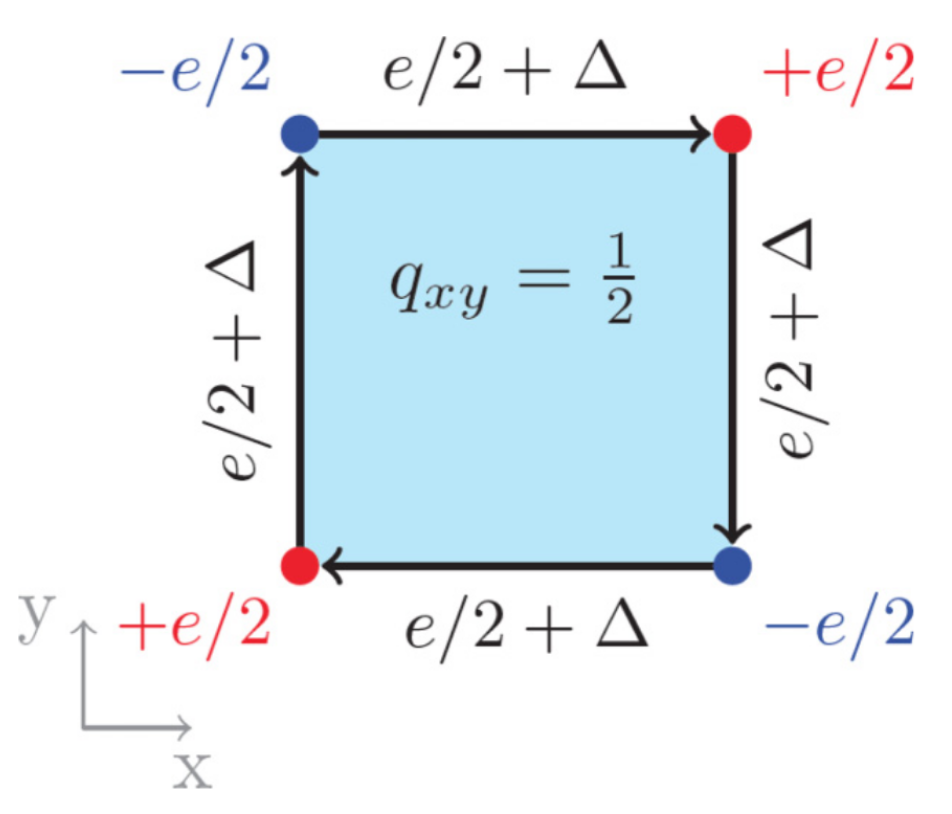
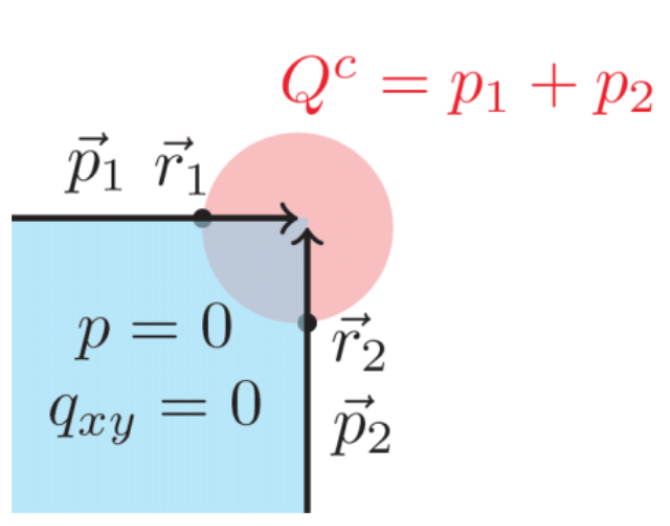
根据对称性计算体系电四极矩
这里整理一下如何通过Wannier band basis的高对称点对称性本征值来计算体系的电四极矩。想使用这个方法的主要原因是在计算Nested Wilson loop得到电四极矩的时候,如果占...
高对称路径能带图
通常为了看是否发生拓扑相变需要关注参数演化的时候能带是否发生了闭合,而且也只需要关注布里渊区高对称路径上的能带演化即可,这里就整理了自己的一个小程序,方便自己在研究问题的时候直接拿来就使用。 ...
Nested Wilson loop
继续通过Wilson loop的理解,整理出如何计算Nested Wilson loop以及其物理含义。 Nested Wilson loop在计算高阶拓扑绝缘体的时候,其边界态被打开了能隙...
边界极化
在计算发生边界拓扑相变的高阶拓扑绝缘体的时候, 有时候会遇到需要计算体系的边界极化, 其实也就是要在一个cylinder结构上计算其对应的Wilson loop, 并计算每个格点上对极化的贡献,...
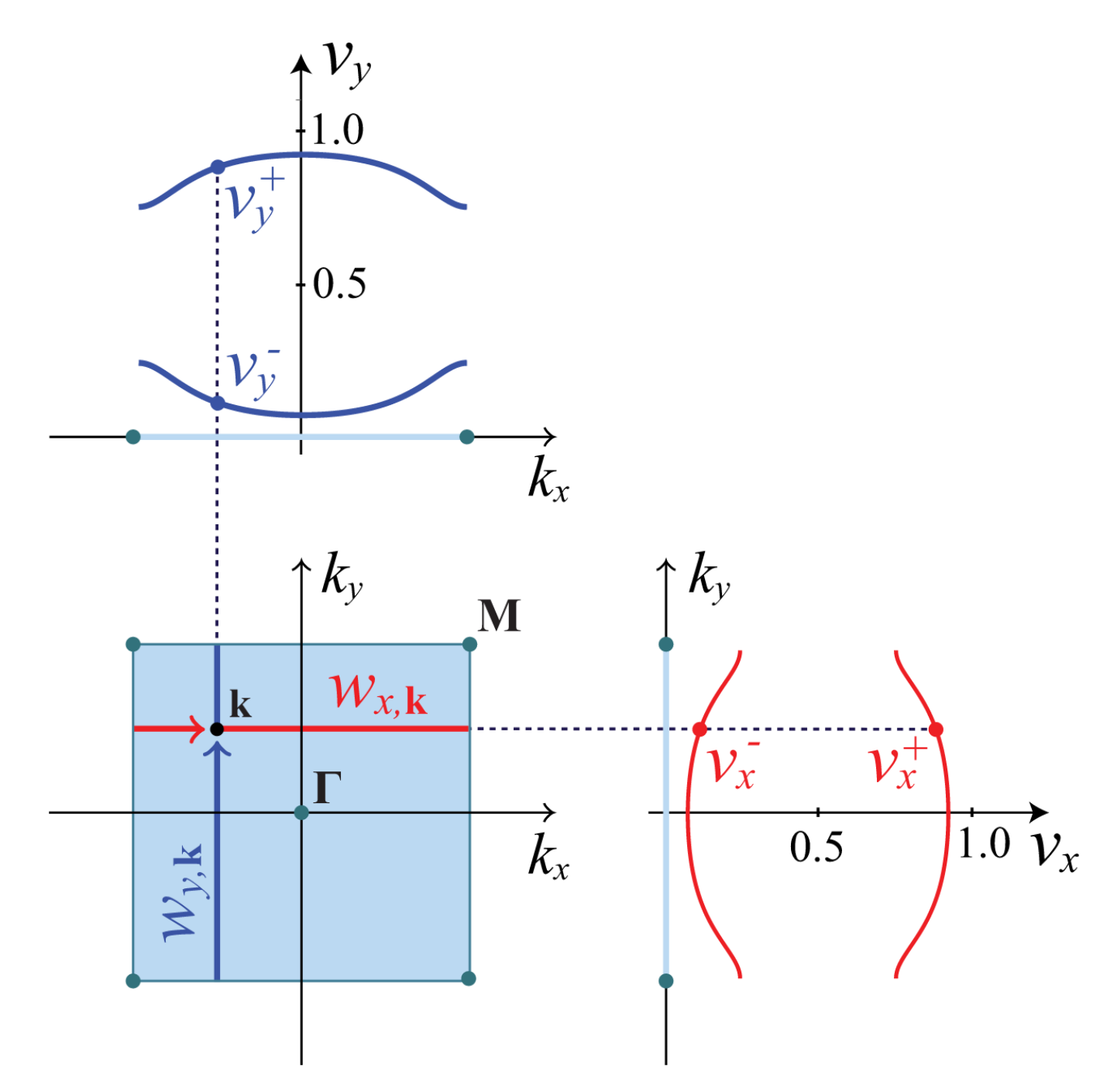
重学Wilson loop
这里整理一下自己在重新学习高阶拓扑过程中,对Wilson loop以及相关内容的一个重新理解,也为后面理解Nested Wilson loop做一个铺垫。 重学Wilson loop最近重读...
笔记模板(Latex)
在科研中我通常需要整理一些笔记,虽然也想用iPad来整理,但是排版上总是不尽人意,字写得也不好看,所以干脆就整理一个Latex模板专门整理学习笔记.这篇Blog就是将自己的这个模板分享出来,主要...
科研日志模板(Latex)
平时在阅读文献或者组会讨论的时候总会有一些需要记录的内容,这里就修改了别人的一个模板,整理了一个适合自己的记录科研log的Latex模板。 Research-Log这是用来整理平时科研过程中...
Fortran计算选择区间内本征值
在进行数值计算的时候,对于较大的矩阵,有时候并不完全需要其所有的本征值,而只需要一定范围内的本征值即可,这里就整理一下如何利用Fortran来得到选定区间内的本征值 这里其实就是使用CHEE...
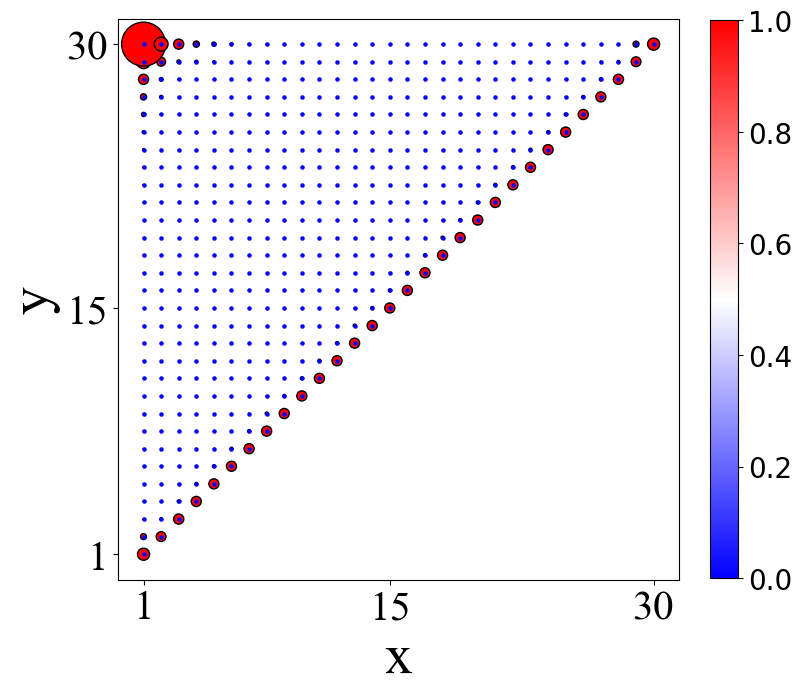
实空间上三角形状格点哈密顿量构建及求解
这里在实空间中构建一个上三角形状来计算一些系统的性质。 前言虽然自己经常研究的是正方点阵体系,但是有时候还是需要在一些特殊的形状上来计算系统的性质,这里就来构建一个上三角的格点模型来计算。 ...








![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

