BdG局域电子态密度推导
这里想通过最简单的BdG哈密顿量来推导出实空间局域电子态密度的计算公式。{:.info} Bogoliubov变换这里想通过最简单的BdG哈密顿量来推导出实空间局域电子态密度的计算公式,首先最简单的一个超导BdG哈密顿量为 \begin{equation} \mathcal{H}=-\sum_{ij\sigma}(t_{ij}c^\dagger_{i\sigma}c_{j\sigma}+\text{h.c.})+\sum_{ij}(\Delta_{ij}c^\dagger_{i\uparrow}c^\dagger_{j\downarrow}+\text{h.c.})\label{e1} \end{equation}如果将其表示为矩阵形式则有 \begin{equation} \mathcal{H}=\sum_{ij}\psi_i^\dagger H_{ij}\psi_j \end{equation}这里$\psi^\dagger_i=(c^\dagger_{i\uparrow},c^\dagger_{i\downarrow},c_{i\uparrow},c_{i\downarrow})$是Nambu表象下的基矢,为了将超导哈密顿量(\ref{e1})对角化,使用Bogoliubov变化 \begin{equation} \begin{aligned} c_{i\sigma}&=\sum_n(u_{i\sigma}^n\gamma_n-\sigma v_{i\sigma}^{n*}\gamma_n^\dagger)\\ c^\dagger_{i\sigma}&=\sum_n(u_{i\sigma}^{n*}\gamma_n^\dagger-\sigma v_{i\sigma}^{n}\gamma_n)\\ \end{aligned}\label{e3} \end{equation}这里的$\sigma=\pm...
STM到底测量的是什么
这里整理一下到底实验中的STM测量的是什么物理量。{:.info}在STM的测量中,针尖与样品之间的隧穿电流大小为 \begin{equation} I\sim\int_0^{eV_B}\rho_T(eV-E)\rho_S(\mathbf{r}_T,E)T(z,eV,E)dE \end{equation}可以看到这个电流的大小依赖于针尖的态密度$\rho_T$和样品的态密度$\rho_T$以及两者之间的转移几率$T$,而能量为$E$的电子从样品到针尖的转移几率为 \begin{equation} T(z,eV,E)=\exp(-z(\mathbf{r})\sqrt{\frac{4m}{h^2}(\Phi_T+\Phi_S+eV-2E)}) \end{equation}这里先假设针尖的态密度是个常数,可以计算$dI/dV$谱 \begin{equation} \frac{dI}{dV}|_{V_s}\sim\rho_S(eV_B)T(z,eV)+\int_0^{eV_B}\rho_S(E)\frac{\partial T(eV,E)}{\partial V}dE \end{equation}上式中的第二项是来自于高能的贡献,此时可以忽略它,从而就可以只关心样品的态密度$\rho_S$和隧穿几率$T$就可以 \begin{equation} \frac{dI}{dV}|_{V_s}\sim\rho_S(eV_B)T(z,eV) \end{equation}就是所谓的微分电导。 公众号相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。{:.info} Email yxliphy@gmail.com
Graphene 紧束缚模型推导
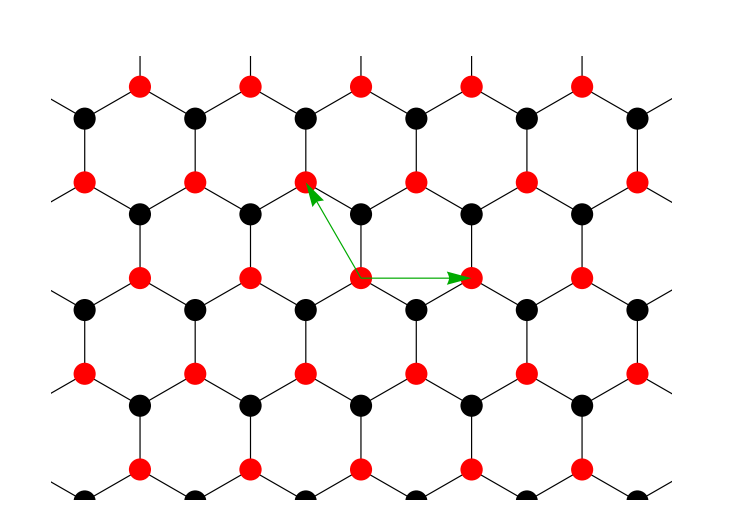
这里整理一下如何推导Graphene的紧束缚模型哈密顿量。{:.info} 晶格结构首先来分析石墨烯的晶体结构 每个原胞中包含两个不等价的C原子,晶格基矢选择为 a_1=(\frac{3}{2},\frac{\sqrt{3}}{2})a\quad a_2=(\frac{3}{2},-\frac{\sqrt{3}}{2})a这里的$a$是晶格常数,对应的到空间基矢可以计算得到 b_1=(\frac{2\pi}{3},\frac{2\sqrt{3}}{3})/a\quad b_2=(\frac{2\pi}{3},-\frac{2\sqrt{3}}{3})/a每个原子到其最近邻原子之间(不等价原子)的距离为 r_1=(\frac{1}{2},\frac{\sqrt{3}}{2})a\quad r_2=(\frac{1}{2},-\frac{\sqrt{3}}{2})a\quad r_3=(0,-1)a通过固体物理的知识,Bloch态与Wannier态之间为Fourier变换关系 \psi_{nl}(r)=\frac{1}{\sqrt{N}}\sum_le^{ik\cdot l}W_n(r,l)这里的$W_n(r,l)$就是关于$(r-l)$的Wannier函数,在这里先不考虑多条能带的情况,所以将能带指标$n$先略去,此时因为每个原胞中包含两个C原子,而且它们对应的空间位置是不等价的,可以分别给每个不等价的C原子给定一个Bloch态 \varphi_1=\frac{1}{\sqrt{N}}\sum_le^{i\mathbf{k}\cdot \mathbf{R}^A_l}\phi(\mathbf{r}-\mathbf{R}_l^A)\quad \varphi_2=\frac{1}{\sqrt{N}}\sum_le^{i\mathbf{k}\cdot...
通过python读取EIGENVAL获取wannier90构造tb模型的冻窗口和解纠缠窗口
在通过Wannier90构建tb模型的时候,总是需要比较好的确定冻窗口和解纠缠窗口,而且这两个窗口的选取会很大的影响构造的tb的好坏,这里就想通过代码,先粗略的估计一下这两个能量窗口的范围,再通过进一步的细致调节来构造处比较好的tb模型。{:.info} 获取价带和导带在构造Wannier的时候,首先需要明确的就是想要构造那一部分能带的Wannier,通常就是费米面附近的能带,这对研究很多性质都是非常重要的。首先是通过fatband分析,看看在费米面附近主要是哪些原子的那些轨道产生了贡献,以Bi为例,原胞中含有两个Bi原子,通过fatbang分析发现费米面附近主要是由$s,p_x,p_y,p_z$轨道贡献,而且体系是考虑SOC的,所有在构建Wannier的时候需要考虑的能带的数目就是 2*(1+1+1+1)*2 = 16这里的第一个2表示原胞中的两个Bi原子,四个1则是代表4条轨道,最后的2是因为考虑的SOC,所以还是需要考虑每条轨道的自旋自由度。 在确定了要构建的Wannier能带的数目之后,下面的一步就是要确定费米面的位置,这个值通过是可以在VASP计算的OUTCAR中得到的1cat OUTCAR |grep E-fermi|awk 'BEGIN {FS=" "} {print $3}' # 从OUTCAR中提取自洽计算的费米能在得到了费米能之后,就可以进一步通过EIGENVAL中的结果来确定每个k点上的能量,将所有的k点连接起来就是一条能带,可以获取每条能带的带顶和带底,通过与费米能量的比较就可以知道哪些带是占据能带(价带),哪些带是空带(导带)。123456789101112131415161718192021222324252627282930313233343536373839404142434445464748import numpy as npimport matplotlib.pyplot as pltimport osdef valread(): """通过读取EIGENVAL文件来获取每条能带的最大值和最小值""" os.chdir(os.getcwd()) #...