Yu-Xuan's Blog

这里整理一下到底实验中的STM测量的是什么物理量。 在STM的测量中，针尖与样品之间的隧穿电流大小为 \begin{equation} I\sim\int_0^{eV_B}\rho_T(e...

最近学了一下如何利用Fortran来对稀疏矩阵进行并行化计算，并且得到指定数目了一些本征态和本征值。 矩阵产生1234567891011121314151617181920212223242...

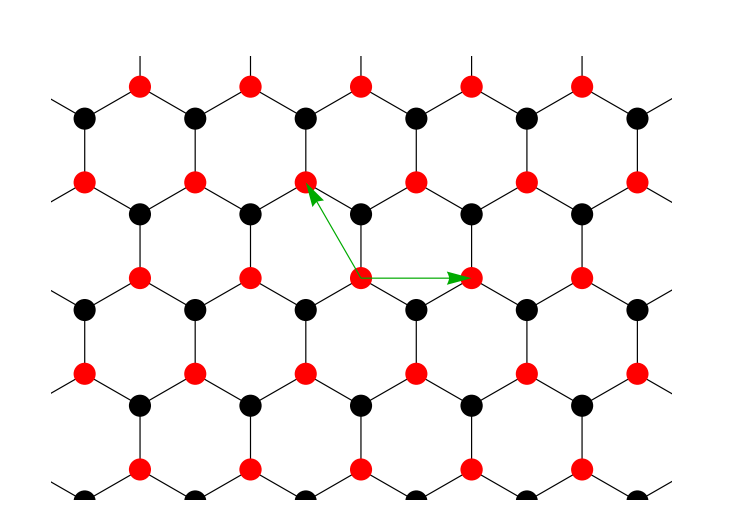
这里整理一下如何推导Graphene的紧束缚模型哈密顿量。 晶格结构首先来分析石墨烯的晶体结构 每个原胞中包含两个不等价的C原子，晶格基矢选择为 a_1=(\frac{3}{2},\fr...

这里来详细的推导一下哈密顿量在对称操作下的形式以及理解一下为什么有时候要把对称操作表示为$C_mH(k)C_m^{-1}=H(R_mk)$的形式。 哈密顿量对称变换在看文章的过程中总是不太理...

在通过Wannier90构建tb模型的时候，总是需要比较好的确定冻窗口和解纠缠窗口，而且这两个窗口的选取会很大的影响构造的tb的好坏，这里就想通过代码，先粗略的估计一下这两个能量窗口的范围，再通...

虽然之前也整理了如何计算Chern数和$Z_2$拓扑不变量,但是对于最简单的Chern Insulator却没有认真的研究过,最近在做一些和反常量子霍尔相关的一些内容,就正好把这个最简单的Che...

这篇博客主要整理一下自己在VASP使用和学习过程中遇到的错误以及如何修复这些报错. VERY BAD NEWS! internal error in subroutine IBZKPT:R...

这里整理一下通过读取紧束缚模型的hr数据，从而进一步通过之前学习到的迭代格林函数方法来计算边界态，同时也构建一个有限大小的格点来计算边界态，也算是达到对一个模型完整研究的目的。 前言之前已经...

这里整理一下自己学习使用Irvsp的过程,在捋清楚它的计算流程的同时,也希望先学会使用这个对称性分析的工具,希望之后也能做一些相关方面的工作. 对于拓扑材料的计算,在判断是否是拓扑的,通常可...

这里整理一下如何在一个方向上开边界的时候，如何求解边界态理论。 前言之前已经整理过在动量空间中求解边界态理论，这里整理一下利用另外的一种方法来求解边界态理论，主要就是将哈密顿量变换到cyli...

这里整理一下高阶拓扑的BBH模型的一些拓扑性质的计算,包括边界态,Wilson loop以及Nested Wilson loop计算. Wilson loop这个计算没有什么好说的,在其他模...

这里想整理利用VASP的POSCAR来构建一个实空间的点阵,在构建出实空间的点阵上再进行一些其他的操作. 前言在学习固体物理的过程中,其实实空间中的点阵就是利用晶格矢量来构建实空间中的周期晶...