利用Wannier90的hr数据构建动量空间能带并计算高对称点宇称
这里想整理一下如何利用已有的实空间的tight binding的数据,通过Fourier变换来得到动量空间中的模型,从而可以利用同时利用这两种不同表象下的数据进行计算研究。这里使用了BHZ模型作...
考虑次近邻之后快速迭代格林函数求解边界态
这里来整理一下在考虑了次次近邻hopping之后,如何利用迭代格林函数的方法来求解得到系统对应的边界态,这里所有的例子都是以动量空间的哈密顿量为基础,将其离散化到格点上之后进行计算的。 模型...
Helical Higne Majorana Modes in Iron-Based Superconductor
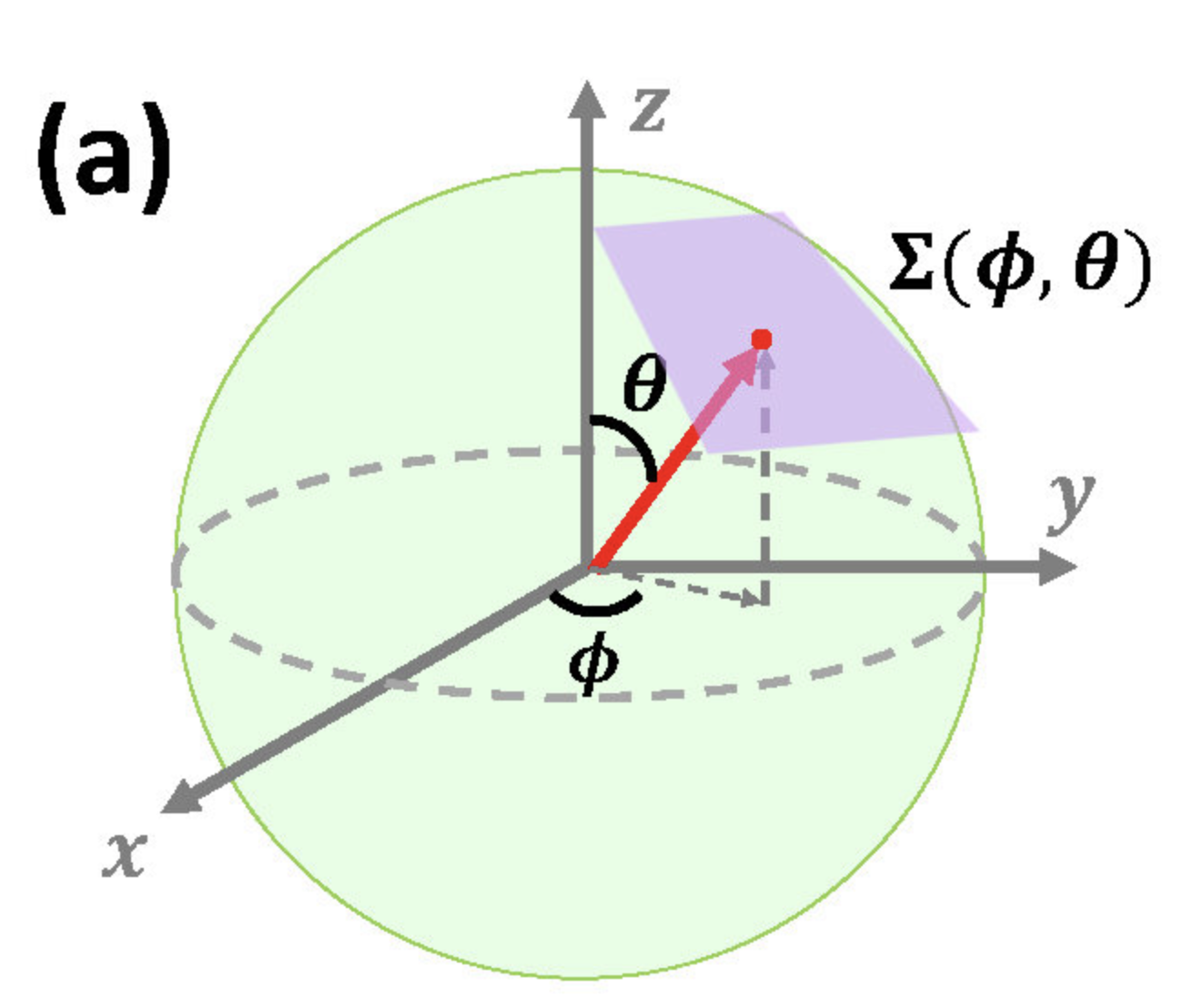
这里利用空间转动操作联系哈密顿量来推导一下如何对哈密顿量进行幺正变换从而实现对坐标系的转动,主要是Helical Higne Majorana Modes in Iron-Based Super...
利用投影子方法求解Square lattice边界态
在Square lattice上求解沿着$x$或者$y$方向求解边界态的时候,还可以使用另外一种投影子的方法,这里就介绍一下这个方法。 同样考虑BHZ模型加入Zeeman场这样的一个模型 ...
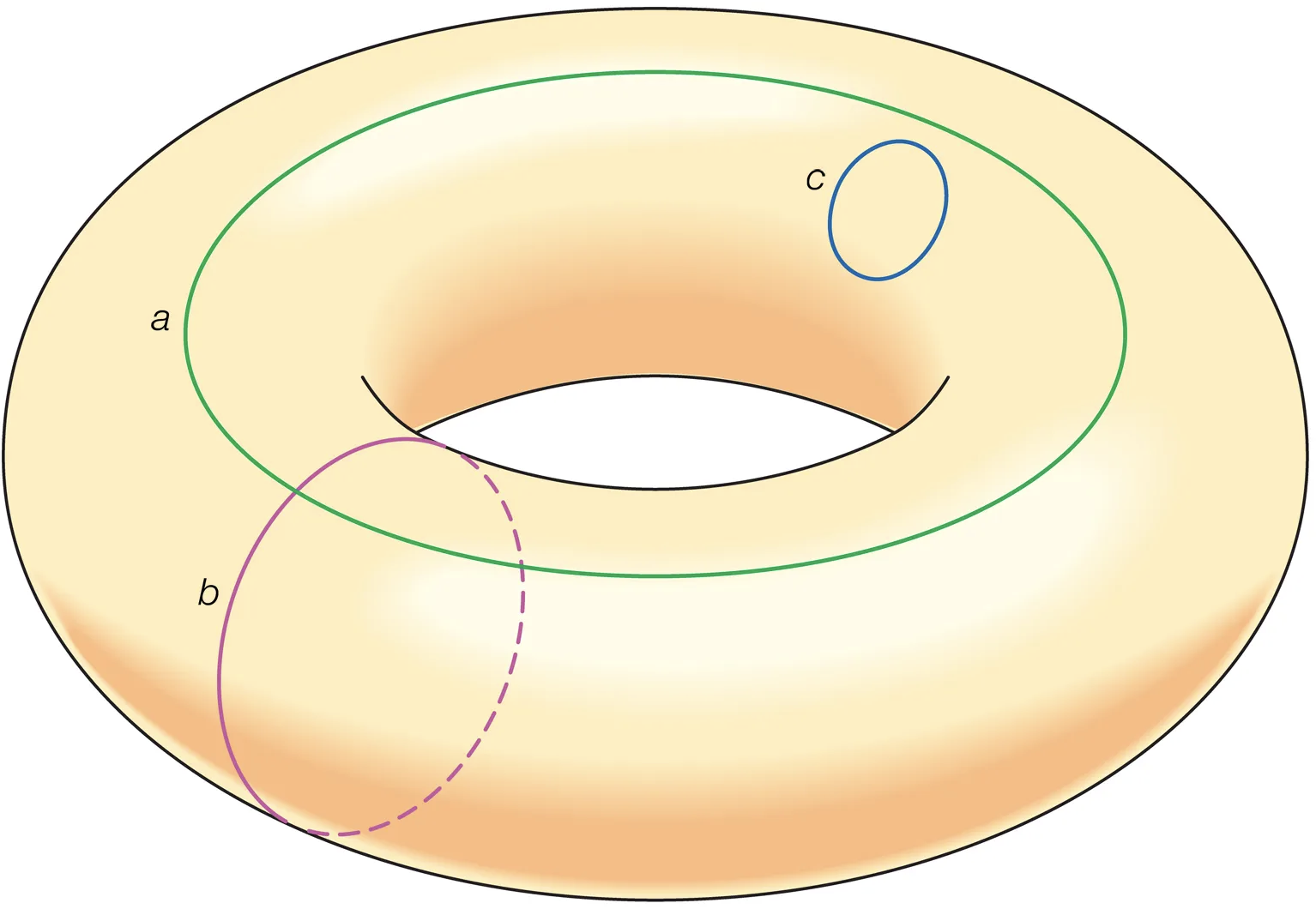
2D 环面上的边界态理论计算
最近在学习各种方式的边界态理论求解,这个博客就整理一下如何在一个2D的环面上求解边界态理论。 这里就采用最熟悉的BHZ模型,再考虑一项Zeeman场$h_0s_x$。 H(\mat...
群论学习笔记-Part6
根据不变子群的表示来得到群的表示. 诱导表示假设\mathbf{K}_1是\mathbf{G}的子群,不一定是不变子群,比如\mathbf{G}是空间群,\mathbf{K}_1是某个波矢\...
VASP输出文件内容结构解析(未完成)
这里整理一下最近学习vasp的时候,对一些输出文件中的内容进行一下整理,这样可以让自己再可视化结果的时候,明白需要从哪个文件中寻找什么结果. EIGENVAL这个文件中会输出对应$k$点的本...
Wannier90学习过程
最近在慢慢接触第一性计算的相关内容,需要补充一些工具,这里就整理记录一下我在学习Wannier90过程中遇到的疑问和自己对其中内容的一些理解. 我在这里完全就先是重复Wannier90给出的...
群论学习笔记-Part5
空间群操作对Bloch函数的影响以及空间群的表示 空间群操作对Bloch函数的作用对一个空间群操作 \{S\rvert\mathbf{w}\}\psi(\mathbf{r}=\psi(S^{...
群论学习笔记-Part4
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解. 平移群不可约表示每个空间群都有一个不变子群$\math...
群论学习笔记-Part3
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解. 空间群空间群$\mathbf{G}$包含了纯平移操作$...
Latex中特殊符号收集
这里收集了一些在平时写Latex的时候可能用到的一些符号。 鉴于该网站分享的大都是学习笔记,作者水平有限,若发现有问题可以发邮件给我 yxliphy@g...






![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

