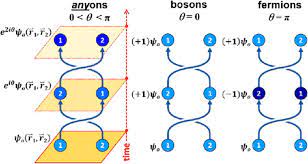
Majorana费米子
这里整理一下如何从Dirac方程出发,来衍生出Majorana费米子. Dirac方程对于一个自旋半整数的费米子,其满足Dirac方程 (i\gamma^\mu\partial_\mu-m)...
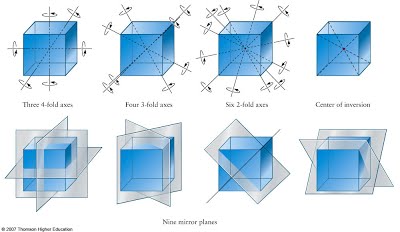
群论学习笔记-Part2
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解. 点群操作基函数球谐函数对于点群操作,可以找到对应的一些...
群论学习笔记-Part1
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解. 基本概念共轭一个元素$a,b,c$是群$\mathca...
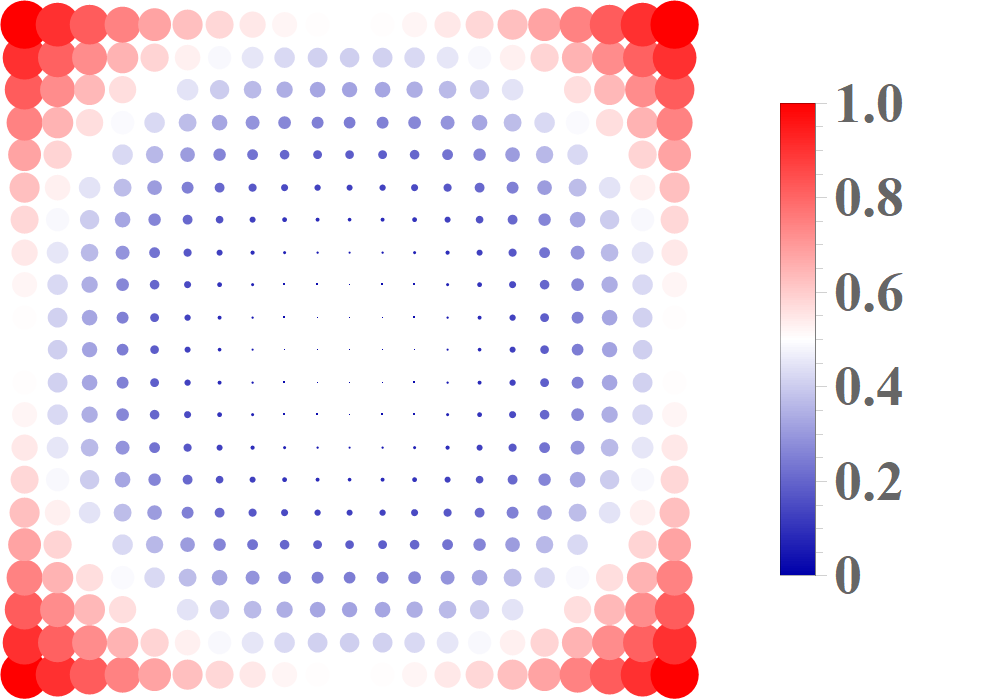
Mathematica绘制漂亮的散点密度图
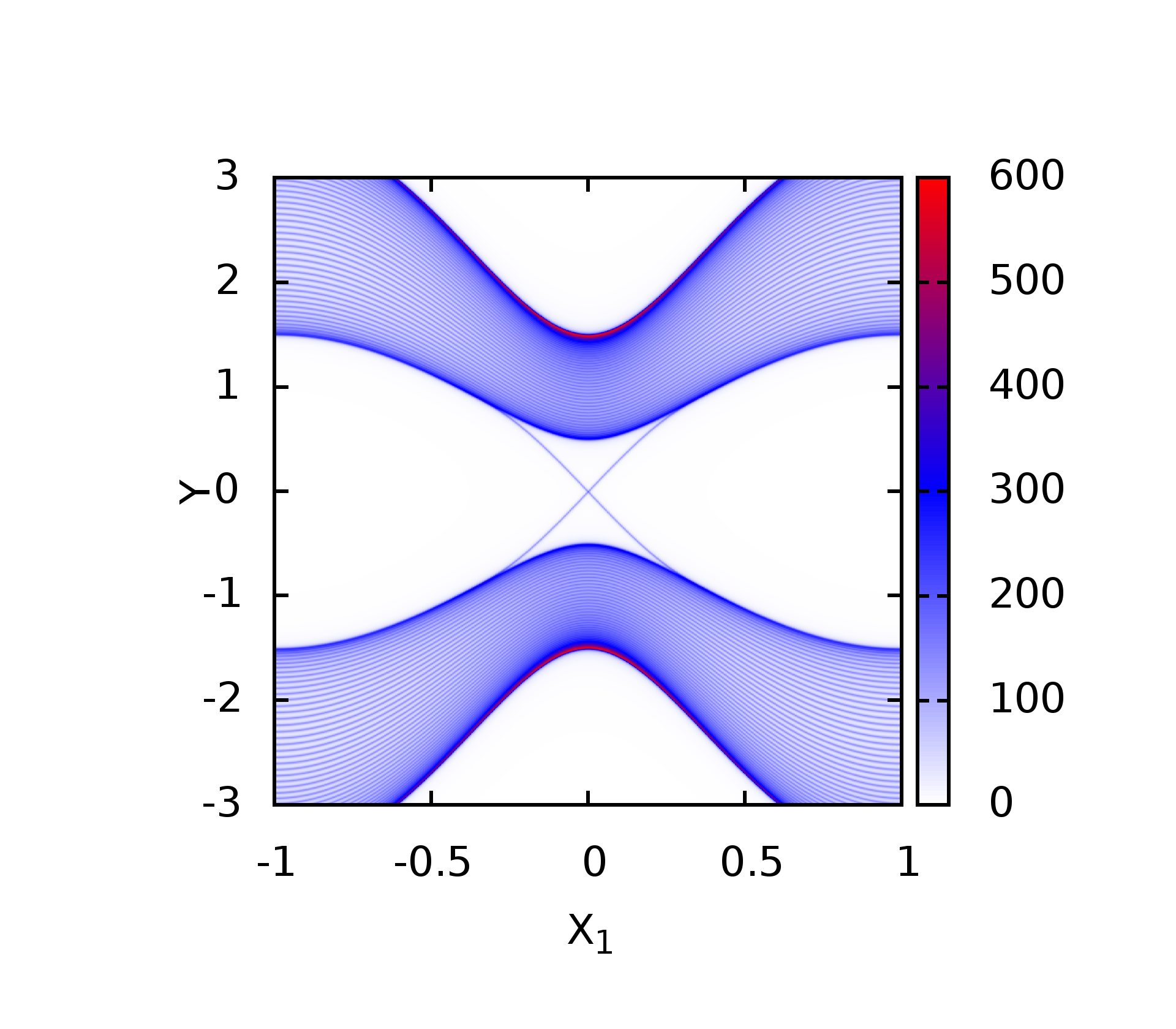
在通过计算得到二维密度图之后,如何绘制一幅漂亮的密度图,可以美观的展示自己的结果,这里就来整理一下如何利用Mathematica来绘制这样的密度图. 首先把代码贴出来 首先根据颜色进...
借助Fortran格式化Julia输出的数据
这里整理一下利用Fortran将数值计算过程中由Julia计算出的数据进行格式化输出. 在利用Julia做计算的时候,始终不能将数据整理成格式化的形式,这里就只好借助于Fortran来将其输...
利用格林函数求解边界态-V2
这篇博客中利用另外一种格林函数的方法来计算拓扑绝缘体的边界态. 在前面利用格林函数求解边界态这篇博客中利用迭代格林函数的方法计算了拓扑绝缘体的边界态,但是结果中边界态的确很明显,但是体态的性...
访问github.io网站的方法
很长一段时间,自己需要FQ才能看自己的博客,这里提供一个修改DNS服务器的方式来让自己的电脑可以访问github.io这样的网站. 自己居然不能访问自己的github.io网站,很是离谱,这...
两维非厄米体系中的Fermion Doubling Theorems
这篇博客想通过精读一片研究两维非厄米体系中的Fermion Doubling Theorems的PRL文章,同时了解厄米与非厄米体系中的Fermion Doubling Theorems到底是什...
拓扑绝缘体哈密顿量推导
这篇博客整理一下在拓扑材料Bi$_2$Se$_3$计算中,通过能带成分和对称性分析,再结合微扰论来推导低能有效模型,主要是对文章进行翻译,过程中会加一点自己的笔记. 虽然对拓扑绝缘体的材料和...
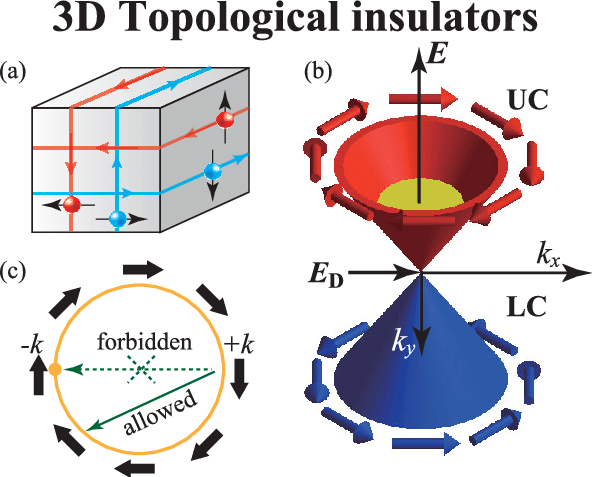
3D 拓扑绝缘体模型对称性分析及推导
虽然一直在利用2D和3D拓扑绝缘体的模型来进行一些研究,但是对这个模型的来源和对称性却并不明白是为什么,这里就来完整的整理一下到底这个模型是如何得到的,以及对应的对称性又是如何表示的。 对称...
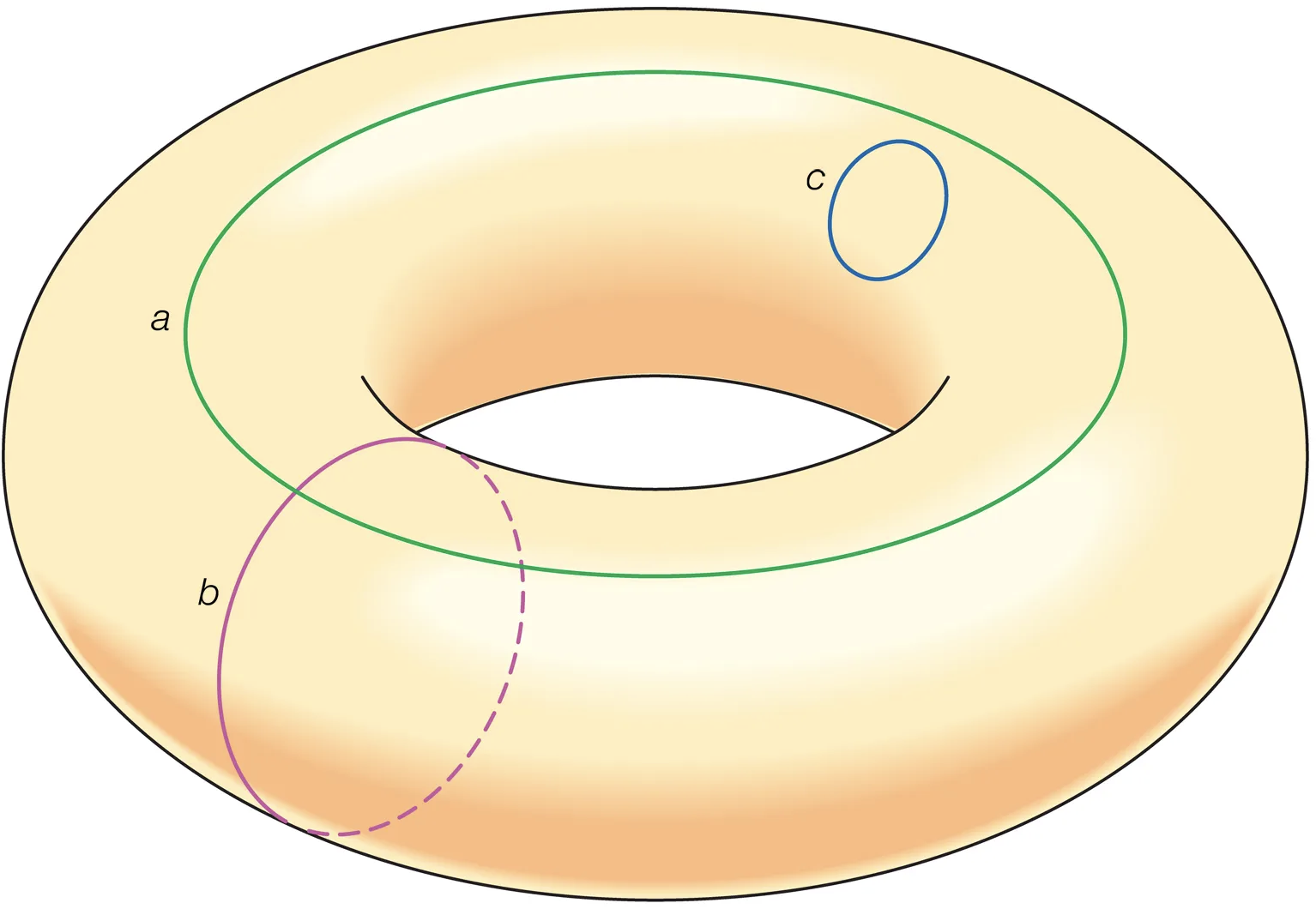
同伦概念学习(Homotopy)
同伦是在学习凝聚态拓扑的时候会遇到的一个概念,尤其是在学习拓扑分类的时候.这里就整理一下同伦这个概念,自己在学习时候的笔记. 基本概念定义一个映射 \phi:M\rightarrow T,\...
时间反演不变绝缘体的拓扑场论
这篇博客中,整理自己在学习拓扑绝缘体相关的拓扑场论过程中的一些概念整理和自己的笔记,主要是对文章进行翻译,过程中会加一点自己的笔记。 第一Chern数:对Berry 位相规范场的曲率在整个B...







![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

