群论学习笔记-Part5
空间群操作对Bloch函数的影响以及空间群的表示{:.info} 空间群操作对Bloch函数的作用对一个空间群操作 \{S\rvert\mathbf{w}\}\psi(\mathbf{r}=\psi(S^{-1}(\mathbf{r-w}))首先可以证明 \exp(i\mathbf{k}\cdot S\mathbf{r})=\exp(iS^{-1}\mathbf{k}\cdot\mathbf{r})这是因为 \mathbf{k}\cdot S\mathbf{r}=\sum_{ij}k_iS_{ij}r_j=\sum_{ij}S^T_{ji}k_ir_j=\sum_{ij}S^{-1}_{ji}k_ir_j因为$S$是点群操作,其表示是个正交矩阵满足$S^T=S^{-1}$,即可以得到 \{S\rvert\mathbf{w}\}\exp(i\mathbf{k}\cdot\mathbf{r})=\exp(i\mathbf{k}\cdot...
群论学习笔记-Part3
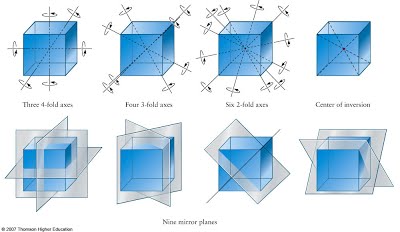
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.{:.info} 空间群空间群$\mathbf{G}$包含了纯平移操作$\{E\rvert\mathbf{t}\}$,这些平移操作构成了空间群$\mathbf{G}$的一个不变子群$\mathbf{T}$. \mathbf{t}=n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3对于实际的晶体,通常考虑周期性边界条件 \{E\rvert l_1N_1\mathbf{t}_1+l_2N_2\mathbf{t}_2+l_3N_3\mathbf{t}_3\}=\{E\rvert\mathbf{O}\}对于一个晶体,如果存在两个布拉菲点阵,那么它们之间一定是等价的,通过连续形变,一定可以将两者进行相互变换,而且在变换过程中要始终保证点阵的对称性是相同的,不能改变其对称性.下面给出14中布拉菲点阵的基矢及相关信息 每个晶系满足的对称操作如下 下面给出每个对称操作对布拉菲点阵基矢的变换关系 同样可以利用SpaceGroupIrep这个工具来得到具体的表 通过实空间的布拉菲点阵,同样可以定义出倒空间中的点阵 \mathbf{g}_i\cdot\mathbf{t}_j=2\pi\delta_{ij},\quad...
群论学习笔记-Part4
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.{:.info} 平移群不可约表示每个空间群都有一个不变子群$\mathbf{T}$,它包含了基于这个空间群的布拉菲点阵上的所有平移操作${E\rvert n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3}$,在采用周期性边界条件之后$0\le n_i<N_i,i=1,2,3$.平移操作满足${E\rvert\mathbf{t}}{E\rvert\mathbf{s}}={E\rvert\mathbf{t+s}}$,因为采用了周期性边界条件,空间群对应的平移操作可以表示为三个阶数为$N_i$的循环群的外直积$\mathbf{T}=\mathbf{T}_1\otimes\mathbf{T}_2\otimes\mathbf{T}_3$,而对于一个循环群而言,它的表示是比较容易求解得到的. 这里平移群表示为三个方向上的平移群的外直积,可以理解为这三个方向上的平移是互不影响的,也就是说无论平移的顺序如何,单独方向上的平移操作总是不会受到其他两个方向上操作的影响. 对于平移群$\mathbf{T}_1$的不可约表示$\Delta$是$N_1$个数,可以通过$p_1(0\leq p_1\leq N_1)$来标记 \Delta^{p_1}(\{E\rvert n_1\mathbf{t}_1\})=\exp(-2\pi in_1p_1/N_1)通过直积表示,就可以轻易的得到平移群$\mathbf{T}$的不可约表示,它们都是1维的,而且是$N_1N_2N_3$个数,标记$k_i=p_i/N_i$并选择$\mathbf{k}=(k_1,k_2,k_3)$作为倒空间中的矢量 \mathbf{k}=k_1\mathbf{g}_1+k_2\mathbf{g}_2+k_3\mathbf{g}_3\label{eq1}则对应的$\mathbf{T}$的不可约表示为 \Delta^\mathbf{k}[\{E\rvert...
Latex中特殊符号收集
这里收集了一些在平时写Latex的时候可能用到的一些符号。{:.info} 公众号相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。{:.info} Email yxliphy@gmail.com
Majorana费米子
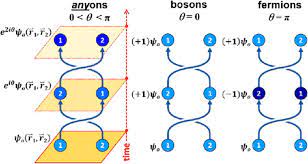
这里整理一下如何从Dirac方程出发,来衍生出Majorana费米子.{:.info} Dirac方程对于一个自旋半整数的费米子,其满足Dirac方程 (i\gamma^\mu\partial_\mu-m)\psi=0这里的$\gamma$是$4\times 4$的Dirac矩阵,满足Clifford代数关系$\{\gamma^\mu,\gamma^\nu\}=2g^{\mu\nu}$,而$g^{\mu\nu}$则是Minkowski空间中的量满足$\{-1,+1,+1,+1\},m$是真空中电子的质量,光速$c=1$选择为自然单位.这里Dirac矩阵为 \gamma^0=\sigma\otimes\tau^3,\qquad\gamma^{\mu=1,2,3}=i\sigma^\mu\otimes\tau^2这里Pauli矩阵$\sigma,\tau$分别表示自旋和电荷自由度.在量子场论的语言中,如果一个场产生了一个粒子并且消灭了它的反粒子,那么这个场的复数共轭就对应着产生一个反粒子并且消灭一个粒子.也就说$\psi\neq\psi^*$,粒子和反粒子是不相同的对应. 即从Dirac方程出发,对于任意满足Dirac方程的粒子,那么一定存在一个与之相关联的反粒子具有相同的质量和相反的电荷,这也就是提出了反粒子的概念.相对论费米子粒子都是由Dirac方程来描述的,并称为Dirac费米子. Majorana费米子Ettore...
群论学习笔记-Part2
学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.{:.info} 点群操作基函数球谐函数对于点群操作,可以找到对应的一些基函数来满足变换性质,从而在基函数的基础上可以得到操作的矩阵表示,这里就以球谐函数为出发点,来寻找点群操作的基函数.首先球谐函数的定义为 Y_l^m(\theta,\phi)=\sqrt{\frac{(2l+1)(l-\rvert m\rvert)!}{4\pi(l+\rvert m\rvert)!}}P_l^m(\cos\theta)\exp(im\phi)这里$P_l^m(\cos\theta)$是勒让德函数 P_l^m(\cos\theta)=\frac{1}{2^ll!}\sin^{\rvert m\rvert}\theta\frac{d^{l+\rvert m\rvert}}{(d\cos\theta)^{l+\rvert m\rvert}}\{(\cos^2\theta-1)^l\}一个转动操作$R$可以通过欧拉角($\alpha,\beta,\gamma$)来表示:首先进行绕z轴的主动转动角为$\alpha,(0\le\alpha\le2\pi)$,接下来绕着y轴进行主动转动$\beta,(0\le\beta\le\pi)$,最后绕着z轴主动转动$\gamma,(0\le\gamma\le 2\pi)$.在三维的求坐标系中,第一次转动$\alpha$对应着$(r,\theta,\phi)\rightarrow(r,\theta,\phi+\alpha)$,第二次转动$\beta$对应$(r,\theta,0)\rightarrow (r,\theta+\beta,0)$,第三次转动$\gamma$对应着$(r,\theta,\phi)\rightarrow...