VASP+Wannier90编译计算紧束缚能带
最近在学习利用Wannier90结合VASP来做计算,这里先整理一下如何把VASP与Wannier90进行接口,在利用Vaspwiki上的一个例子来测试一下编译好的VASP如何得到紧束缚模型的一...
Python绘图模板整理
日常科研绘图python绘图模板收集 棒棒糖图123456789101112131415161718192021222324252627282930313233343536373839404...
Fortran 常用函数及操作
因为自己在学习中最常使用的是Fortran,有时候要用到mkl库中的一些函数,但是这些函数的调用参数有很多,所以将自己常用的一些记录下来,以后忘了可以快速的查阅。 1. cheevd复厄密矩阵对...
Material Studio寻找元胞布里渊区(BZ)高对称点
最近在学习计算一些材料的能带,其中最主要的是要找到需要计算的k空间点,这里就想记录一下如何利用Material studio来通过晶体结构文件来找到BZ中的高对称点. 晶体结构文件下载我通常是从...
wannier90_hr数据的可视化分析
通常会遇到WannierTools计算紧束缚模型的问题,有时候也会遇到只有wannier90_hr.dat这个数据,那么怎么样可以通过这个数据来分析出对应的紧束缚模型到底是什么样的,这里就利用M...
从紧束缚模型出发构建WannierTools需要的数据
之前学习用WannierTools来计算一些拓扑性质,其中也涉及到了利用它来研究一个紧束缚模型的问题,这里主要是详细分析一下我们如何从紧束缚模型出发来造出WannierTools所需要的数据结构...
Willson Loop学习笔记
这篇文章主要记录一下自己学习Willson loop时候的笔记,因为他实空间中的一些物理图像非常好用,而且也和拓扑不变量是有非常深刻的联系.虽然在前面我在计算拓扑不变量的时候,也使用过Wills...
转角石墨烯摩尔纹
从转角石墨烯发现超导以来,转角已经成为了一个非常火热的研究方向,这里就简单的利用Mathematica实现转角石墨烯中的摩尔纹. 作为凝聚态物理的研究生,转角石墨烯的火热让人感受颇深,这里我...
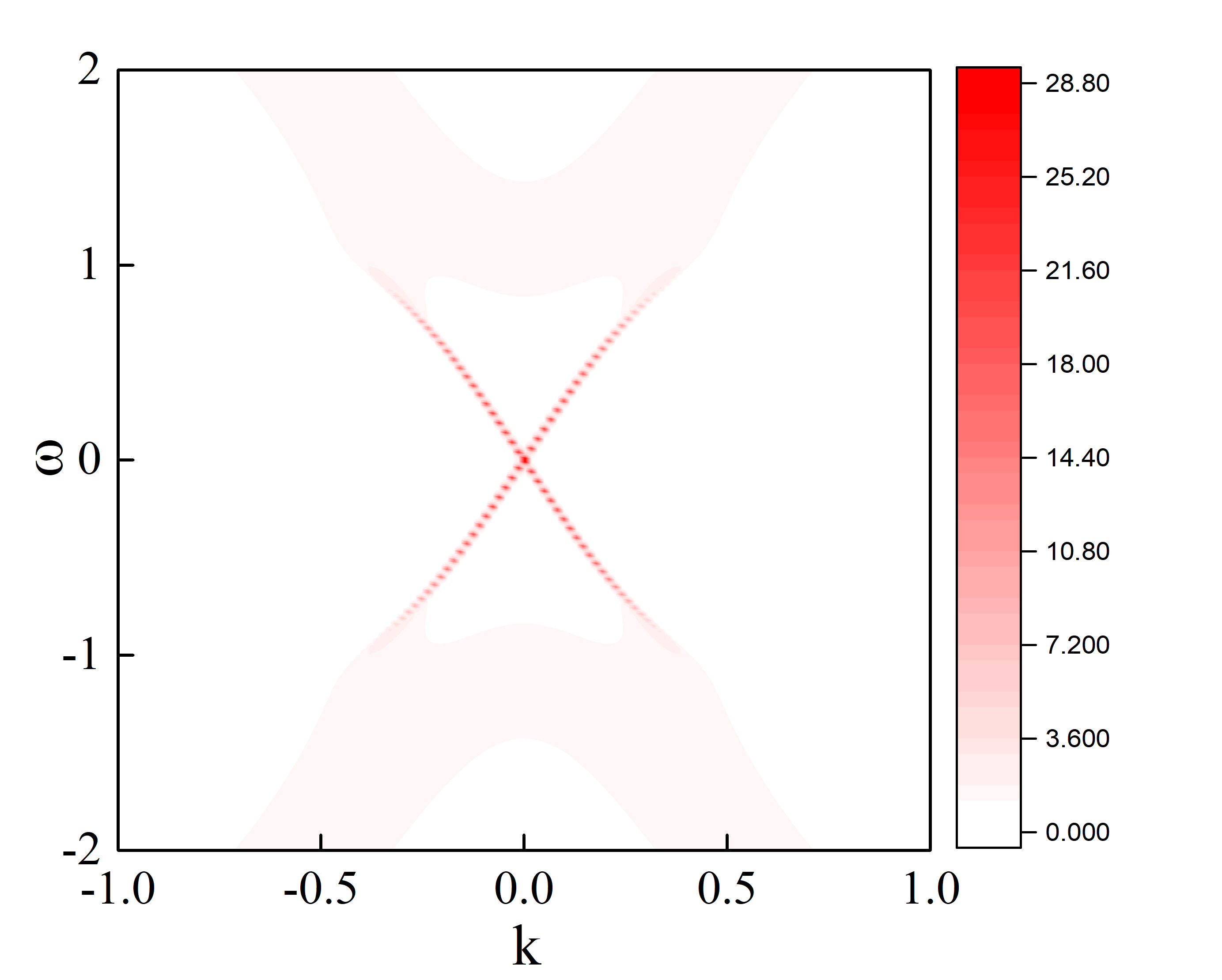
利用格林函数求解边界态-快速算法
前面的一篇博客利用表面格林函数计算了边界态,虽然相比于通常对角化哈密顿量矩阵的方法要节省之间,但是迭代的收敛速度会比较慢,这里就提供一种收敛速度更快的方法来计算边界态. 在之前的利用格林函数...
利用格林函数求解边界态
这里是利用边界格林函数方法来计算边界态,相比于通常取cylinder的方法,计算速度上是要快一些,做出来的图可以更加清晰的反映边界态的特征. 在之前的Hamiltonian构建时的基矢选择这...
从Pauli矩阵出发构造哈密顿量
学过高量及量子场论之后,总是习惯将哈密顿量写成二次量子化的形式,但是在凝聚态的能带问题中,通常看到的只是动量$k$的一个写成Pauli矩阵的表达式,这里项把这两者之间的联系建立一下,顺便对自己也...
拓扑绝缘体中任意方向表面态求解
最近在学习整理边界态理论的内容,虽然对于一般$x,y$方向开边界计算边界态在前面的博客中已经整理学习过,但是如何对任意方向开边界,并利用解析的方式来计算边界态还不是很明白,这里就整理一下自己学习...









![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

