Yu-Xuan's Blog

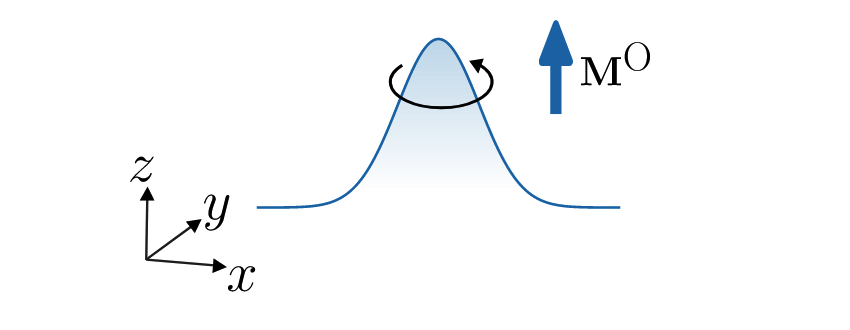
轨道磁矩推导笔记 轨道磁矩推导在量子力学中，轨道角动量的定义是 $\mathbf{L} = \mathbf{r} \times \mathbf{p}$。但在无限大的周期性晶体中，电子是弥散在整...

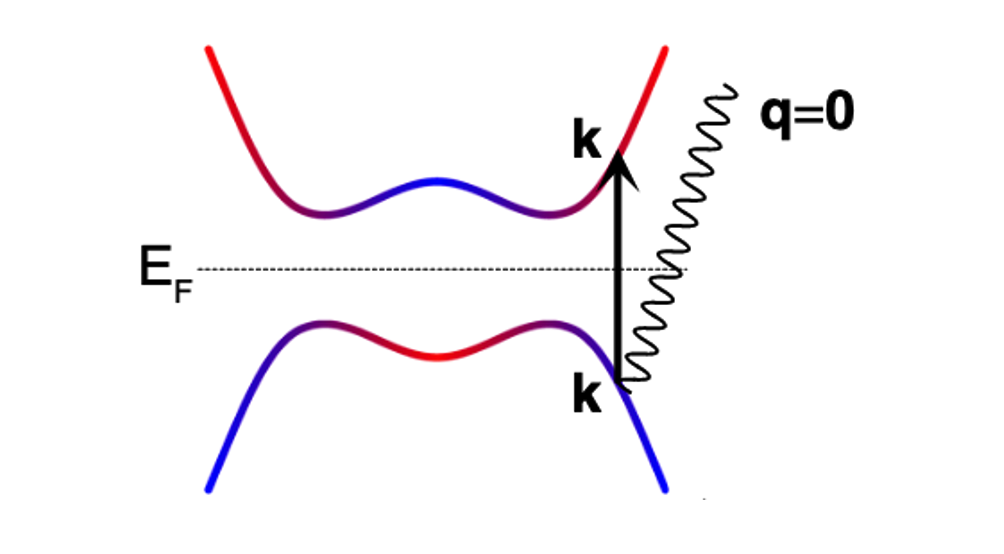
BdG 哈密顿量下的电磁响应（光电导）推导在 Nambu 空间下定义 \Psi_{\mathbf{k}} = \begin{pmatrix} c_{\mathbf{k}} \\ c_{-\ma...

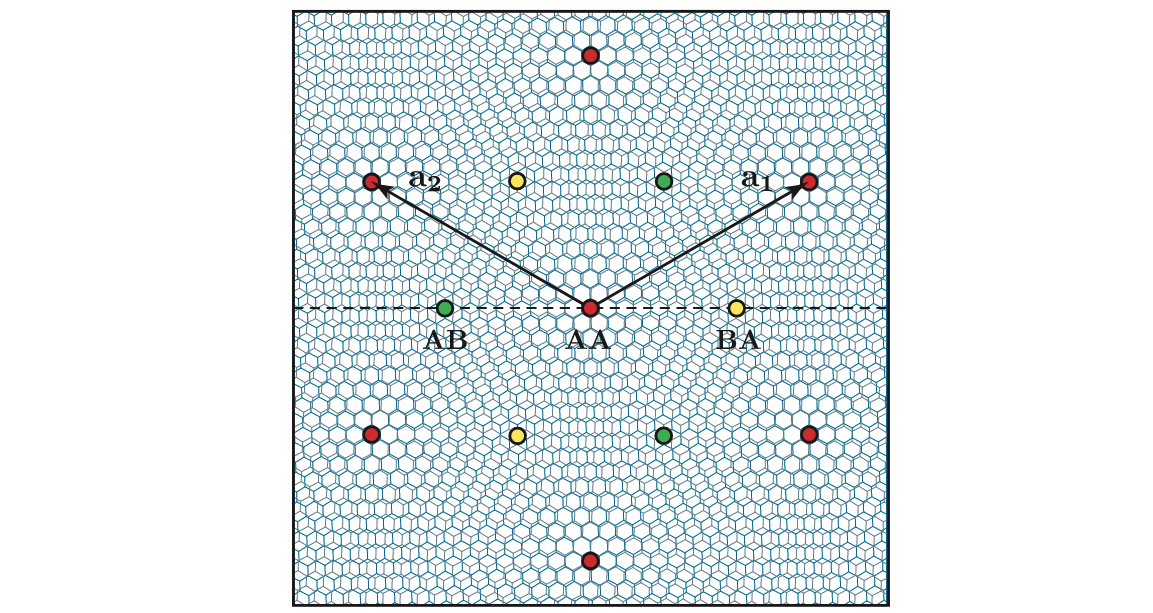
转角石墨烯学习笔记 TBG的手征极限Bistritzer–MacDonald（BM）模型为 H = \begin{pmatrix} -iv_0\, \boldsymbol{\sigma}_...

BdG 哈密顿量在不同基矢下面的形式会略有不同，但二者计算的结果都是等价的，因为二者的基矢之间也只是幺正变换联系的，这里就展示一下具体的实例。 基矢选择一选择 Nambu 基矢 \Psi^\...