Julia,Python,Fortran,Mathematica循环计算速度比较
在平时进行数值计算时,我经常会遇到的两种比较消耗时间计算,其一是对大型矩阵的对角化问题,这是在对哈密顿量厄密矩阵求解本征问题时经常遇到的;另外一个就是循环计算了,这个结构在动量空间计算体系格林函数等其它量时,也会经常遇到。在这里首先对比一下各编程语言对循环的计算速度,然后根据我的经验提供一些加速的方法。{:.info} 速度对比在这里只是简单的展示一下计算速度,所以我只是采用了三层循环嵌套,每层的循环数为1000 python1234567891011121314import timedef f1(): c = 0 cont = 1000 #控制循环的次数 for i in range(cont): for j in range(cont): for k in range(cont): c = c + i + j + k return ct1 = time.time()print(f1()) # 计算循环求和t2 = time.time()print('Timing cost is(s): ',t2 - t1) Result is: 1498500000000Timing cost is(s): 85.73423385620117 julia123456789101112function sum1(num::Int128) c::Int64 = 0 for i in 0:num-1 for j in 0:num-1 for k in 0:num-1 c = c + i + j + k end end end return cend@time sum1(999) Result is: 1498500000000 Timing cost is(s): 0.000084 seconds Fortran123456789101112131415161718192021program mainimplicit noneinteger i,j,k,continteger(kind = 8) creal...
RPA(Random Phase Approximiation)推导
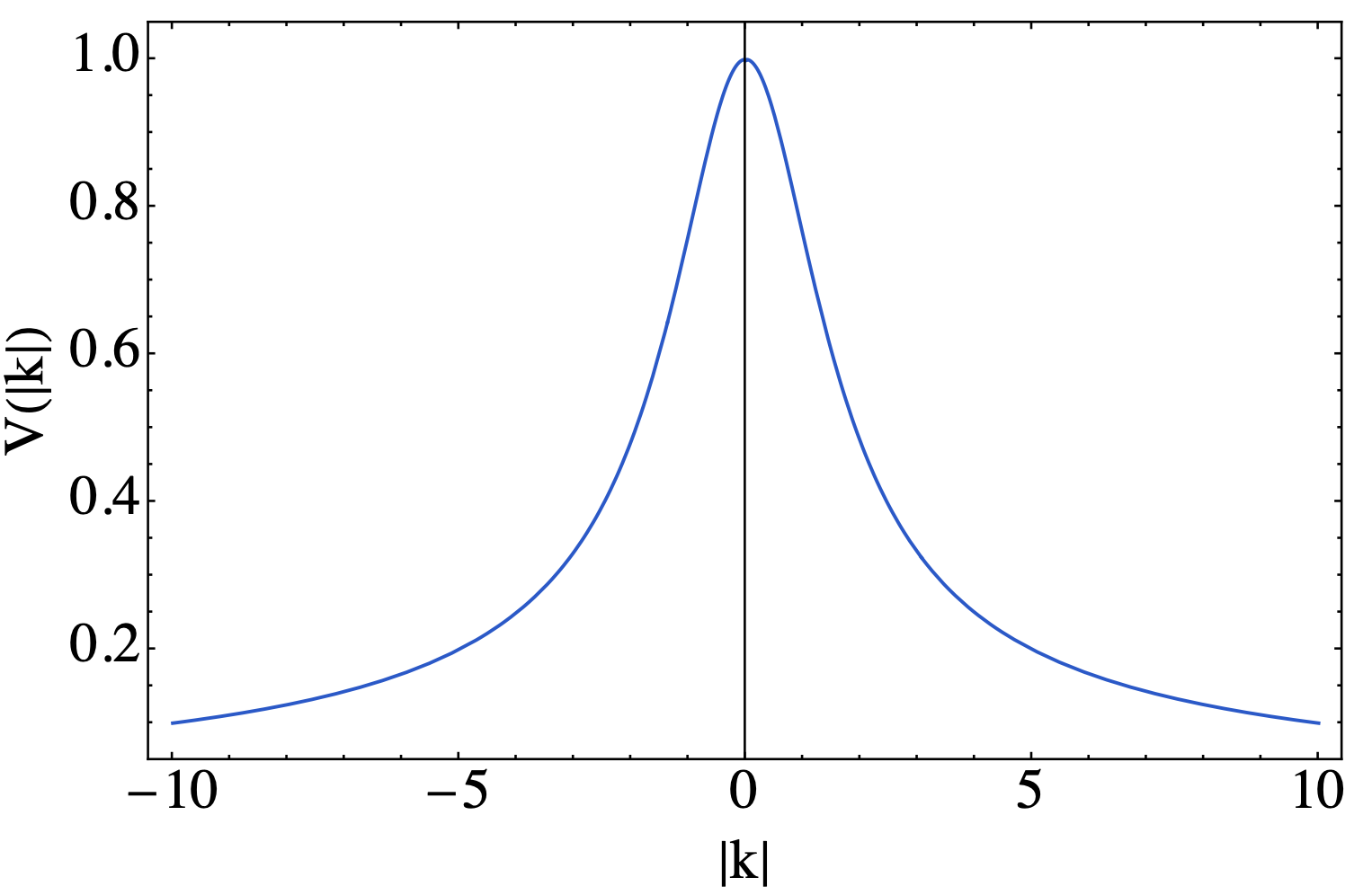
在固体理论和量子场论的学习过程中都遇到了电极化函数的计算,在这里就详细的整理一下如何计算电子气中的电极化函数,这个计算有时候也成为RPA,当然这个方法并不仅限于计算电极化,还可以用来计算其它的一些量。{:.info} 运动方程方法推导假设在系统中放入一个杂质点电荷$\rho_i(\mathbf{r},t)$或这其傅里叶变换形式为$\rho_i(\mathbf{q},\omega)$,那么有这个电荷产生的等效势为$V_i(\mathbf{q},\omega)=-e\phi_i(\mathbf{q},\omega)$.一旦存在了杂质电荷之后,那么在其周围就会形成屏蔽电荷,从而也会产生一个额外的屏蔽势$V_s(\mathbf{q},\omega)$,则可以由一下方程 V(\mathbf{q},\omega)=V_i(\mathbf{q},\omega)+V_s(\mathbf{q},\omega)\nabla^2V_s(\mathbf{r},t)=4\pi e\rho_s(\mathbf{r},t)\qquad or\qquad V_s(\mathbf{q},\omega)=-\frac{4\pi e}{q^2}\rho_s(\mathbf{q},\omega)\nabla^2 V_i(\mathbf{r},t)=4\pi e\rho_i(\mathbf{r},t)\qquad or\qquad V_s(\mathbf{q},\omega)=-\frac{4\pi e}{q^2}\rho_i(\mathbf{q},\omega)综上所述,可以知道由杂质电荷引起的势$V_i$是可以知道的,但是电子感受到的应该是$V(\mathbf{q},\omega)$,所以最终的问题就是如何求解这个总的势能,从而可以得到电极化函数 \epsilon(\mathbf{q},\omega)=\frac{V_i(\mathbf{q},\omega)}{V(\mathbf{q},\omega)}电子的有效哈密顿量为 H=\sum_{\mathbf{p}\sigma}\epsilon_\mathbf{p}...
松原频率求和
在学习格林函数的过程中,松原格林函数用来计算是很方便的,虽然它是用来处理有限温的问题,但是通过解析延拓之后,和零温下的格林函数的结果是相同的,而且相对于零温格林函数的计算,松原格林函数涉及到松原频率求和,在计算上面我觉得还是具有一定的简便性的,只需要扎实的掌握粒子分布函数和复变函数的留数定理之后,就可以快速的进行计算。{:.info} 留数定理设区域G的边界C为以分段光滑的简单闭合曲线,若除有限个孤立奇点$b_k,(k=1,2,3,…,n)$外,函数$f(z)$在G内单值解析,在G上连续,并且在C上$f(z)$没有奇点,则$\int_Cf(z)dz=2\pi i\sum_{k=1}^nRes[f(b_k)]$,$Res[f(b_k)]$即为函数$f(z)$在$b_k$处的留数,它等于$f(z)$在$b_k$的邻域内洛朗展开 f(z)=\sum_{l=-\infty}^{\infty}a^{(k)}_l(z-b_k)^l中$(z-b_k)^{-1}$的系数$a_{-1}^{(k)}$。 留数计算理解假设$z=b$是函数的一阶极点,则有$f(z)=a_1(z-b)^{-1}+a_0+a_1(z-b)+a_2(a-b)^2+…$,那么函数$f(z)$在$z=b$上的留数为$a_{-1}=lim_{z\rightarrow b}(z-b)f(z)$。从形式上来看,留数的计算就是在原函数$f(z)$中,将这个极点$z=b$抠去$(z-b)f(z)$,剩下的部分取$z=b$时候的值,就是这个函数在该奇点处的留数,这个简单的方法只是对于一阶极点而言,如果是高阶的极点,比如$z=b$是函数$f(z)$的$m$阶极点,则系数a_{-1}=\frac{1}{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}(z-b)^mf(z)|_{z=b}。 如果$z=b$是$f(z)$的一阶极点,结社函数$f(z)$可以表示为$\frac{P(z)}{Q(z)}$,$P(z),Q(z)$在$b$点及其邻域内解析,$z=b$是$Q(z)$的一阶零点,$Q(b)=0,Q’(z)\neq0,P(b)\neq0$,则可以得到$a_{-1}=\lim_{z\rightarrow b}(z-b)f(z)=\lim_{z\rightarrow...
SSH model的Winding Number计算
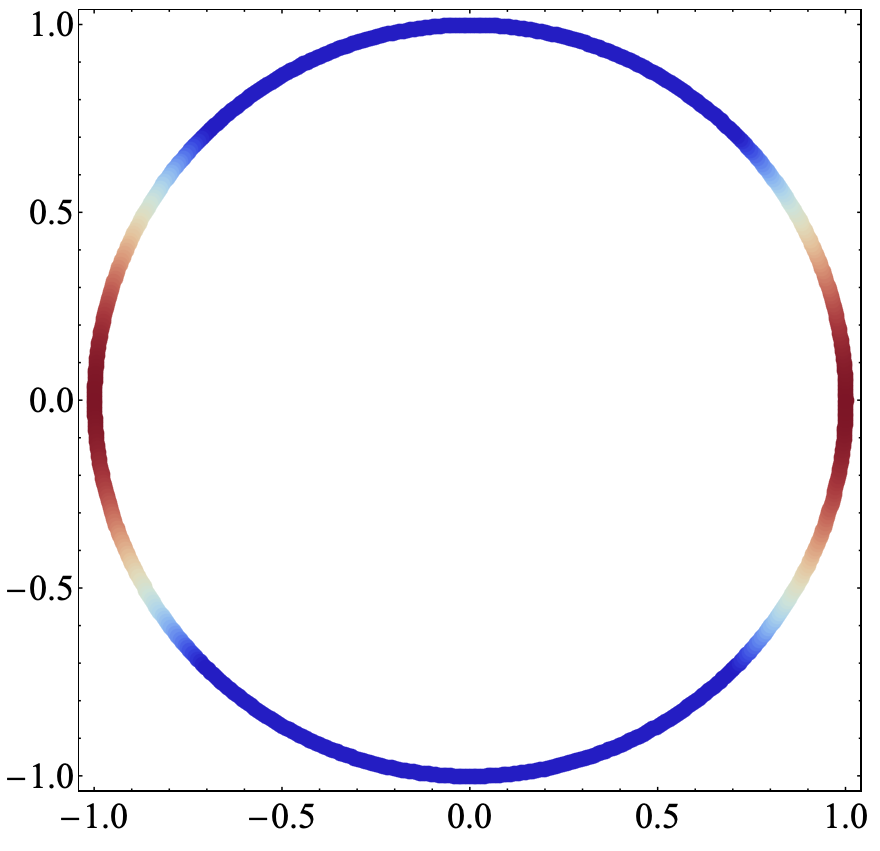
在这篇博客中通过简单的SSH模型,来计算一下Winding Number这一拓扑不变量。虽然这个模型很简单,但是最近在学习Non-Hermitian的文章中,很多都是以这个模型为基础,研究非厄米体系的一些基本性质,其中也有通过计算非厄米系统的Winding Number来联系体系的拓扑性质。这里我就暂时不涉及非厄米的内容,因为我也只是对这个课题了解一点点内容,这里主要计算厄密SSH模型的Winding Number。{:.info} Winding Number直观描述Winding number是指平面一条闭合的曲线以逆时针方向绕一点所转的圈数,正方向是逆时针,则这时候的Winding number是正数,如果是顺时针方向绕动的,那么Winding number就是负数. 数学表达平面上的曲线可以通过参数方程来表示 x=x(t) \text { and } y=y(t) \quad \text { for } 0 \leq t \leq 1如果在$t=0$和$t=1$的时候位置是相同的,那么在参数$t$变化的过程中就形成了一个闭合的曲线.这个问题同样可以放在极坐标空间中来处理 r=r(t) \text { and } \theta=\theta(t) \quad \text { for } 0 \leq t \leq 1根据前面的假设,$t=0$与$t=1$位置相同,构成一个闭合的曲线,那么在极坐标空间中$\theta(0)$与$\theta(1)$之间则相差$2\pi$的整数倍 \text { winding number }=\frac{\theta(1)-\theta(0)}{2 \pi}再次转换坐标系,在复平面上进行分析,直角平面上的两个分量分别看作是复平面上的实部和虚部,$z=x+\text{i} y=re^{i\theta}$ d z=e^{i \theta} d r+i r e^{i \theta} d \theta\frac{d z}{z}=\frac{d r}{r}+i d \theta=d[\ln r]+i d \theta由于$\gamma$是闭合曲线,那么总的$\ln(r)$的改变等于0,所以积分$\frac{dz}{z}$就是i乘以总的$\theta$角的改变值,所以Winding...
通过Wannier Center计算体系$Z_2$拓扑不变量
在$Z_2$拓扑不变量计算中,是通过一个比较直接的数值计算方法来对系统的$Z_2$拓扑不变量进行计算,而在学习能带拓扑的时候,最基本的理解都是通过电荷极化以及Wannier函数进行的,所以这里再利用Wannier Center的方法来计算体系的$Z_2$拓扑不变量,通过这个方法计算的时候,可以建立一个很清晰的物理图像,从而可以进一步加深对凝聚态物理中的拓扑有更深的理解。{:.info} Wannier Center在学习在利用Wannier Center计算拓扑不变量的过程中,我想先对参考文章中的一些概念再做一些自己的理解。 Bloch Function在周期势场中运动的电子,其波函数满足Bloch定理$\psi(\mathbf{r})=e^{i\mathbf{k}\mathbf{r}}u(\mathbf{r})$,其中$e^{i\mathbf{k}\mathbf{r}}$是调幅因子,而$u(\mathbf{r})$是函数的周期部分,即这一项就是满足和势场相同的周期性,也可以说这一项就是一个元胞内的波函数(cell function)。$u(\mathbf{r}+\mathbf{R})=u(\mathbf{r})$。 Wannier Function在学习固体物理的时候,与Bloch函数相对应的就是Wannier函数,其中Bloch函数是个拓展性非常好的波函数,而相反的Wannier函数则是一个局域性非常强的波函数,其实这一点可以通过它们之间的联系看出来,因为它们二者之间互为其Fourier变化。那么通过量子力学中的动量空间与实空间的对应关系,自然也就可以有这一个清晰的图像对应。这里再强调一下Wannier函数的重要性,我在学习凝聚态拓扑的过程中了解到,很多电荷极化以及现代极化理论的理解和计算都离不开对Wannier函数。Bloch函数与Wannier函数之间的联系为: |k\alpha\tau\rangle=\frac{1}{\sqrt{N_{cell}}}\sum_je^{ik(R_j+\tau})|j\alpha\tau\rangleBloch函数和Wannier函数都是完备基矢,都可以用作基矢来对任意的波函数进行展开,只要选取合适的展开系数即可 位置算符文中首先定义了一个位置算符$\hat{X}=\sum_{j a \tau}...
$Z_2$拓扑不变量计算
前面学习了chern数的计算,其中其实遇到了波函数规范选择的问题,这个在计算时间反演不变系统的$Z_2$拓扑不变量的时候也会遇到,暂时我对这个规范问题也没有很好的理解,正好也通过计算$Z_2$拓扑不变量来对规范问题进行更进一步的了解,这里只是单纯的学习如何计算$Z_2$。{:.info} 计算方法首先介绍一下我学习的计算$Z_2$ 拓扑不变量的方法,主要参考了这个PPT中的计算方法。如果网址打不开,可以在这里下载。我在这里只是简单的展示一下如何用代码计算拓扑不变量,而对于ppt中的计算方法还在进一步理解中,也非常欢迎对这方面比较熟悉的人,可以和我交流交流,让我对这部分内容有一个更加深入的了解。 BHZ 模型$Z_2$拓扑不变量计算在这里,我就一比较熟悉的BHZ模型为例,来计算一下其$Z_2$拓扑不变量。在这里首先对ppt中的公式运用做一些说明。 首先,熟悉chern number计算的话,肯定知道我们是要对占据态能带进行拓扑不变量的计算,在第10张ppt中 U_{\mu}=\det(\langle u_m(\mathbf{k})|u_n(\mathbf{k} + \Delta\mu)\rangle)这里的$|u\rangle$代表的都是占据态的本征矢量,所以如果求解得到哈密顿量对应的本征值和本征矢量后,假设此时化学势为0,那么应该选取的就是能量小于零对应的本征矢量来进行计算。这里因为是存在时间反演对称,所以如果本征值一定会成对出现,即存在简并态(两个本征矢量具有相同的本征值),关于相同的本征值有两个,这一点可以在计算的时候明确得到。 假设计算得到一个本征值为$E_1$,那么对应的一定存在另外一个本征值$E_2$,满足$E_1 = E_2$,但是这两个本征值对应的本征矢量是不同的。所以上面的表达式中计算的矩阵行列式,这个矩阵就是由这两个简并的本征态构成的。而$\Delta \mu$则是代表在$k_x$或者$k_y$方向上有一个增量。我在看ppt中的这个行列式计算的公式的时候,是觉得它有一些让人疑惑的地方。还是以第十张ppt中的计算公式$U_{\mu}=\det(\langle u_m(\mathbf{k})|u_n(\mathbf{k}...