反铁磁涨落与超导序参量的关系
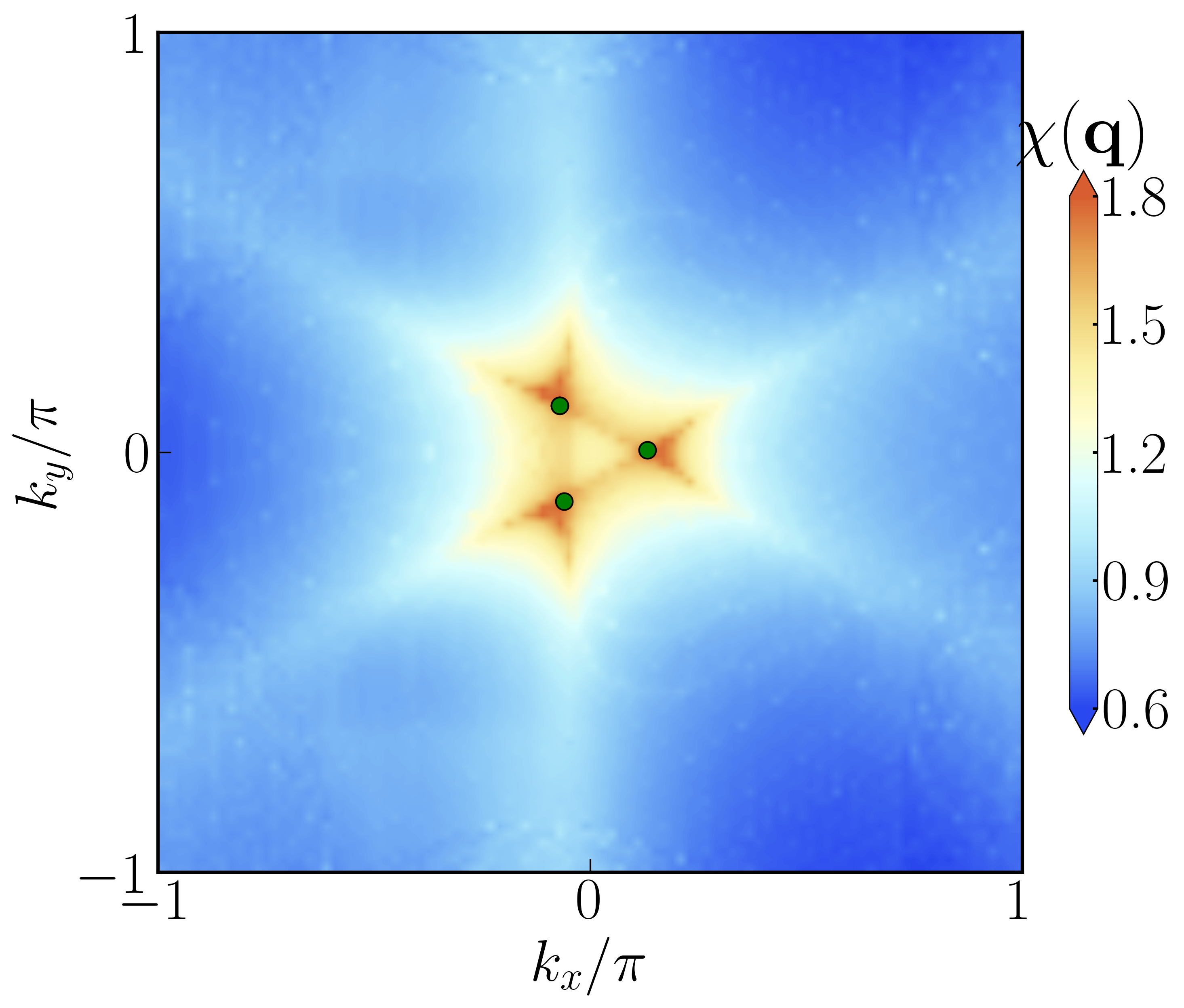
首先说一个结论:在弱耦合 RPA 框架中,由nesting 矢量$\boldsymbol{q}$相连接的两个费米面上的序参量必然反号,这里就来详细的解释说明一下。 首先,在 RPA 这个框架中...
Pauli 极限
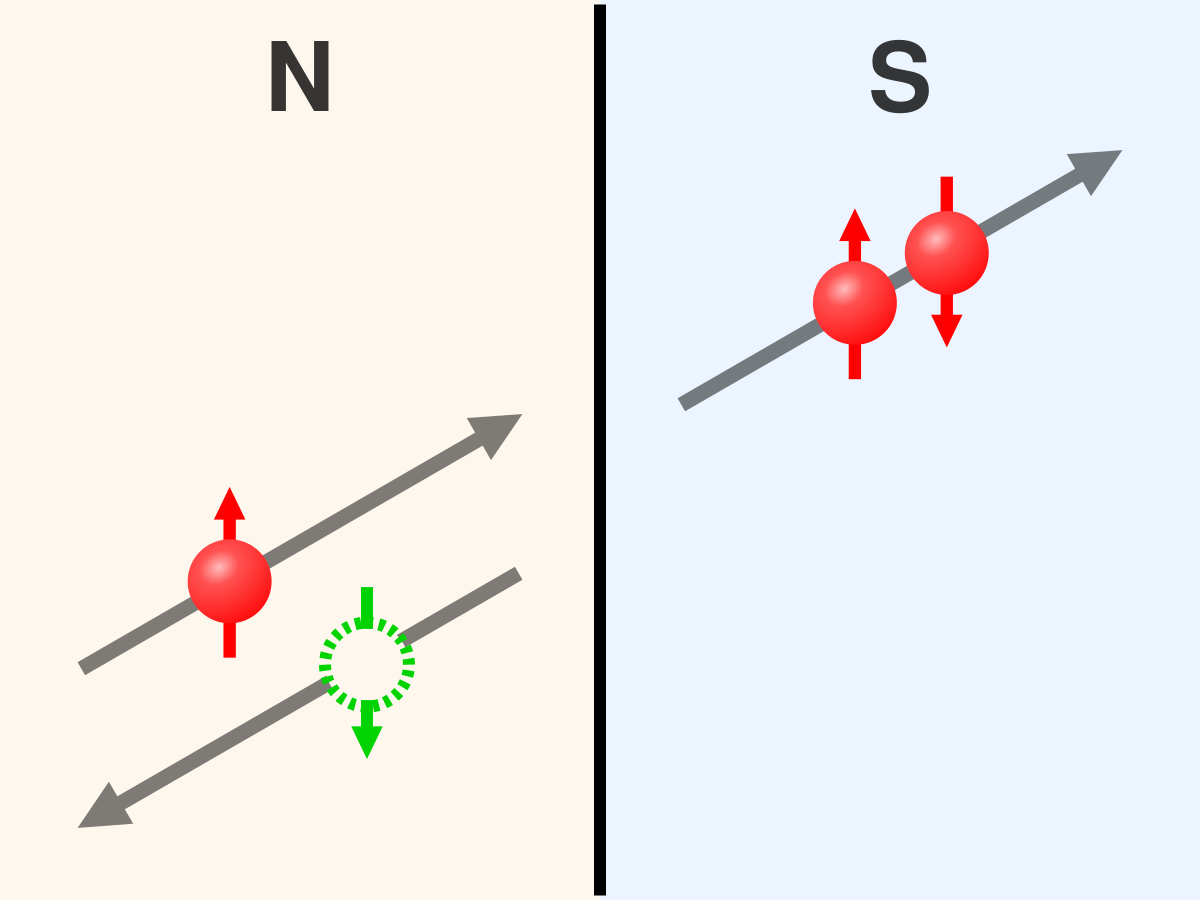
该Blog 通过自由能方式推导普通 BCS 超导体的 Pauli 极限 Pauli极限磁场与自旋单重态超导显然是不兼容的,但是在满足什么条件下可以磁场会破坏超导,这里通过自由能的方式来推导一下...
Ward-Takahashi 恒等式
Ward-Takahashi 恒等式是连续对称性(如规范对称性)在量子场论中的必然结果。它们以关联函数间必须满足的数学关系的形式,确保了量子理论在微扰展开的任意阶都严格地保持其对称性,是连接经典...
响应函数的奇偶性
在很多物理量的分析中,都需要用到关联函数,这里从定义上来分析一下关联函数实部和虚部的奇偶性。 推迟格林函数的奇偶性分析对于推迟格林函数,其定义为 \Pi^R(t) = -i\Theta(t)...
晶格规范与原子规范
在构建紧束缚模型的时候,不同规范的选择会对后续物理量的计算有影响,该 Blog 简单整理关于原子规范和晶格规范的对比。 晶格规范与原子规范 晶格规范(Periodic gauge / lat...
Mathematica一些小技巧收集
整理收集一下使用Mathematica时候的一些小技巧 快速获取等高线数据利用Mathematica绘制费米面最简单高效的方式就是使用ContourPlot函数,通过快速获取这些等能线上的点就...









![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

