Yu-Xuan's Blog

本笔记详细推导了downfolding方法得到有效哈密顿量的过程 Downfolding 方法推导有效哈密顿量1. 问题描述考虑一个分块矩阵形式的哈密顿量 H = \begin{pmatri...

拖着疲惫的身体回到了广州，都说旅行是花钱找罪受，虽然自己不那么认为，但是身体是这么告诉我的。 计划一转眼，就到了四月份，过的平平淡淡，也没有收获，虽然在寒假完成了老师交代的东西，转眼又是一个...

将看到的Fortran中常用的一些语法记录起来，方便查阅。 Fortran中常用的库函数总结1. Cheevd 厄密矩阵本征值与本征矢的求解 2. getrf,getri getrf 对一...

最近准备仔细学习一遍群论，平时学习也喜欢结合计算机，这样对一些概念的理解可以更加透彻一些。恰好又找到了一本群论的书，且完全是利用Mathematica来对群论的概念进行讲解，正好在这里整理一下自...

在学习Berry位相与电荷极化的过程中,总算是成功的理解了便面电荷密度和电荷极化之间的联系,以及表面电荷的多值问题,这里就把自己的一些理解和写的一些代码整理出来,也加深一下自己对这个概念的理解....

打卡11月的第一个任务,在前面的博客中提到过计算拓扑不变量的问题,利用Wilson Loop的方法可以很好的将规范选择问题避免,最近正好在看一篇高阶拓扑半金属的文章,正好学习一下如何利用Wils...

前面有两篇博客主要关注的不同的基矢下如何构建BdG形式的哈密顿量,既然只不过是基矢的变化,那么两个哈密顿量肯定就是等价的,这里就给一个具体的实例,来看看怎么把两个不同基矢下的哈密顿量进行相互的改...

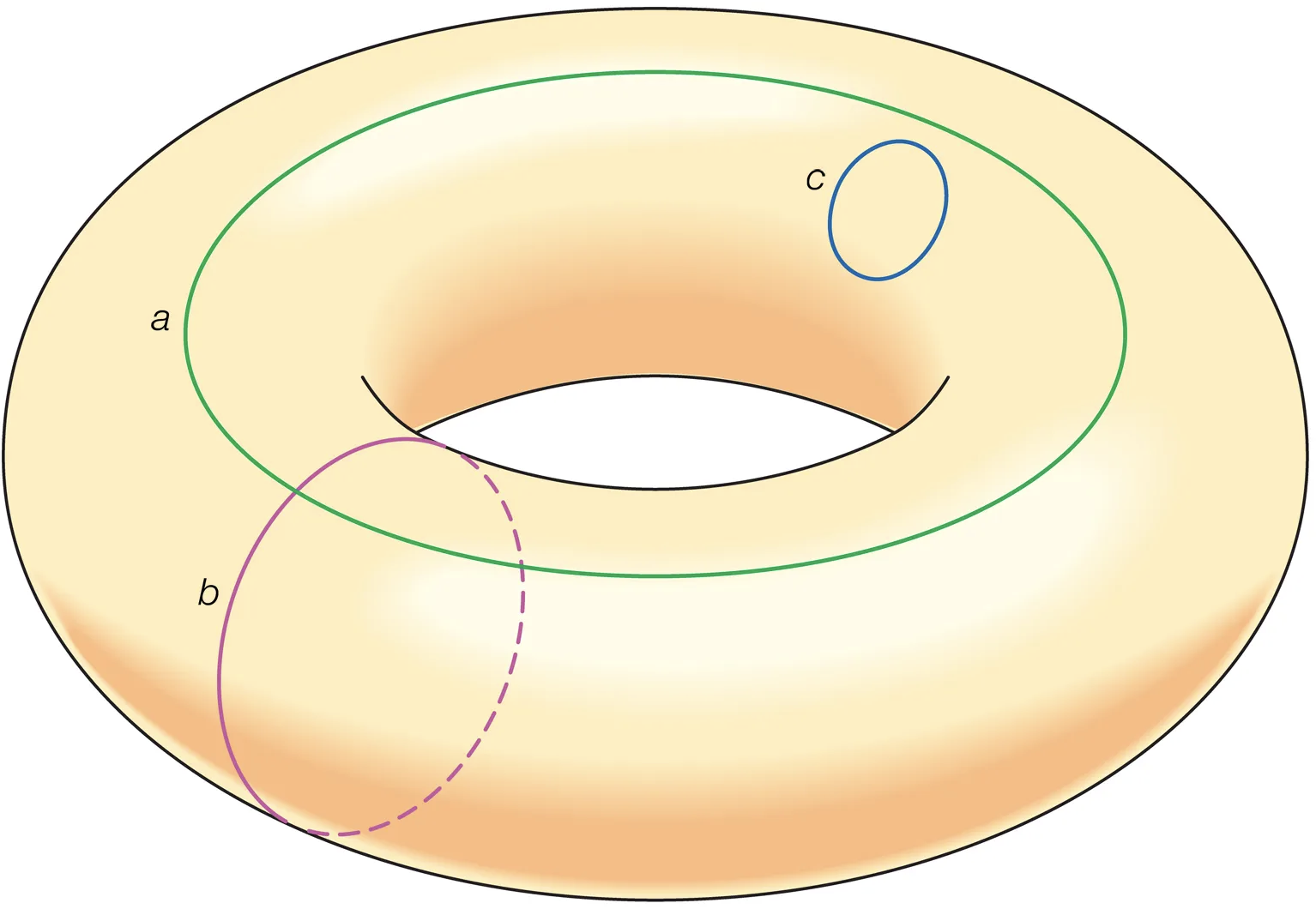
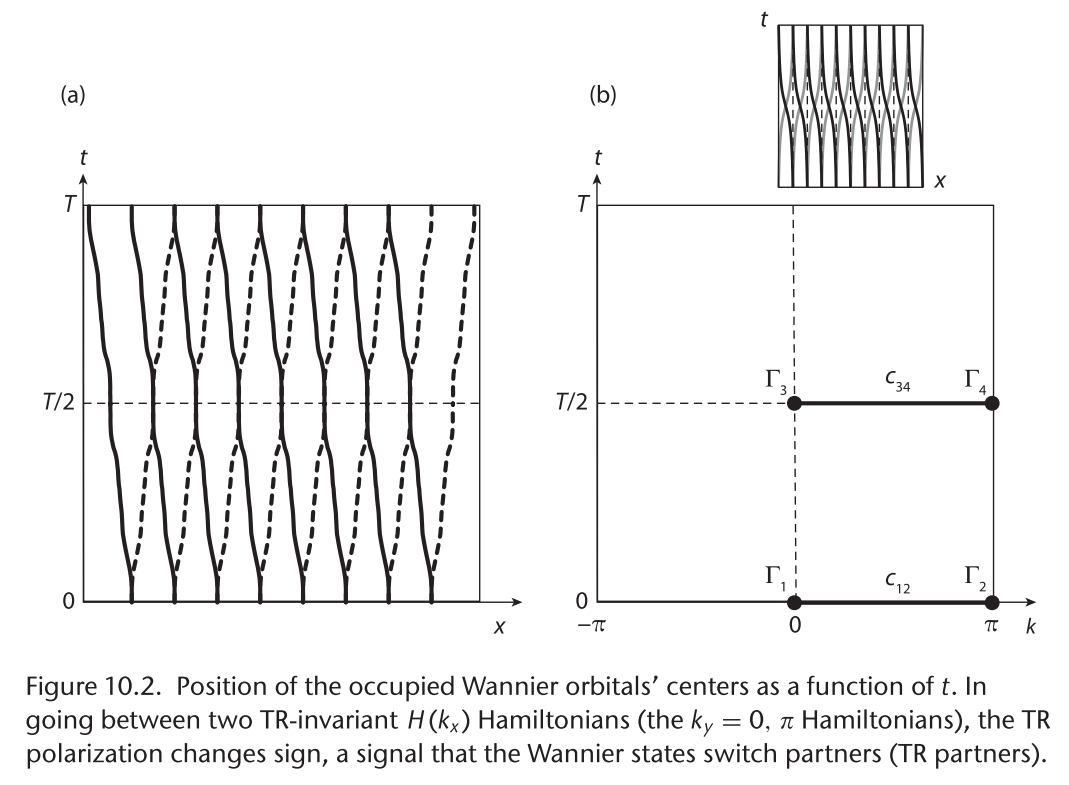
满足时间反演不变的体系, Chern数为0, 但是可以通过$Z_2$拓扑不变量描述, 任然可以通过一个物理图像来理解这个不变量和某一种极化之间的对应关系, 这里整理一下时间反演极化与$Z_2$拓...

在这里主要整理记录一些平时在推导中可能会用到的一些公式，以及在做计算时遇到的一些小技巧，因为时间长了可能对细节问题会忘记，所以整理在这里也可以很方便的进行查阅，同时在整理的过程中也是自己对这些知...